Andrew Bray
The Test of Tests: A Framework For Differentially Private Hypothesis Testing
Feb 08, 2023Abstract:We present a generic framework for creating differentially private versions of any hypothesis test in a black-box way. We analyze the resulting tests analytically and experimentally. Most crucially, we show good practical performance for small data sets, showing that at epsilon = 1 we only need 5-6 times as much data as in the fully public setting. We compare our work to the one existing framework of this type, as well as to several individually-designed private hypothesis tests. Our framework is higher power than other generic solutions and at least competitive with (and often better than) individually-designed tests.
Improved Differentially Private Analysis of Variance
Mar 01, 2019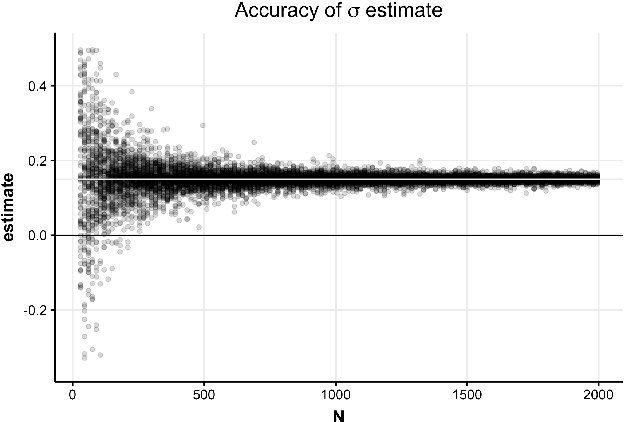
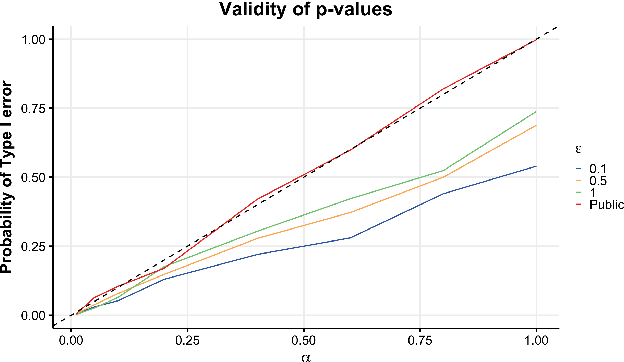
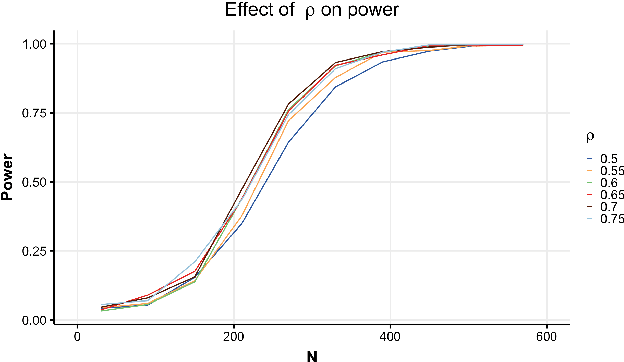
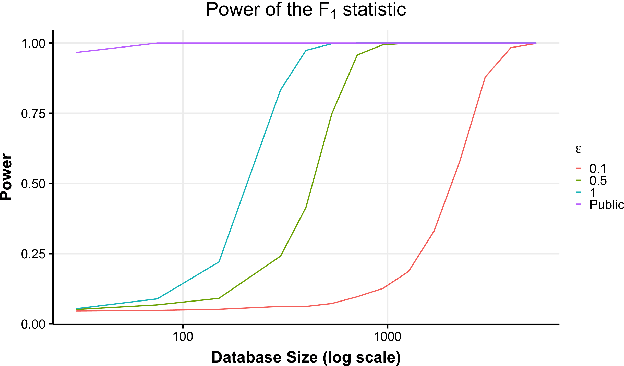
Abstract:Hypothesis testing is one of the most common types of data analysis and forms the backbone of scientific research in many disciplines. Analysis of variance (ANOVA) in particular is used to detect dependence between a categorical and a numerical variable. Here we show how one can carry out this hypothesis test under the restrictions of differential privacy. We show that the $F$-statistic, the optimal test statistic in the public setting, is no longer optimal in the private setting, and we develop a new test statistic $F_1$ with much higher statistical power. We show how to rigorously compute a reference distribution for the $F_1$ statistic and give an algorithm that outputs accurate $p$-values. We implement our test and experimentally optimize several parameters. We then compare our test to the only previous work on private ANOVA testing, using the same effect size as that work. We see an order of magnitude improvement, with our test requiring only 7% as much data to detect the effect.
A Differentially Private Wilcoxon Signed-Rank Test
Sep 05, 2018



Abstract:Hypothesis tests are a crucial statistical tool for data mining and are the workhorse of scientific research in many fields. Here we present a differentially private analogue of the classic Wilcoxon signed-rank hypothesis test, which is used when comparing sets of paired (e.g., before-and-after) data values. We present not only a private estimate of the test statistic, but a method to accurately compute a p-value and assess statistical significance. We evaluate our test on both simulated and real data. Compared to the only existing private test for this situation, that of Task and Clifton, we find that our test requires less than half as much data to achieve the same statistical power.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge