Multiaccurate Proxies for Downstream Fairness

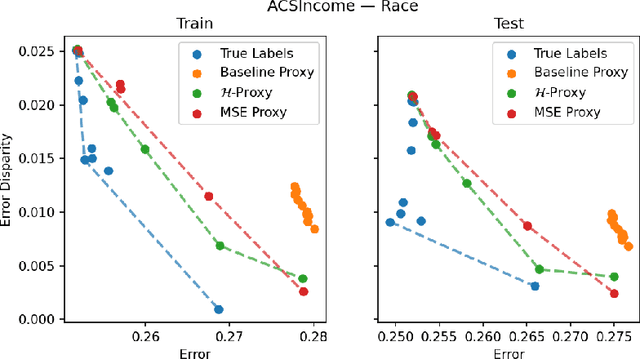
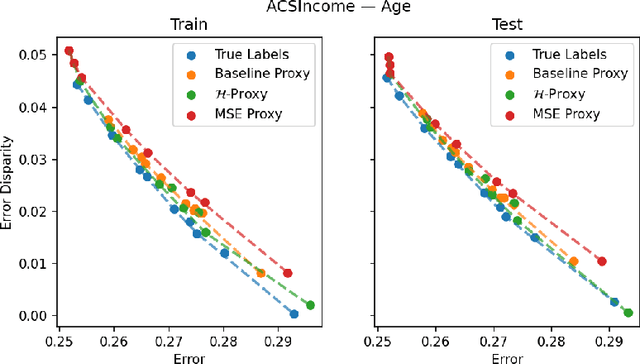
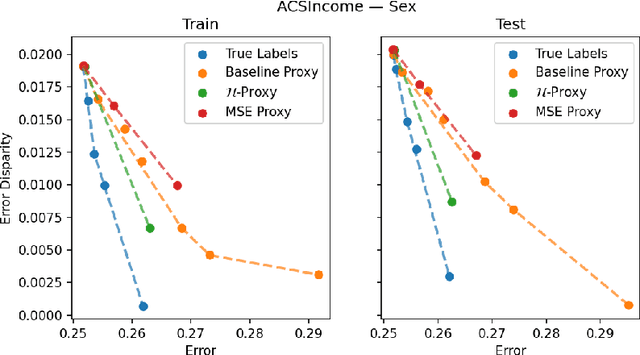
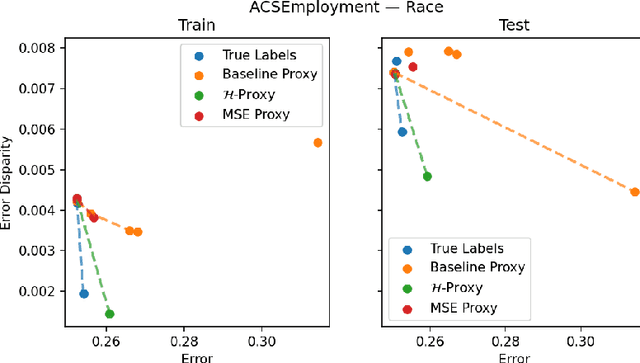
We study the problem of training a model that must obey demographic fairness conditions when the sensitive features are not available at training time -- in other words, how can we train a model to be fair by race when we don't have data about race? We adopt a fairness pipeline perspective, in which an "upstream" learner that does have access to the sensitive features will learn a proxy model for these features from the other attributes. The goal of the proxy is to allow a general "downstream" learner -- with minimal assumptions on their prediction task -- to be able to use the proxy to train a model that is fair with respect to the true sensitive features. We show that obeying multiaccuracy constraints with respect to the downstream model class suffices for this purpose, and provide sample- and oracle efficient-algorithms and generalization bounds for learning such proxies. In general, multiaccuracy can be much easier to satisfy than classification accuracy, and can be satisfied even when the sensitive features are hard to predict.

Lexicographically Fair Learning: Algorithms and Generalization

We extend the notion of minimax fairness in supervised learning problems to its natural conclusion: lexicographic minimax fairness (or lexifairness for short). Informally, given a collection of demographic groups of interest, minimax fairness asks that the error of the group with the highest error be minimized. Lexifairness goes further and asks that amongst all minimax fair solutions, the error of the group with the second highest error should be minimized, and amongst all of those solutions, the error of the group with the third highest error should be minimized, and so on. Despite its naturalness, correctly defining lexifairness is considerably more subtle than minimax fairness, because of inherent sensitivity to approximation error. We give a notion of approximate lexifairness that avoids this issue, and then derive oracle-efficient algorithms for finding approximately lexifair solutions in a very general setting. When the underlying empirical risk minimization problem absent fairness constraints is convex (as it is, for example, with linear and logistic regression), our algorithms are provably efficient even in the worst case. Finally, we show generalization bounds -- approximate lexifairness on the training sample implies approximate lexifairness on the true distribution with high probability. Our ability to prove generalization bounds depends on our choosing definitions that avoid the instability of naive definitions.

Convergent Algorithms for (Relaxed) Minimax Fairness

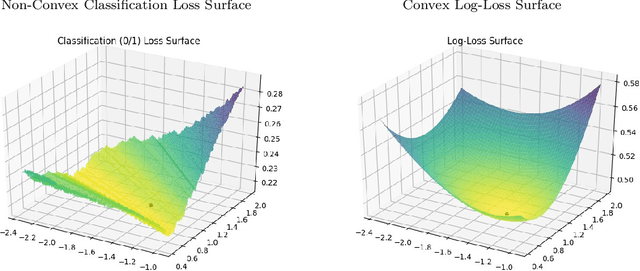
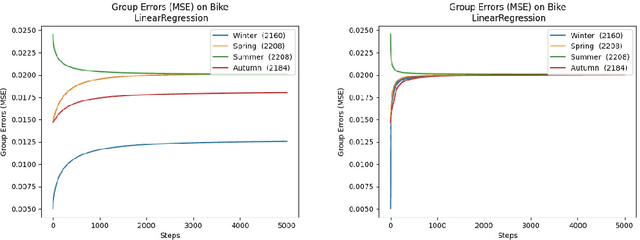
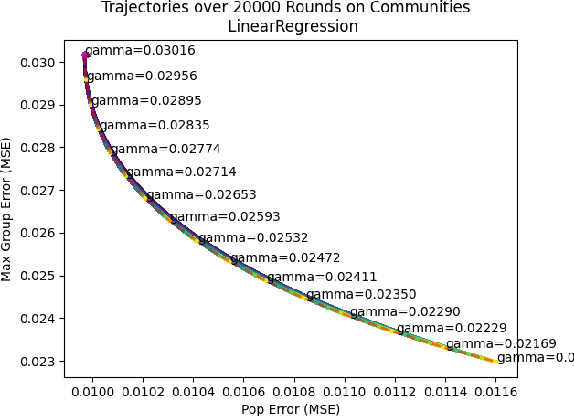
We consider a recently introduced framework in which fairness is measured by worst-case outcomes across groups, rather than by the more standard $\textit{difference}$ between group outcomes. In this framework we provide provably convergent $\textit{oracle-efficient}$ learning algorithms (or equivalently, reductions to non-fair learning) for $\textit{minimax group fairness}$. Here the goal is that of minimizing the maximum loss across all groups, rather than equalizing group losses. Our algorithms apply to both regression and classification settings and support both overall error and false positive or false negative rates as the fairness measure of interest. They also support relaxations of the fairness constraints, thus permitting study of the tradeoff between overall accuracy and minimax fairness. We compare the experimental behavior and performance of our algorithms across a variety of fairness-sensitive data sets and show cases in which minimax fairness is strictly and strongly preferable to equal outcome notions, in the sense that equal outcomes can only be obtained by artificially inflating the harm inflicted on some groups compared to what they suffer under the minimax solution.