Convergent Algorithms for (Relaxed) Minimax Fairness

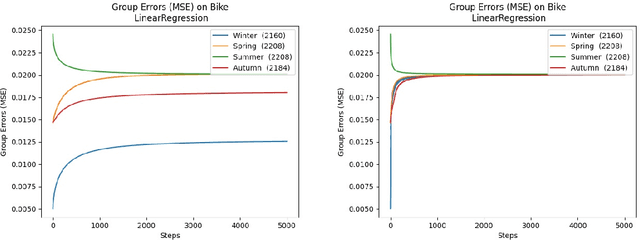
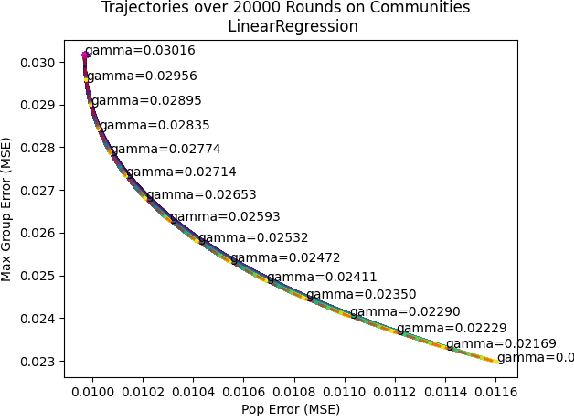
We consider a recently introduced framework in which fairness is measured by worst-case outcomes across groups, rather than by the more standard $\textit{difference}$ between group outcomes. In this framework we provide provably convergent $\textit{oracle-efficient}$ learning algorithms (or equivalently, reductions to non-fair learning) for $\textit{minimax group fairness}$. Here the goal is that of minimizing the maximum loss across all groups, rather than equalizing group losses. Our algorithms apply to both regression and classification settings and support both overall error and false positive or false negative rates as the fairness measure of interest. They also support relaxations of the fairness constraints, thus permitting study of the tradeoff between overall accuracy and minimax fairness. We compare the experimental behavior and performance of our algorithms across a variety of fairness-sensitive data sets and show cases in which minimax fairness is strictly and strongly preferable to equal outcome notions, in the sense that equal outcomes can only be obtained by artificially inflating the harm inflicted on some groups compared to what they suffer under the minimax solution.