Minimax Group Fairness in Strategic Classification

In strategic classification, agents manipulate their features, at a cost, to receive a positive classification outcome from the learner's classifier. The goal of the learner in such settings is to learn a classifier that is robust to strategic manipulations. While the majority of works in this domain consider accuracy as the primary objective of the learner, in this work, we consider learning objectives that have group fairness guarantees in addition to accuracy guarantees. We work with the minimax group fairness notion that asks for minimizing the maximal group error rate across population groups. We formalize a fairness-aware Stackelberg game between a population of agents consisting of several groups, with each group having its own cost function, and a learner in the agnostic PAC setting in which the learner is working with a hypothesis class H. When the cost functions of the agents are separable, we show the existence of an efficient algorithm that finds an approximately optimal deterministic classifier for the learner when the number of groups is small. This algorithm remains efficient, both statistically and computationally, even when H is the set of all classifiers. We then consider cost functions that are not necessarily separable and show the existence of oracle-efficient algorithms that find approximately optimal randomized classifiers for the learner when H has finite strategic VC dimension. These algorithms work under the assumption that the learner is fully transparent: the learner draws a classifier from its distribution (randomized classifier) before the agents respond by manipulating their feature vectors. We highlight the effectiveness of such transparency in developing oracle-efficient algorithms. We conclude with verifying the efficacy of our algorithms on real data by conducting an experimental analysis.

Reconciling Heterogeneous Effects in Causal Inference

In this position and problem pitch paper, we offer a solution to the reference class problem in causal inference. We apply the Reconcile algorithm for model multiplicity in machine learning to reconcile heterogeneous effects in causal inference. Discrepancy between conditional average treatment effect (CATE) estimators of heterogeneous effects poses the reference class problem, where estimates for individual predictions differ by choice of reference class. By adopting the individual to group framework for interpreting probability, we can recognize that the reference class problem -- which appears across fields such as philosophy of science and causal inference -- is equivalent to the model multiplicity problem in computer science. We then apply the Reconcile Algorithm to reconcile differences in estimates of individual probability among CATE estimators. Because the reference class problem manifests in contexts of individual probability prediction using group-based evidence, our results have tangible implications for ensuring fair outcomes in high-stakes such as healthcare, insurance, and housing, especially for marginalized communities. By highlighting the importance of mitigating disparities in predictive modeling, our work invites further exploration into interdisciplinary strategies that combine technical rigor with a keen awareness of social implications. Ultimately, our findings advocate for a holistic approach to algorithmic fairness, underscoring the critical role of thoughtful, well-rounded solutions in achieving the broader goals of equity and access.

Balanced Filtering via Non-Disclosive Proxies

We study the problem of non-disclosively collecting a sample of data that is balanced with respect to sensitive groups when group membership is unavailable or prohibited from use at collection time. Specifically, our collection mechanism does not reveal significantly more about group membership of any individual sample than can be ascertained from base rates alone. To do this, we adopt a fairness pipeline perspective, in which a learner can use a small set of labeled data to train a proxy function that can later be used for this filtering task. We then associate the range of the proxy function with sampling probabilities; given a new candidate, we classify it using our proxy function, and then select it for our sample with probability proportional to the sampling probability corresponding to its proxy classification. Importantly, we require that the proxy classification itself not reveal significant information about the sensitive group membership of any individual sample (i.e., it should be sufficiently non-disclosive). We show that under modest algorithmic assumptions, we find such a proxy in a sample- and oracle-efficient manner. Finally, we experimentally evaluate our algorithm and analyze generalization properties.

Correcting Underrepresentation and Intersectional Bias for Fair Classification

We consider the problem of learning from data corrupted by underrepresentation bias, where positive examples are filtered from the data at different, unknown rates for a fixed number of sensitive groups. We show that with a small amount of unbiased data, we can efficiently estimate the group-wise drop-out parameters, even in settings where intersectional group membership makes learning each intersectional rate computationally infeasible. Using this estimate for the group-wise drop-out rate, we construct a re-weighting scheme that allows us to approximate the loss of any hypothesis on the true distribution, even if we only observe the empirical error on a biased sample. Finally, we present an algorithm encapsulating this learning and re-weighting process, and we provide strong PAC-style guarantees that, with high probability, our estimate of the risk of the hypothesis over the true distribution will be arbitrarily close to the true risk.

Multiaccurate Proxies for Downstream Fairness

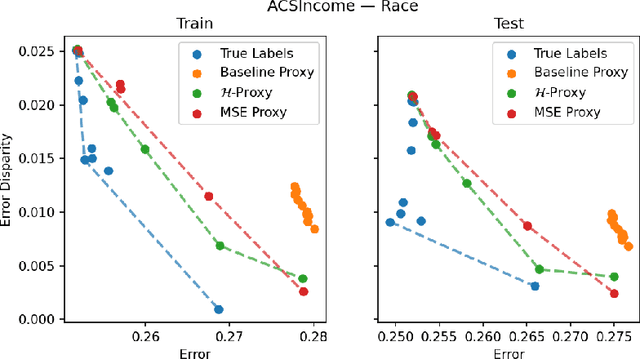
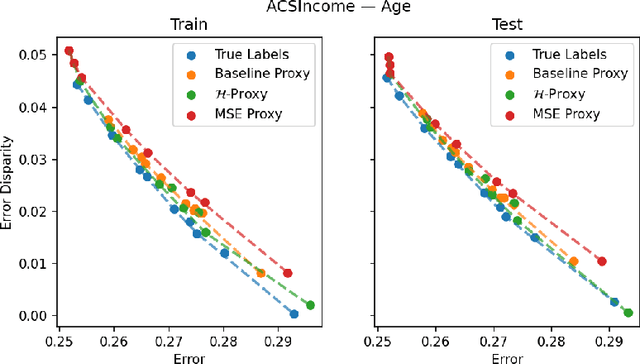
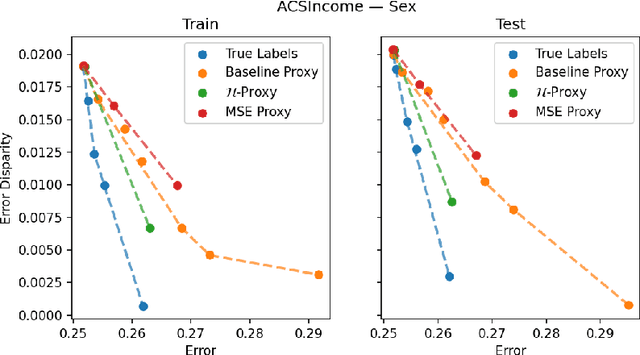
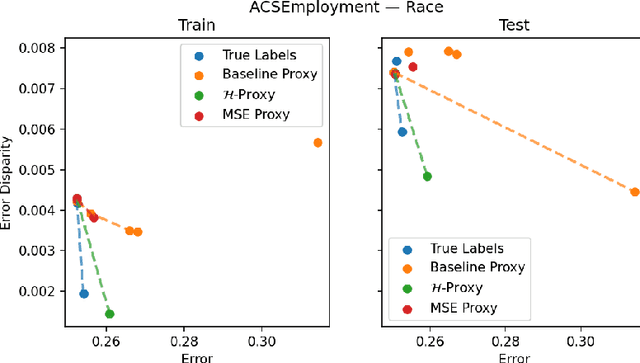
We study the problem of training a model that must obey demographic fairness conditions when the sensitive features are not available at training time -- in other words, how can we train a model to be fair by race when we don't have data about race? We adopt a fairness pipeline perspective, in which an "upstream" learner that does have access to the sensitive features will learn a proxy model for these features from the other attributes. The goal of the proxy is to allow a general "downstream" learner -- with minimal assumptions on their prediction task -- to be able to use the proxy to train a model that is fair with respect to the true sensitive features. We show that obeying multiaccuracy constraints with respect to the downstream model class suffices for this purpose, and provide sample- and oracle efficient-algorithms and generalization bounds for learning such proxies. In general, multiaccuracy can be much easier to satisfy than classification accuracy, and can be satisfied even when the sensitive features are hard to predict.

Lexicographically Fair Learning: Algorithms and Generalization

We extend the notion of minimax fairness in supervised learning problems to its natural conclusion: lexicographic minimax fairness (or lexifairness for short). Informally, given a collection of demographic groups of interest, minimax fairness asks that the error of the group with the highest error be minimized. Lexifairness goes further and asks that amongst all minimax fair solutions, the error of the group with the second highest error should be minimized, and amongst all of those solutions, the error of the group with the third highest error should be minimized, and so on. Despite its naturalness, correctly defining lexifairness is considerably more subtle than minimax fairness, because of inherent sensitivity to approximation error. We give a notion of approximate lexifairness that avoids this issue, and then derive oracle-efficient algorithms for finding approximately lexifair solutions in a very general setting. When the underlying empirical risk minimization problem absent fairness constraints is convex (as it is, for example, with linear and logistic regression), our algorithms are provably efficient even in the worst case. Finally, we show generalization bounds -- approximate lexifairness on the training sample implies approximate lexifairness on the true distribution with high probability. Our ability to prove generalization bounds depends on our choosing definitions that avoid the instability of naive definitions.

Convergent Algorithms for (Relaxed) Minimax Fairness

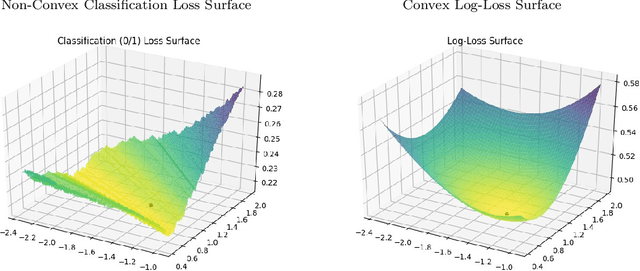
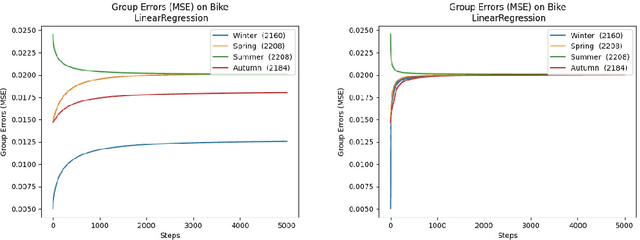
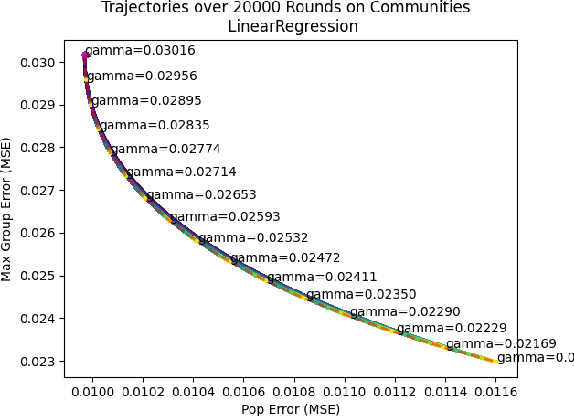
We consider a recently introduced framework in which fairness is measured by worst-case outcomes across groups, rather than by the more standard $\textit{difference}$ between group outcomes. In this framework we provide provably convergent $\textit{oracle-efficient}$ learning algorithms (or equivalently, reductions to non-fair learning) for $\textit{minimax group fairness}$. Here the goal is that of minimizing the maximum loss across all groups, rather than equalizing group losses. Our algorithms apply to both regression and classification settings and support both overall error and false positive or false negative rates as the fairness measure of interest. They also support relaxations of the fairness constraints, thus permitting study of the tradeoff between overall accuracy and minimax fairness. We compare the experimental behavior and performance of our algorithms across a variety of fairness-sensitive data sets and show cases in which minimax fairness is strictly and strongly preferable to equal outcome notions, in the sense that equal outcomes can only be obtained by artificially inflating the harm inflicted on some groups compared to what they suffer under the minimax solution.

Algorithms and Learning for Fair Portfolio Design

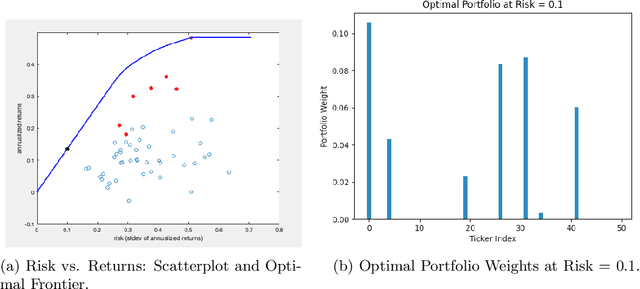
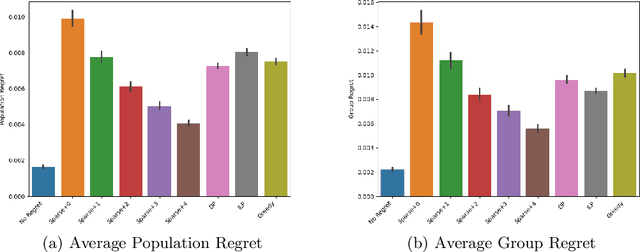
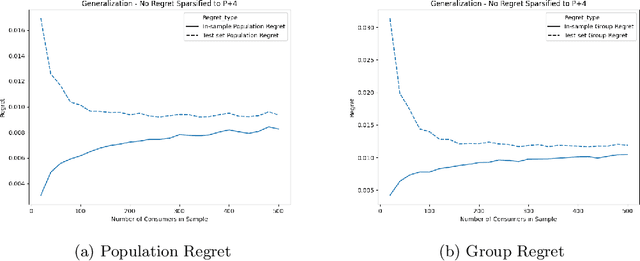
We consider a variation on the classical finance problem of optimal portfolio design. In our setting, a large population of consumers is drawn from some distribution over risk tolerances, and each consumer must be assigned to a portfolio of lower risk than her tolerance. The consumers may also belong to underlying groups (for instance, of demographic properties or wealth), and the goal is to design a small number of portfolios that are fair across groups in a particular and natural technical sense. Our main results are algorithms for optimal and near-optimal portfolio design for both social welfare and fairness objectives, both with and without assumptions on the underlying group structure. We describe an efficient algorithm based on an internal two-player zero-sum game that learns near-optimal fair portfolios ex ante and show experimentally that it can be used to obtain a small set of fair portfolios ex post as well. For the special but natural case in which group structure coincides with risk tolerances (which models the reality that wealthy consumers generally tolerate greater risk), we give an efficient and optimal fair algorithm. We also provide generalization guarantees for the underlying risk distribution that has no dependence on the number of portfolios and illustrate the theory with simulation results.

Optimal, Truthful, and Private Securities Lending

We consider a fundamental dynamic allocation problem motivated by the problem of $\textit{securities lending}$ in financial markets, the mechanism underlying the short selling of stocks. A lender would like to distribute a finite number of identical copies of some scarce resource to $n$ clients, each of whom has a private demand that is unknown to the lender. The lender would like to maximize the usage of the resource $\mbox{---}$ avoiding allocating more to a client than her true demand $\mbox{---}$ but is constrained to sell the resource at a pre-specified price per unit, and thus cannot use prices to incentivize truthful reporting. We first show that the Bayesian optimal algorithm for the one-shot problem $\mbox{---}$ which maximizes the resource's expected usage according to the posterior expectation of demand, given reports $\mbox{---}$ actually incentivizes truthful reporting as a dominant strategy. Because true demands in the securities lending problem are often sensitive information that the client would like to hide from competitors, we then consider the problem under the additional desideratum of (joint) differential privacy. We give an algorithm, based on simple dynamics for computing market equilibria, that is simultaneously private, approximately optimal, and approximately dominant-strategy truthful. Finally, we leverage this private algorithm to construct an approximately truthful, optimal mechanism for the extensive form multi-round auction where the lender does not have access to the true joint distributions between clients' requests and demands.