Estimating and Implementing Conventional Fairness Metrics With Probabilistic Protected Features

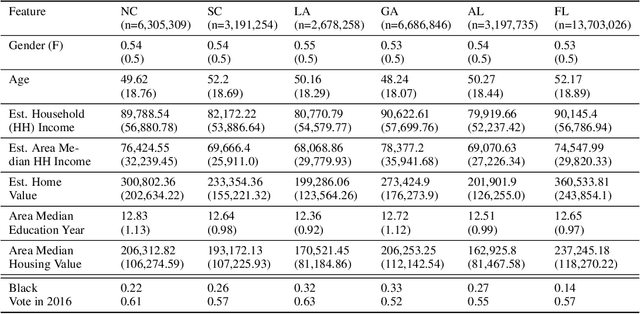
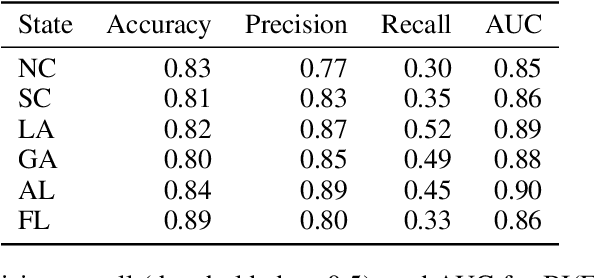
The vast majority of techniques to train fair models require access to the protected attribute (e.g., race, gender), either at train time or in production. However, in many important applications this protected attribute is largely unavailable. In this paper, we develop methods for measuring and reducing fairness violations in a setting with limited access to protected attribute labels. Specifically, we assume access to protected attribute labels on a small subset of the dataset of interest, but only probabilistic estimates of protected attribute labels (e.g., via Bayesian Improved Surname Geocoding) for the rest of the dataset. With this setting in mind, we propose a method to estimate bounds on common fairness metrics for an existing model, as well as a method for training a model to limit fairness violations by solving a constrained non-convex optimization problem. Unlike similar existing approaches, our methods take advantage of contextual information -- specifically, the relationships between a model's predictions and the probabilistic prediction of protected attributes, given the true protected attribute, and vice versa -- to provide tighter bounds on the true disparity. We provide an empirical illustration of our methods using voting data. First, we show our measurement method can bound the true disparity up to 5.5x tighter than previous methods in these applications. Then, we demonstrate that our training technique effectively reduces disparity while incurring lesser fairness-accuracy trade-offs than other fair optimization methods with limited access to protected attributes.

Algorithmic Fairness and Vertical Equity: Income Fairness with IRS Tax Audit Models

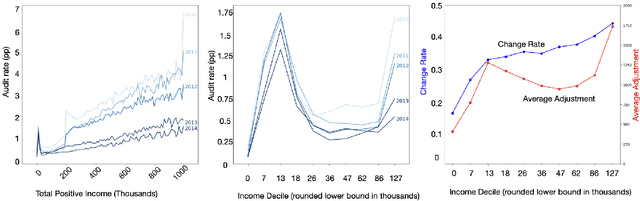
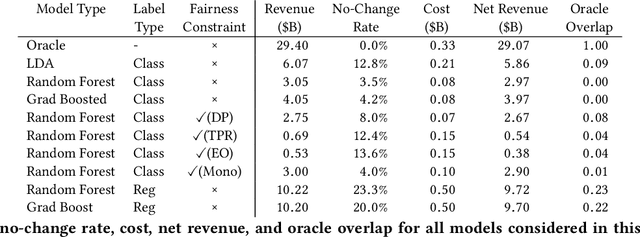
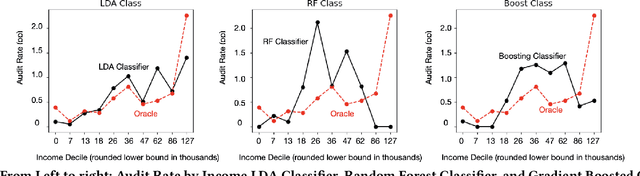
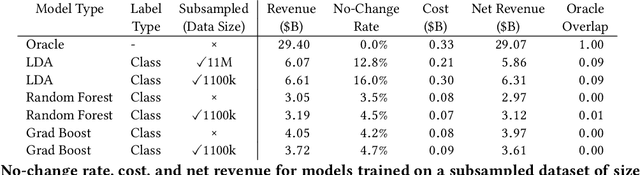
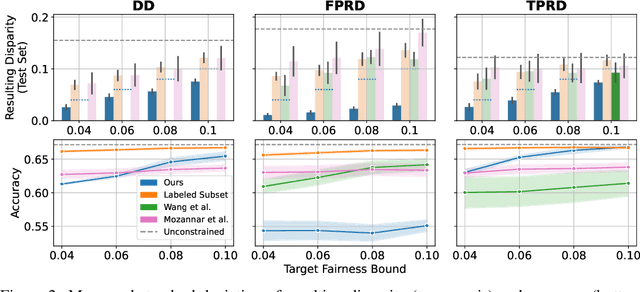
This study examines issues of algorithmic fairness in the context of systems that inform tax audit selection by the United States Internal Revenue Service (IRS). While the field of algorithmic fairness has developed primarily around notions of treating like individuals alike, we instead explore the concept of vertical equity -- appropriately accounting for relevant differences across individuals -- which is a central component of fairness in many public policy settings. Applied to the design of the U.S. individual income tax system, vertical equity relates to the fair allocation of tax and enforcement burdens across taxpayers of different income levels. Through a unique collaboration with the Treasury Department and IRS, we use access to anonymized individual taxpayer microdata, risk-selected audits, and random audits from 2010-14 to study vertical equity in tax administration. In particular, we assess how the use of modern machine learning methods for selecting audits may affect vertical equity. First, we show how the use of more flexible machine learning (classification) methods -- as opposed to simpler models -- shifts audit burdens from high to middle-income taxpayers. Second, we show that while existing algorithmic fairness techniques can mitigate some disparities across income, they can incur a steep cost to performance. Third, we show that the choice of whether to treat risk of underreporting as a classification or regression problem is highly consequential. Moving from classification to regression models to predict underreporting shifts audit burden substantially toward high income individuals, while increasing revenue. Last, we explore the role of differential audit cost in shaping the audit distribution. We show that a narrow focus on return-on-investment can undermine vertical equity. Our results have implications for the design of algorithmic tools across the public sector.

Algorithms and Learning for Fair Portfolio Design

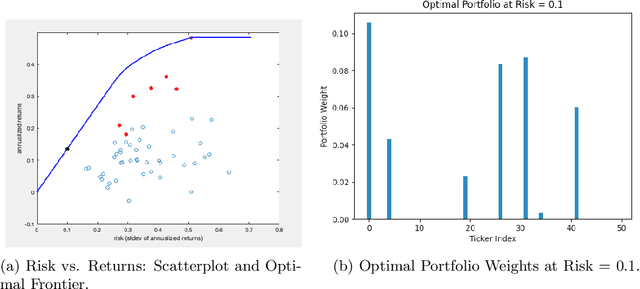
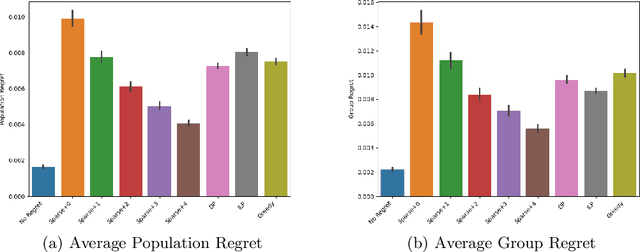
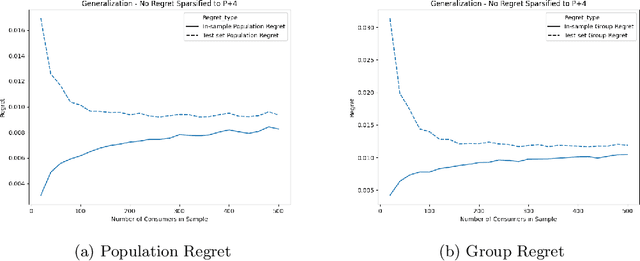
We consider a variation on the classical finance problem of optimal portfolio design. In our setting, a large population of consumers is drawn from some distribution over risk tolerances, and each consumer must be assigned to a portfolio of lower risk than her tolerance. The consumers may also belong to underlying groups (for instance, of demographic properties or wealth), and the goal is to design a small number of portfolios that are fair across groups in a particular and natural technical sense. Our main results are algorithms for optimal and near-optimal portfolio design for both social welfare and fairness objectives, both with and without assumptions on the underlying group structure. We describe an efficient algorithm based on an internal two-player zero-sum game that learns near-optimal fair portfolios ex ante and show experimentally that it can be used to obtain a small set of fair portfolios ex post as well. For the special but natural case in which group structure coincides with risk tolerances (which models the reality that wealthy consumers generally tolerate greater risk), we give an efficient and optimal fair algorithm. We also provide generalization guarantees for the underlying risk distribution that has no dependence on the number of portfolios and illustrate the theory with simulation results.

Equilibrium Characterization for Data Acquisition Games

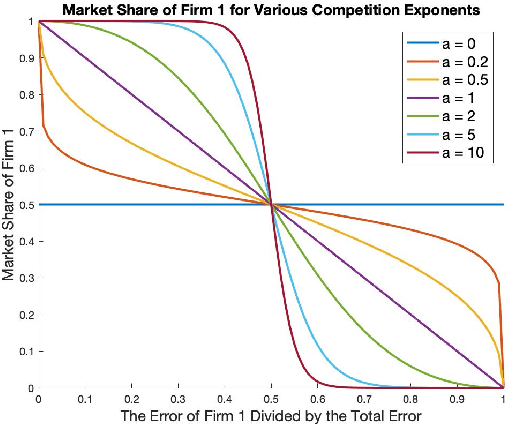
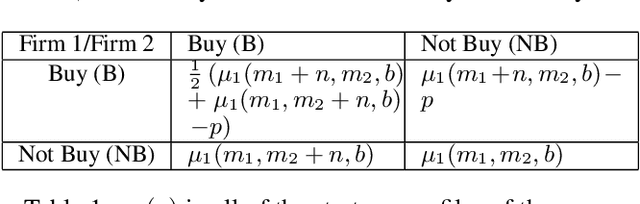
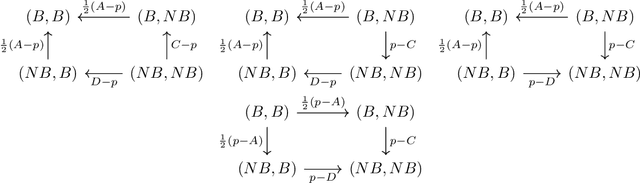
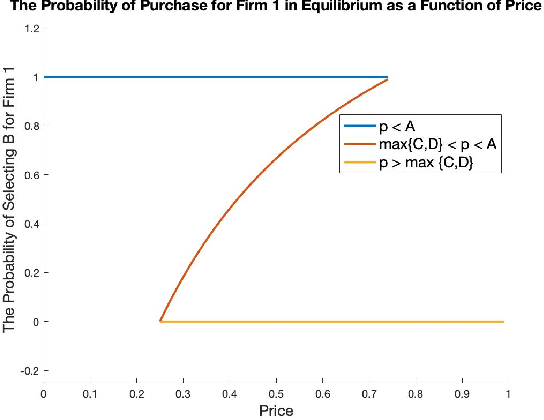
We study a game between two firms in which each provide a service based on machine learning. The firms are presented with the opportunity to purchase a new corpus of data, which will allow them to potentially improve the quality of their products. The firms can decide whether or not they want to buy the data, as well as which learning model to build with that data. We demonstrate a reduction from this potentially complicated action space to a one-shot, two-action game in which each firm only decides whether or not to buy the data. The game admits several regimes which depend on the relative strength of the two firms at the outset and the price at which the data is being offered. We analyze the game's Nash equilibria in all parameter regimes and demonstrate that, in expectation, the outcome of the game is that the initially stronger firm's market position weakens whereas the initially weaker firm's market position becomes stronger. Finally, we consider the perspective of the users of the service and demonstrate that the expected outcome at equilibrium is not the one which maximizes the welfare of the consumers.

Fair Algorithms for Learning in Allocation Problems

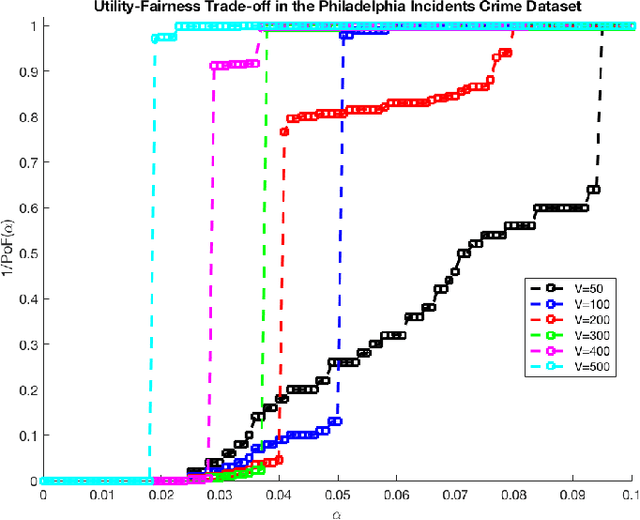
Settings such as lending and policing can be modeled by a centralized agent allocating a resource (loans or police officers) amongst several groups, in order to maximize some objective (loans given that are repaid or criminals that are apprehended). Often in such problems fairness is also a concern. A natural notion of fairness, based on general principles of equality of opportunity, asks that conditional on an individual being a candidate for the resource, the probability of actually receiving it is approximately independent of the individual's group. In lending this means that equally creditworthy individuals in different racial groups have roughly equal chances of receiving a loan. In policing it means that two individuals committing the same crime in different districts would have roughly equal chances of being arrested. We formalize this fairness notion for allocation problems and investigate its algorithmic consequences. Our main technical results include an efficient learning algorithm that converges to an optimal fair allocation even when the frequency of candidates (creditworthy individuals or criminals) in each group is unknown. The algorithm operates in a censored feedback model in which only the number of candidates who received the resource in a given allocation can be observed, rather than the true number of candidates. This models the fact that we do not learn the creditworthiness of individuals we do not give loans to nor learn about crimes committed if the police presence in a district is low. As an application of our framework, we consider the predictive policing problem. The learning algorithm is trained on arrest data gathered from its own deployments on previous days, resulting in a potential feedback loop that our algorithm provably overcomes. We empirically investigate the performance of our algorithm on the Philadelphia Crime Incidents dataset.