Error-Tolerant E-Discovery Protocols

We consider the multi-party classification problem introduced by Dong, Hartline, and Vijayaraghavan (2022) in the context of electronic discovery (e-discovery). Based on a request for production from the requesting party, the responding party is required to provide documents that are responsive to the request except for those that are legally privileged. Our goal is to find a protocol that verifies that the responding party sends almost all responsive documents while minimizing the disclosure of non-responsive documents. We provide protocols in the challenging non-realizable setting, where the instance may not be perfectly separated by a linear classifier. We demonstrate empirically that our protocol successfully manages to find almost all relevant documents, while incurring only a small disclosure of non-responsive documents. We complement this with a theoretical analysis of our protocol in the single-dimensional setting, and other experiments on simulated data which suggest that the non-responsive disclosure incurred by our protocol may be unavoidable.

Classification Protocols with Minimal Disclosure

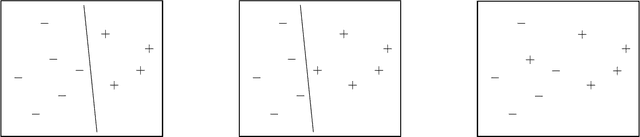
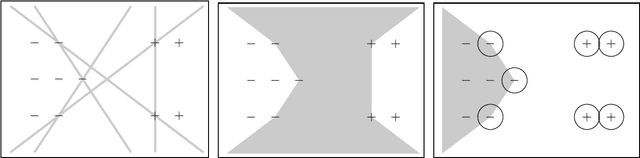
We consider multi-party protocols for classification that are motivated by applications such as e-discovery in court proceedings. We identify a protocol that guarantees that the requesting party receives all responsive documents and the sending party discloses the minimal amount of non-responsive documents necessary to prove that all responsive documents have been received. This protocol can be embedded in a machine learning framework that enables automated labeling of points and the resulting multi-party protocol is equivalent to the standard one-party classification problem (if the one-party classification problem satisfies a natural independence-of-irrelevant-alternatives property). Our formal guarantees focus on the case where there is a linear classifier that correctly partitions the documents.

Privacy Amplification via Iteration for Shuffled and Online PNSGD

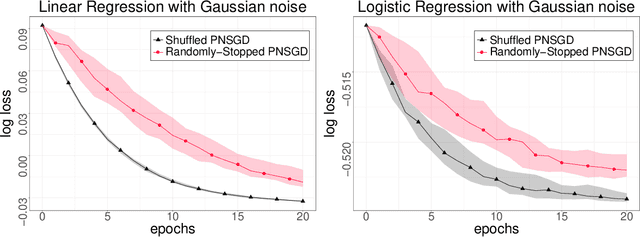
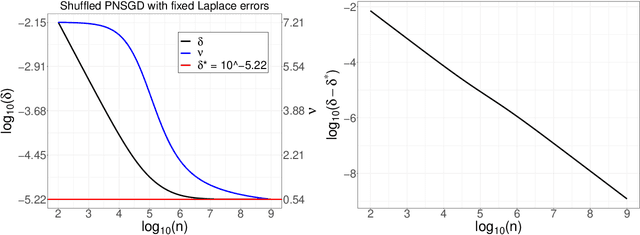
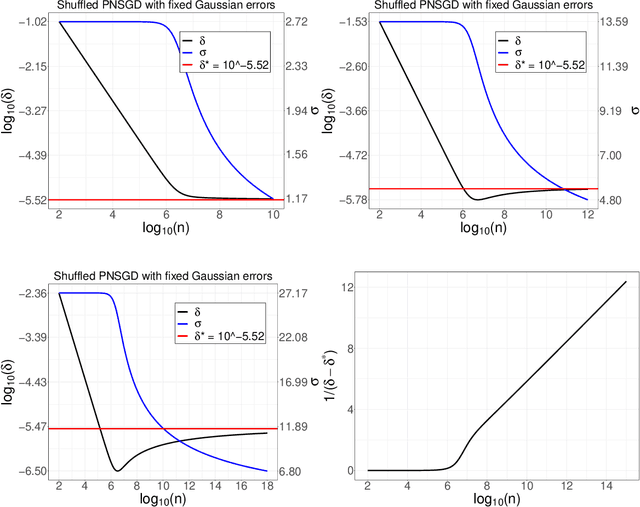
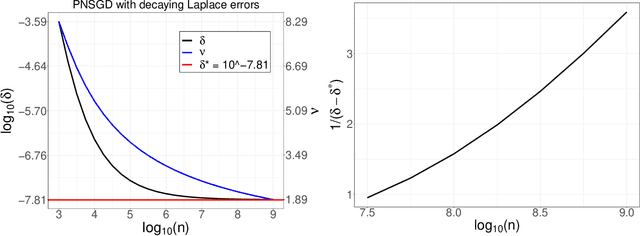
In this paper, we consider the framework of privacy amplification via iteration, which is originally proposed by Feldman et al. and subsequently simplified by Asoodeh et al. in their analysis via the contraction coefficient. This line of work focuses on the study of the privacy guarantees obtained by the projected noisy stochastic gradient descent (PNSGD) algorithm with hidden intermediate updates. A limitation in the existing literature is that only the early stopped PNSGD has been studied, while no result has been proved on the more widely-used PNSGD applied on a shuffled dataset. Moreover, no scheme has been yet proposed regarding how to decrease the injected noise when new data are received in an online fashion. In this work, we first prove a privacy guarantee for shuffled PNSGD, which is investigated asymptotically when the noise is fixed for each sample size $n$ but reduced at a predetermined rate when $n$ increases, in order to achieve the convergence of privacy loss. We then analyze the online setting and provide a faster decaying scheme for the magnitude of the injected noise that also guarantees the convergence of privacy loss.

Optimal Accounting of Differential Privacy via Characteristic Function

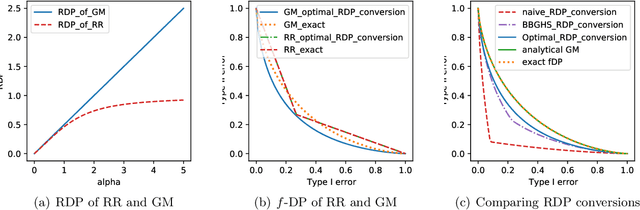
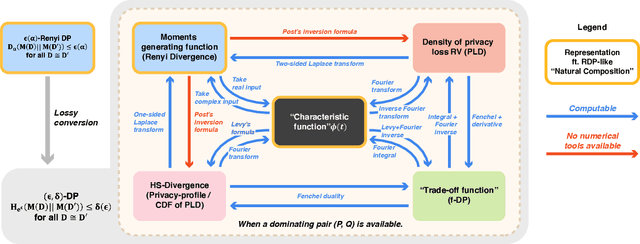
Characterizing the privacy degradation over compositions, i.e., privacy accounting, is a fundamental topic in differential privacy (DP) with many applications to differentially private machine learning and federated learning. We propose a unification of recent advances (Renyi DP, privacy profiles, $f$-DP and the PLD formalism) via the characteristic function ($\phi$-function) of a certain ``worst-case'' privacy loss random variable. We show that our approach allows natural adaptive composition like Renyi DP, provides exactly tight privacy accounting like PLD, and can be (often losslessly) converted to privacy profile and $f$-DP, thus providing $(\epsilon,\delta)$-DP guarantees and interpretable tradeoff functions. Algorithmically, we propose an analytical Fourier accountant that represents the complex logarithm of $\phi$-functions symbolically and uses Gaussian quadrature for numerical computation. On several popular DP mechanisms and their subsampled counterparts, we demonstrate the flexibility and tightness of our approach in theory and experiments.

Rejoinder: Gaussian Differential Privacy

In this rejoinder, we aim to address two broad issues that cover most comments made in the discussion. First, we discuss some theoretical aspects of our work and comment on how this work might impact the theoretical foundation of privacy-preserving data analysis. Taking a practical viewpoint, we next discuss how f-differential privacy (f-DP) and Gaussian differential privacy (GDP) can make a difference in a range of applications.

A Central Limit Theorem for Differentially Private Query Answering

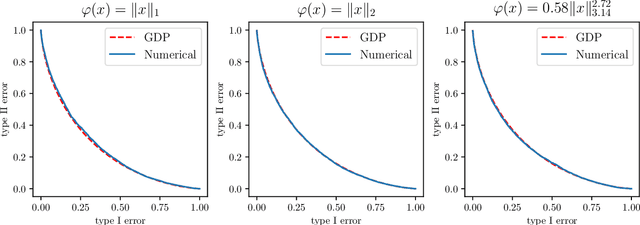
Perhaps the single most important use case for differential privacy is to privately answer numerical queries, which is usually achieved by adding noise to the answer vector. The central question, therefore, is to understand which noise distribution optimizes the privacy-accuracy trade-off, especially when the dimension of the answer vector is high. Accordingly, extensive literature has been dedicated to the question and the upper and lower bounds have been matched up to constant factors [BUV18, SU17]. In this paper, we take a novel approach to address this important optimality question. We first demonstrate an intriguing central limit theorem phenomenon in the high-dimensional regime. More precisely, we prove that a mechanism is approximately Gaussian Differentially Private [DRS21] if the added noise satisfies certain conditions. In particular, densities proportional to $\mathrm{e}^{-\|x\|_p^\alpha}$, where $\|x\|_p$ is the standard $\ell_p$-norm, satisfies the conditions. Taking this perspective, we make use of the Cramer--Rao inequality and show an "uncertainty principle"-style result: the product of the privacy parameter and the $\ell_2$-loss of the mechanism is lower bounded by the dimension. Furthermore, the Gaussian mechanism achieves the constant-sharp optimal privacy-accuracy trade-off among all such noises. Our findings are corroborated by numerical experiments.

Sharp Composition Bounds for Gaussian Differential Privacy via Edgeworth Expansion

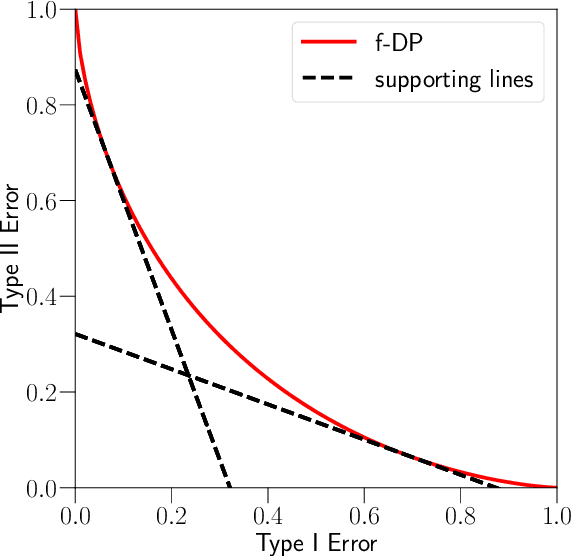
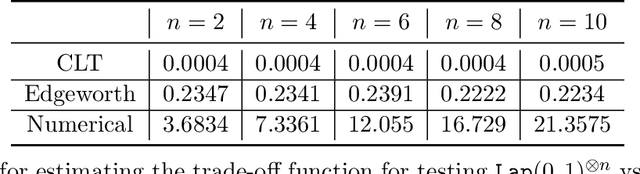
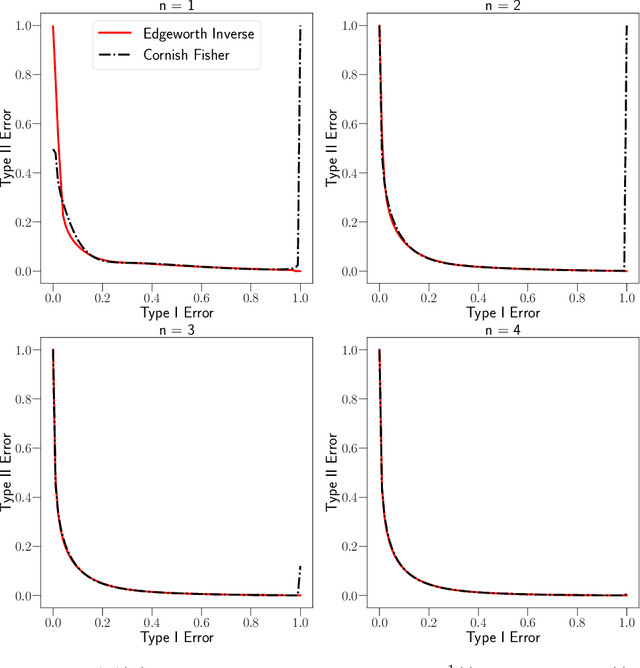
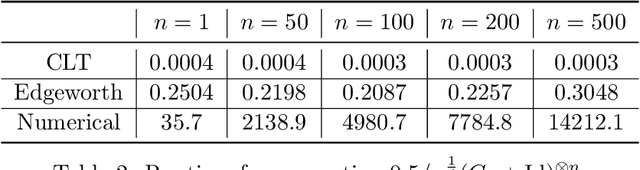
Datasets containing sensitive information are often sequentially analyzed by many algorithms. This raises a fundamental question in differential privacy regarding how the overall privacy bound degrades under composition. To address this question, we introduce a family of analytical and sharp privacy bounds under composition using the Edgeworth expansion in the framework of the recently proposed f-differential privacy. In contrast to the existing composition theorems using the central limit theorem, our new privacy bounds under composition gain improved tightness by leveraging the refined approximation accuracy of the Edgeworth expansion. Our approach is easy to implement and computationally efficient for any number of compositions. The superiority of these new bounds is confirmed by an asymptotic error analysis and an application to quantifying the overall privacy guarantees of noisy stochastic gradient descent used in training private deep neural networks.

Deep Learning with Gaussian Differential Privacy

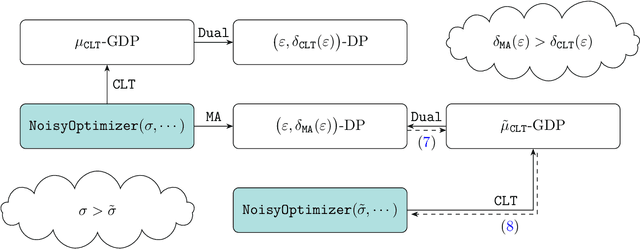
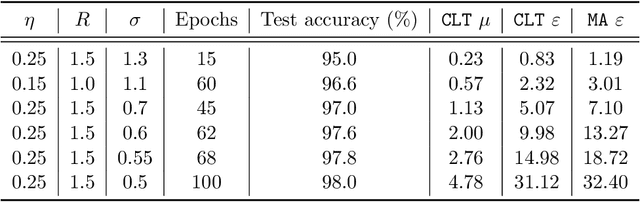
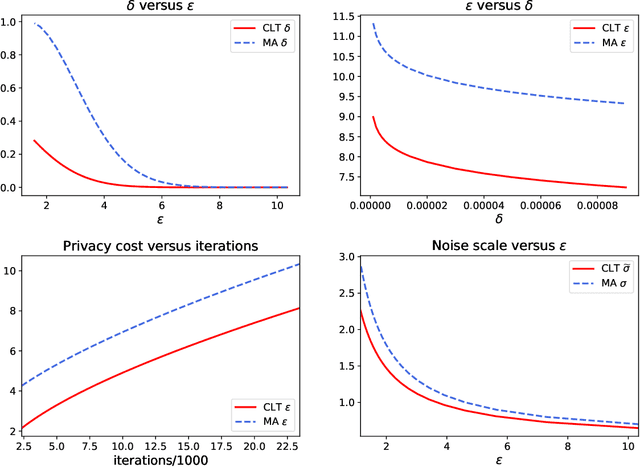
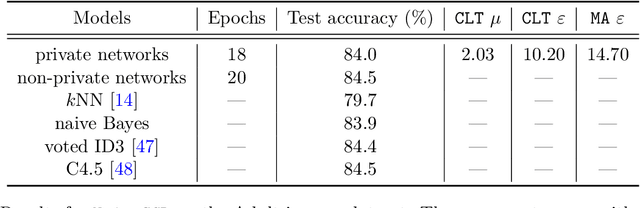
Deep learning models are often trained on datasets that contain sensitive information such as individuals' shopping transactions, personal contacts, and medical records. An increasingly important line of work therefore has sought to train neural networks subject to privacy constraints that are specified by differential privacy or its divergence-based relaxations. These privacy definitions, however, have weaknesses in handling certain important primitives (composition and subsampling), thereby giving loose or complicated privacy analyses of training neural networks. In this paper, we consider a recently proposed privacy definition termed f-differential privacy [17] for a refined privacy analysis of training neural networks. Leveraging the appealing properties of f-differential privacy in handling composition and subsampling, this paper derives analytically tractable expressions for the privacy guarantees of both stochastic gradient descent and Adam used in training deep neural networks, without the need of developing sophisticated techniques as [3] did. Our results demonstrate that the f-differential privacy framework allows for a new privacy analysis that improves on the prior analysis [3], which in turn suggests tuning certain parameters of neural networks for a better prediction accuracy without violating the privacy budget. These theoretically derived improvements are confirmed by our experiments in a range of tasks in image classification, text classification, and recommender systems.

Gaussian Differential Privacy

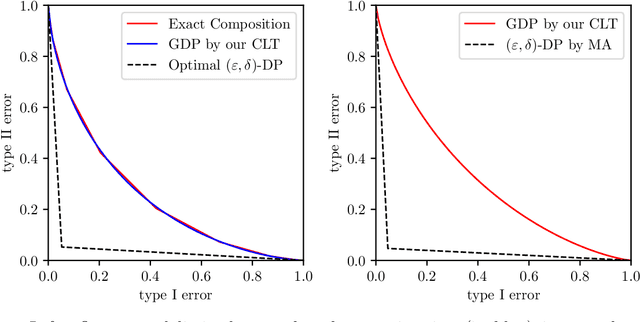
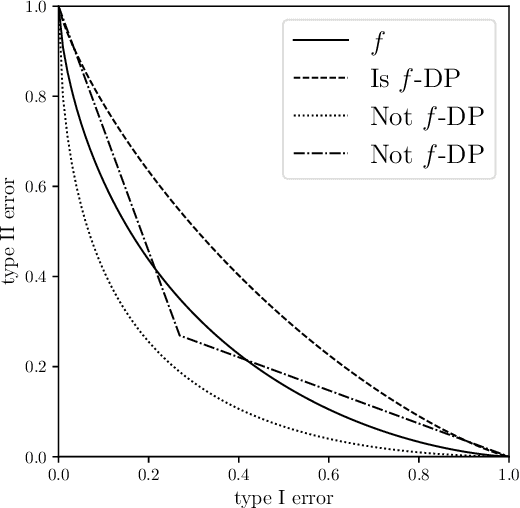
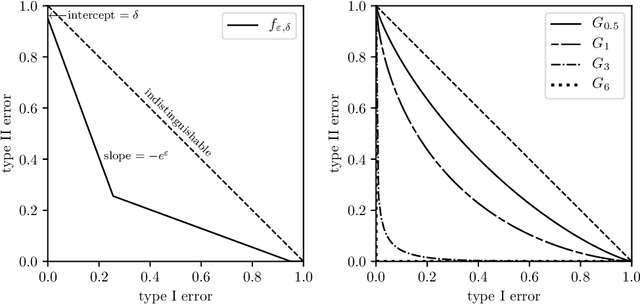
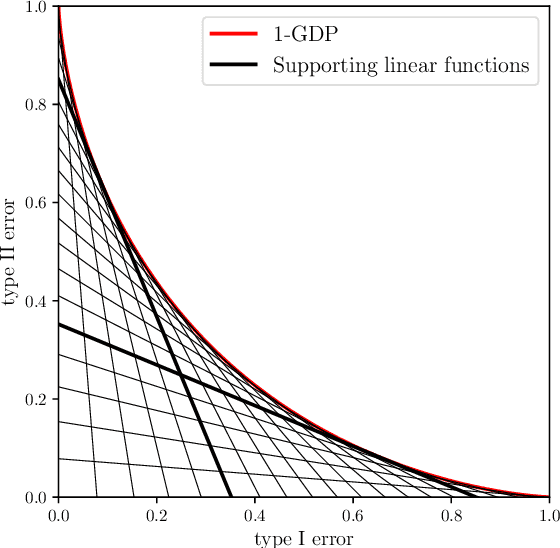
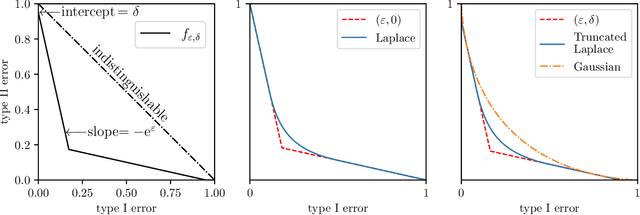
Differential privacy has seen remarkable success as a rigorous and practical formalization of data privacy in the past decade. This privacy definition and its divergence based relaxations, however, have several acknowledged weaknesses, either in handling composition of private algorithms or in analyzing important primitives like privacy amplification by subsampling. Inspired by the hypothesis testing formulation of privacy, this paper proposes a new relaxation, which we term `$f$-differential privacy' ($f$-DP). This notion of privacy has a number of appealing properties and, in particular, avoids difficulties associated with divergence based relaxations. First, $f$-DP preserves the hypothesis testing interpretation. In addition, $f$-DP allows for lossless reasoning about composition in an algebraic fashion. Moreover, we provide a powerful technique to import existing results proven for original DP to $f$-DP and, as an application, obtain a simple subsampling theorem for $f$-DP. In addition to the above findings, we introduce a canonical single-parameter family of privacy notions within the $f$-DP class that is referred to as `Gaussian differential privacy' (GDP), defined based on testing two shifted Gaussians. GDP is focal among the $f$-DP class because of a central limit theorem we prove. More precisely, the privacy guarantees of \emph{any} hypothesis testing based definition of privacy (including original DP) converges to GDP in the limit under composition. The CLT also yields a computationally inexpensive tool for analyzing the exact composition of private algorithms. Taken together, this collection of attractive properties render $f$-DP a mathematically coherent, analytically tractable, and versatile framework for private data analysis. Finally, we demonstrate the use of the tools we develop by giving an improved privacy analysis of noisy stochastic gradient descent.

Equilibrium Characterization for Data Acquisition Games

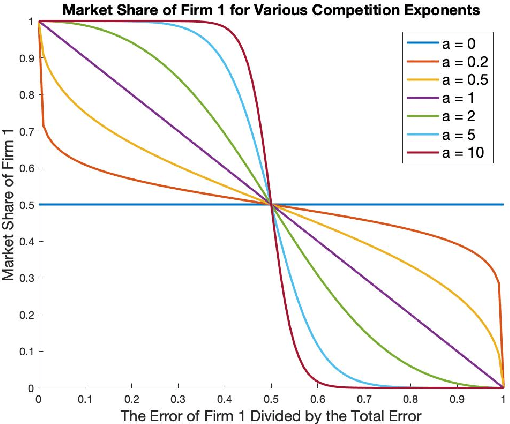
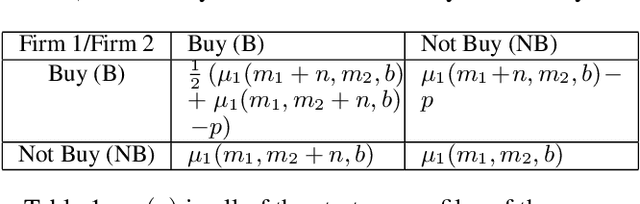
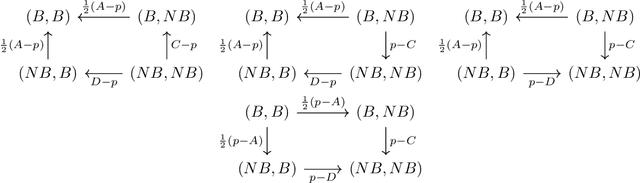
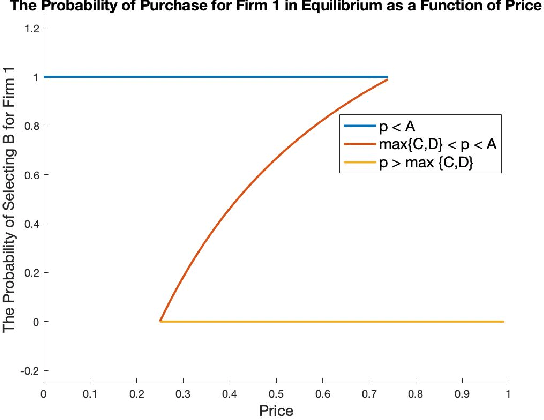
We study a game between two firms in which each provide a service based on machine learning. The firms are presented with the opportunity to purchase a new corpus of data, which will allow them to potentially improve the quality of their products. The firms can decide whether or not they want to buy the data, as well as which learning model to build with that data. We demonstrate a reduction from this potentially complicated action space to a one-shot, two-action game in which each firm only decides whether or not to buy the data. The game admits several regimes which depend on the relative strength of the two firms at the outset and the price at which the data is being offered. We analyze the game's Nash equilibria in all parameter regimes and demonstrate that, in expectation, the outcome of the game is that the initially stronger firm's market position weakens whereas the initially weaker firm's market position becomes stronger. Finally, we consider the perspective of the users of the service and demonstrate that the expected outcome at equilibrium is not the one which maximizes the welfare of the consumers.