Aravindan Vijayaraghavan
Learning Confidence Ellipsoids and Applications to Robust Subspace Recovery
Dec 19, 2025

Abstract:We study the problem of finding confidence ellipsoids for an arbitrary distribution in high dimensions. Given samples from a distribution $D$ and a confidence parameter $α$, the goal is to find the smallest volume ellipsoid $E$ which has probability mass $\Pr_{D}[E] \ge 1-α$. Ellipsoids are a highly expressive class of confidence sets as they can capture correlations in the distribution, and can approximate any convex set. This problem has been studied in many different communities. In statistics, this is the classic minimum volume estimator introduced by Rousseeuw as a robust non-parametric estimator of location and scatter. However in high dimensions, it becomes NP-hard to obtain any non-trivial approximation factor in volume when the condition number $β$ of the ellipsoid (ratio of the largest to the smallest axis length) goes to $\infty$. This motivates the focus of our paper: can we efficiently find confidence ellipsoids with volume approximation guarantees when compared to ellipsoids of bounded condition number $β$? Our main result is a polynomial time algorithm that finds an ellipsoid $E$ whose volume is within a $O(β)^{γd}$ multiplicative factor of the volume of best $β$-conditioned ellipsoid while covering at least $1-O(α/γ)$ probability mass for any $γ< α$. We complement this with a computational hardness result that shows that such a dependence seems necessary up to constants in the exponent. The algorithm and analysis uses the rich primal-dual structure of the minimum volume enclosing ellipsoid and the geometric Brascamp-Lieb inequality. As a consequence, we obtain the first polynomial time algorithm with approximation guarantees on worst-case instances of the robust subspace recovery problem.
Computing High-dimensional Confidence Sets for Arbitrary Distributions
Apr 03, 2025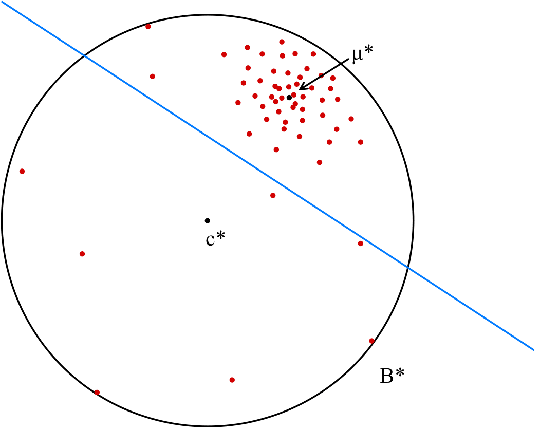
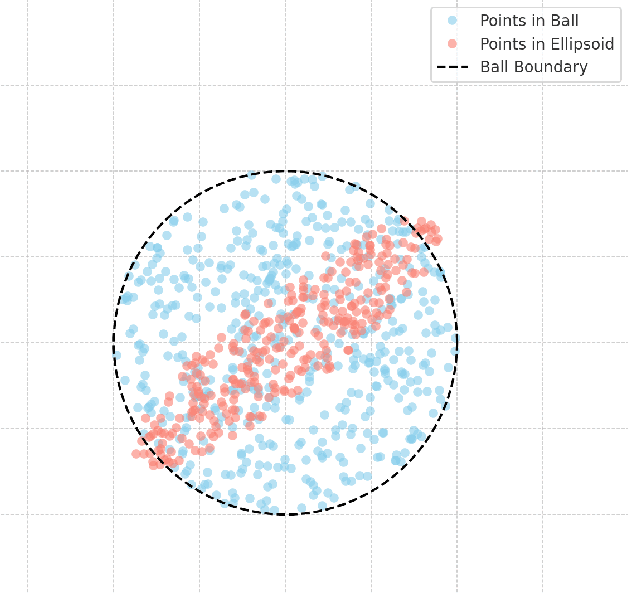


Abstract:We study the problem of learning a high-density region of an arbitrary distribution over $\mathbb{R}^d$. Given a target coverage parameter $\delta$, and sample access to an arbitrary distribution $D$, we want to output a confidence set $S \subset \mathbb{R}^d$ such that $S$ achieves $\delta$ coverage of $D$, i.e., $\mathbb{P}_{y \sim D} \left[ y \in S \right] \ge \delta$, and the volume of $S$ is as small as possible. This is a central problem in high-dimensional statistics with applications in finding confidence sets, uncertainty quantification, and support estimation. In the most general setting, this problem is statistically intractable, so we restrict our attention to competing with sets from a concept class $C$ with bounded VC-dimension. An algorithm is competitive with class $C$ if, given samples from an arbitrary distribution $D$, it outputs in polynomial time a set that achieves $\delta$ coverage of $D$, and whose volume is competitive with the smallest set in $C$ with the required coverage $\delta$. This problem is computationally challenging even in the basic setting when $C$ is the set of all Euclidean balls. Existing algorithms based on coresets find in polynomial time a ball whose volume is $\exp(\tilde{O}( d/ \log d))$-factor competitive with the volume of the best ball. Our main result is an algorithm that finds a confidence set whose volume is $\exp(\tilde{O}(d^{2/3}))$ factor competitive with the optimal ball having the desired coverage. The algorithm is improper (it outputs an ellipsoid). Combined with our computational intractability result for proper learning balls within an $\exp(\tilde{O}(d^{1-o(1)}))$ approximation factor in volume, our results provide an interesting separation between proper and (improper) learning of confidence sets.
Volume Optimality in Conformal Prediction with Structured Prediction Sets
Feb 23, 2025Abstract:Conformal Prediction is a widely studied technique to construct prediction sets of future observations. Most conformal prediction methods focus on achieving the necessary coverage guarantees, but do not provide formal guarantees on the size (volume) of the prediction sets. We first prove an impossibility of volume optimality where any distribution-free method can only find a trivial solution. We then introduce a new notion of volume optimality by restricting the prediction sets to belong to a set family (of finite VC-dimension), specifically a union of $k$-intervals. Our main contribution is an efficient distribution-free algorithm based on dynamic programming (DP) to find a union of $k$-intervals that is guaranteed for any distribution to have near-optimal volume among all unions of $k$-intervals satisfying the desired coverage property. By adopting the framework of distributional conformal prediction (Chernozhukov et al., 2021), the new DP based conformity score can also be applied to achieve approximate conditional coverage and conditional restricted volume optimality, as long as a reasonable estimator of the conditional CDF is available. While the theoretical results already establish volume-optimality guarantees, they are complemented by experiments that demonstrate that our method can significantly outperform existing methods in many settings.
Agnostic Learning of Arbitrary ReLU Activation under Gaussian Marginals
Nov 22, 2024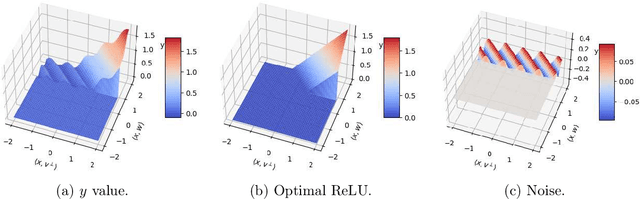
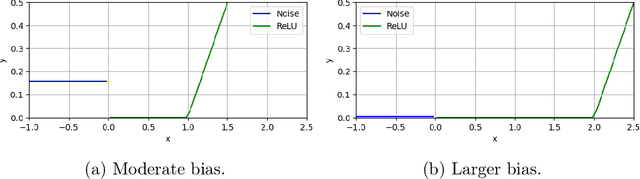
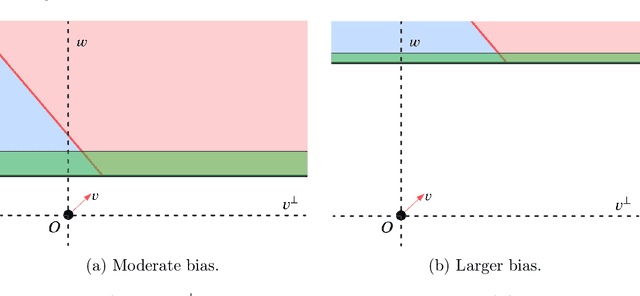
Abstract:We consider the problem of learning an arbitrarily-biased ReLU activation (or neuron) over Gaussian marginals with the squared loss objective. Despite the ReLU neuron being the basic building block of modern neural networks, we still do not understand the basic algorithmic question of whether one arbitrary ReLU neuron is learnable in the non-realizable setting. In particular, all existing polynomial time algorithms only provide approximation guarantees for the better-behaved unbiased setting or restricted bias setting. Our main result is a polynomial time statistical query (SQ) algorithm that gives the first constant factor approximation for arbitrary bias. It outputs a ReLU activation that achieves a loss of $O(\mathrm{OPT}) + \varepsilon$ in time $\mathrm{poly}(d,1/\varepsilon)$, where $\mathrm{OPT}$ is the loss obtained by the optimal ReLU activation. Our algorithm presents an interesting departure from existing algorithms, which are all based on gradient descent and thus fall within the class of correlational statistical query (CSQ) algorithms. We complement our algorithmic result by showing that no polynomial time CSQ algorithm can achieve a constant factor approximation. Together, these results shed light on the intrinsic limitation of gradient descent, while identifying arguably the simplest setting (a single neuron) where there is a separation between SQ and CSQ algorithms.
Theoretical Analysis of Weak-to-Strong Generalization
May 25, 2024Abstract:Strong student models can learn from weaker teachers: when trained on the predictions of a weaker model, a strong pretrained student can learn to correct the weak model's errors and generalize to examples where the teacher is not confident, even when these examples are excluded from training. This enables learning from cheap, incomplete, and possibly incorrect label information, such as coarse logical rules or the generations of a language model. We show that existing weak supervision theory fails to account for both of these effects, which we call pseudolabel correction and coverage expansion, respectively. We give a new bound based on expansion properties of the data distribution and student hypothesis class that directly accounts for pseudolabel correction and coverage expansion. Our bounds capture the intuition that weak-to-strong generalization occurs when the strong model is unable to fit the mistakes of the weak teacher without incurring additional error. We show that these expansion properties can be checked from finite data and give empirical evidence that they hold in practice.
Efficient Certificates of Anti-Concentration Beyond Gaussians
May 23, 2024Abstract:A set of high dimensional points $X=\{x_1, x_2,\ldots, x_n\} \subset R^d$ in isotropic position is said to be $\delta$-anti concentrated if for every direction $v$, the fraction of points in $X$ satisfying $|\langle x_i,v \rangle |\leq \delta$ is at most $O(\delta)$. Motivated by applications to list-decodable learning and clustering, recent works have considered the problem of constructing efficient certificates of anti-concentration in the average case, when the set of points $X$ corresponds to samples from a Gaussian distribution. Their certificates played a crucial role in several subsequent works in algorithmic robust statistics on list-decodable learning and settling the robust learnability of arbitrary Gaussian mixtures, yet remain limited to rotationally invariant distributions. This work presents a new (and arguably the most natural) formulation for anti-concentration. Using this formulation, we give quasi-polynomial time verifiable sum-of-squares certificates of anti-concentration that hold for a wide class of non-Gaussian distributions including anti-concentrated bounded product distributions and uniform distributions over $L_p$ balls (and their affine transformations). Consequently, our method upgrades and extends results in algorithmic robust statistics e.g., list-decodable learning and clustering, to such distributions. Our approach constructs a canonical integer program for anti-concentration and analysis a sum-of-squares relaxation of it, independent of the intended application. We rely on duality and analyze a pseudo-expectation on large subsets of the input points that take a small value in some direction. Our analysis uses the method of polynomial reweightings to reduce the problem to analyzing only analytically dense or sparse directions.
Error-Tolerant E-Discovery Protocols
Jan 31, 2024Abstract:We consider the multi-party classification problem introduced by Dong, Hartline, and Vijayaraghavan (2022) in the context of electronic discovery (e-discovery). Based on a request for production from the requesting party, the responding party is required to provide documents that are responsive to the request except for those that are legally privileged. Our goal is to find a protocol that verifies that the responding party sends almost all responsive documents while minimizing the disclosure of non-responsive documents. We provide protocols in the challenging non-realizable setting, where the instance may not be perfectly separated by a linear classifier. We demonstrate empirically that our protocol successfully manages to find almost all relevant documents, while incurring only a small disclosure of non-responsive documents. We complement this with a theoretical analysis of our protocol in the single-dimensional setting, and other experiments on simulated data which suggest that the non-responsive disclosure incurred by our protocol may be unavoidable.
Computing linear sections of varieties: quantum entanglement, tensor decompositions and beyond
Dec 07, 2022Abstract:We study the problem of finding elements in the intersection of an arbitrary conic variety in $\mathbb{F}^n$ with a given linear subspace (where $\mathbb{F}$ can be the real or complex field). This problem captures a rich family of algorithmic problems under different choices of the variety. The special case of the variety consisting of rank-1 matrices already has strong connections to central problems in different areas like quantum information theory and tensor decompositions. This problem is known to be NP-hard in the worst-case, even for the variety of rank-1 matrices. Surprisingly, despite these hardness results we give efficient algorithms that solve this problem for "typical" subspaces. Here, the subspace $U \subseteq \mathbb{F}^n$ is chosen generically of a certain dimension, potentially with some generic elements of the variety contained in it. Our main algorithmic result is a polynomial time algorithm that recovers all the elements of $U$ that lie in the variety, under some mild non-degeneracy assumptions on the variety. As corollaries, we obtain the following results: $\bullet$ Uniqueness results and polynomial time algorithms for generic instances of a broad class of low-rank decomposition problems that go beyond tensor decompositions. Here, we recover a decomposition of the form $\sum_{i=1}^R v_i \otimes w_i$, where the $v_i$ are elements of the given variety $X$. This implies new algorithmic results even in the special case of tensor decompositions. $\bullet$ Polynomial time algorithms for several entangled subspaces problems in quantum entanglement, including determining $r$-entanglement, complete entanglement, and genuine entanglement of a subspace. While all of these problems are NP-hard in the worst case, our algorithm solves them in polynomial time for generic subspaces of dimension up to a constant multiple of the maximum possible.
Classification Protocols with Minimal Disclosure
Sep 06, 2022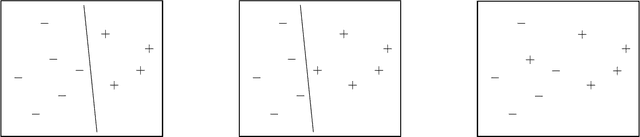
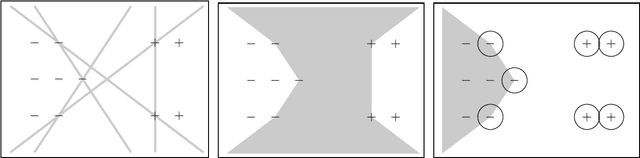
Abstract:We consider multi-party protocols for classification that are motivated by applications such as e-discovery in court proceedings. We identify a protocol that guarantees that the requesting party receives all responsive documents and the sending party discloses the minimal amount of non-responsive documents necessary to prove that all responsive documents have been received. This protocol can be embedded in a machine learning framework that enables automated labeling of points and the resulting multi-party protocol is equivalent to the standard one-party classification problem (if the one-party classification problem satisfies a natural independence-of-irrelevant-alternatives property). Our formal guarantees focus on the case where there is a linear classifier that correctly partitions the documents.
Agnostic Learning of General ReLU Activation Using Gradient Descent
Aug 04, 2022Abstract:We provide a convergence analysis of gradient descent for the problem of agnostically learning a single ReLU function under Gaussian distributions. Unlike prior work that studies the setting of zero bias, we consider the more challenging scenario when the bias of the ReLU function is non-zero. Our main result establishes that starting from random initialization, in a polynomial number of iterations gradient descent outputs, with high probability, a ReLU function that achieves a competitive error guarantee when compared to the error of the best ReLU function. We also provide finite sample guarantees, and these techniques generalize to a broader class of marginal distributions beyond Gaussians.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge