Efficient Certificates of Anti-Concentration Beyond Gaussians

A set of high dimensional points $X=\{x_1, x_2,\ldots, x_n\} \subset R^d$ in isotropic position is said to be $\delta$-anti concentrated if for every direction $v$, the fraction of points in $X$ satisfying $|\langle x_i,v \rangle |\leq \delta$ is at most $O(\delta)$. Motivated by applications to list-decodable learning and clustering, recent works have considered the problem of constructing efficient certificates of anti-concentration in the average case, when the set of points $X$ corresponds to samples from a Gaussian distribution. Their certificates played a crucial role in several subsequent works in algorithmic robust statistics on list-decodable learning and settling the robust learnability of arbitrary Gaussian mixtures, yet remain limited to rotationally invariant distributions. This work presents a new (and arguably the most natural) formulation for anti-concentration. Using this formulation, we give quasi-polynomial time verifiable sum-of-squares certificates of anti-concentration that hold for a wide class of non-Gaussian distributions including anti-concentrated bounded product distributions and uniform distributions over $L_p$ balls (and their affine transformations). Consequently, our method upgrades and extends results in algorithmic robust statistics e.g., list-decodable learning and clustering, to such distributions. Our approach constructs a canonical integer program for anti-concentration and analysis a sum-of-squares relaxation of it, independent of the intended application. We rely on duality and analyze a pseudo-expectation on large subsets of the input points that take a small value in some direction. Our analysis uses the method of polynomial reweightings to reduce the problem to analyzing only analytically dense or sparse directions.

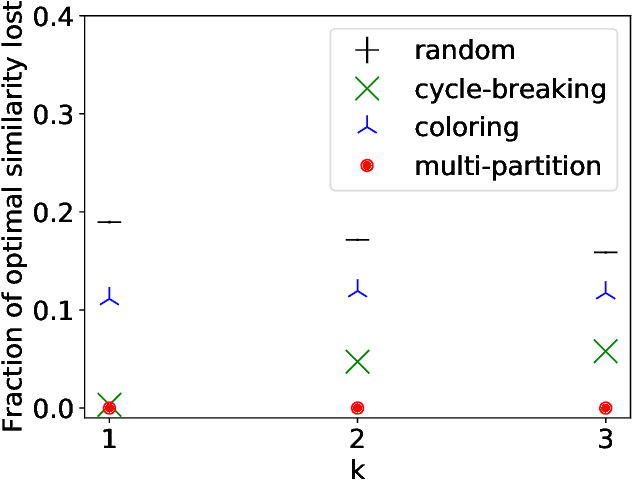
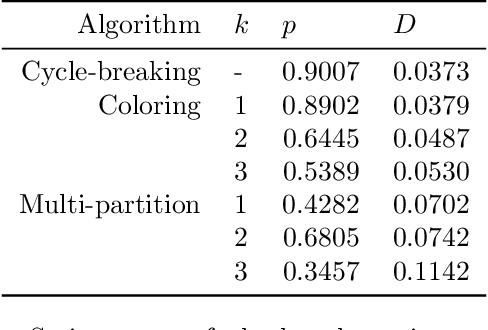
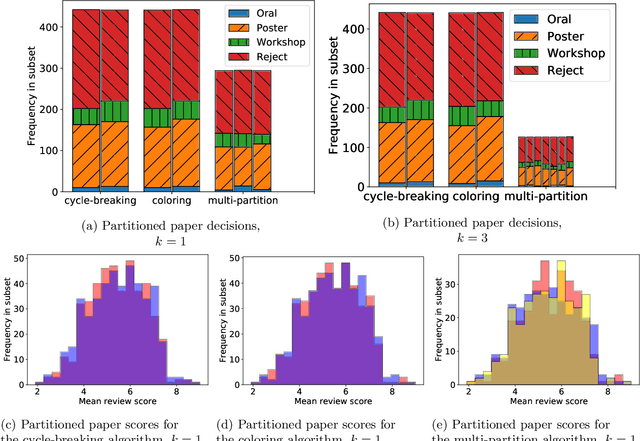
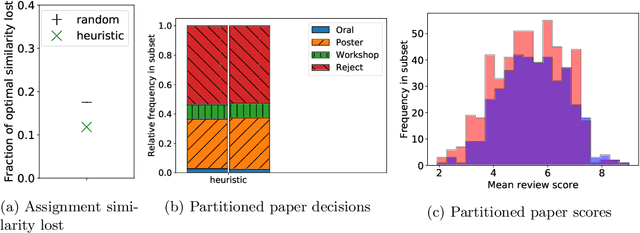
The Price of Strategyproofing Peer Assessment

Strategic behavior is a fundamental problem in a variety of real-world applications that require some form of peer assessment, such as peer grading of assignments, grant proposal review, conference peer review, and peer assessment of employees. Since an individual's own work is in competition with the submissions they are evaluating, they may provide dishonest evaluations to increase the relative standing of their own submission. This issue is typically addressed by partitioning the individuals and assigning them to evaluate the work of only those from different subsets. Although this method ensures strategyproofness, each submission may require a different type of expertise for effective evaluation. In this paper, we focus on finding an assignment of evaluators to submissions that maximizes assigned expertise subject to the constraint of strategyproofness. We analyze the price of strategyproofness: that is, the amount of compromise on the assignment quality required in order to get strategyproofness. We establish several polynomial-time algorithms for strategyproof assignment along with assignment-quality guarantees. Finally, we evaluate the methods on a dataset from conference peer review.

Outlier-Robust Clustering of Non-Spherical Mixtures

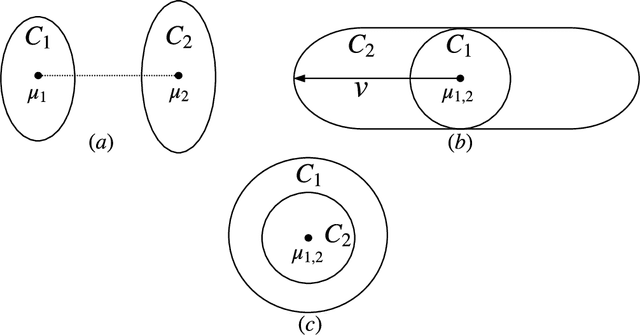
We give the first outlier-robust efficient algorithm for clustering a mixture of $k$ statistically separated d-dimensional Gaussians (k-GMMs). Concretely, our algorithm takes input an $\epsilon$-corrupted sample from a $k$-GMM and whp in $d^{\text{poly}(k/\eta)}$ time, outputs an approximate clustering that misclassifies at most $k^{O(k)}(\epsilon+\eta)$ fraction of the points whenever every pair of mixture components are separated by $1-\exp(-\text{poly}(k/\eta)^k)$ in total variation (TV) distance. Such a result was not previously known even for $k=2$. TV separation is the statistically weakest possible notion of separation and captures important special cases such as mixed linear regression and subspace clustering. Our main conceptual contribution is to distill two simple analytic properties - (certifiable) hypercontractivity and anti-concentration - that are necessary and sufficient for mixture models to be (efficiently) clusterable. As a consequence, our results extend to clustering mixtures of arbitrary affine transforms of the uniform distribution on the $d$-dimensional unit sphere. Even the information theoretic clusterability of separated distributions satisfying these two analytic assumptions was not known prior to our work and is likely to be of independent interest. Our algorithms build on the recent sequence of works relying on certifiable anti-concentration first introduced in [KKK'19,RY'20]. Our techniques expand the sum-of-squares toolkit to show robust certifiability of TV-separated Gaussian clusters in data. This involves giving a low-degree sum-of-squares proof of statements that relate parameter (i.e. mean and covariances) distance to total variation distance by relying only on hypercontractivity and anti-concentration.

List-Decodable Subspace Recovery via Sum-of-Squares

We give the first efficient algorithm for the problem of list-decodable subspace recovery. Our algorithm takes input $n$ samples $\alpha n$ ($\alpha\ll 1/2$) are generated i.i.d. from Gaussian distribution $\mathcal{N}(0,\Sigma_*)$ on $\mathbb{R}^d$ with covariance $\Sigma_*$ of rank $r$ and the rest are arbitrary, potentially adversarial outliers. It outputs a list of $O(1/\alpha)$ projection matrices guaranteed to contain a projection matrix $\Pi$ such that $\|\Pi-\Pi_*\|_F^2 = \kappa^4 \log (r) \tilde{O}(1/\alpha^2)$, where $\tilde{O}$ hides polylogarithmic factors in $1/\alpha$. Here, $\Pi_*$ is the projection matrix to the range space of $\Sigma_*$. The algorithm needs $n=d^{\log (r \kappa) \tilde{O}(1/\alpha^2)}$ samples and runs in time $n^{\log (r \kappa) \tilde{O}(1/\alpha^4)}$ time where $\kappa$ is the ratio of the largest to smallest non-zero eigenvalues of $\Sigma_*$. Our algorithm builds on the recently developed framework for list-decodable learning via the sum-of-squares (SoS) method [KKK'19, RY'20] with some key technical and conceptual advancements. Our key conceptual contribution involves showing a (SoS "certified") lower bound on the eigenvalues of covariances of arbitrary small subsamples of an i.i.d. sample of a certifiably anti-concentrated distribution. One of our key technical contributions gives a new method that allows error reduction "within SoS" with only a logarithmic cost in the exponent in the running time (in contrast to polynomial cost in [KKK'19, RY'20]. In a concurrent and independent work, Raghavendra and Yau proved related results for list-decodable subspace recovery [RY'20].

Nearly Tight Bounds on $\ell_1$ Approximation of Self-Bounding Functions

We study the complexity of learning and approximation of self-bounding functions over the uniform distribution on the Boolean hypercube ${0,1}^n$. Informally, a function $f:{0,1}^n \rightarrow \mathbb{R}$ is self-bounding if for every $x \in {0,1}^n$, $f(x)$ upper bounds the sum of all the $n$ marginal decreases in the value of the function at $x$. Self-bounding functions include such well-known classes of functions as submodular and fractionally-subadditive (XOS) functions. They were introduced by Boucheron et al. in the context of concentration of measure inequalities. Our main result is a nearly tight $\ell_1$-approximation of self-bounding functions by low-degree juntas. Specifically, all self-bounding functions can be $\epsilon$-approximated in $\ell_1$ by a polynomial of degree $\tilde{O}(1/\epsilon)$ over $2^{\tilde{O}(1/\epsilon)}$ variables. We show that both the degree and junta-size are optimal up to logarithmic terms. Previous techniques considered stronger $\ell_2$ approximation and proved nearly tight bounds of $\Theta(1/\epsilon^{2})$ on the degree and $2^{\Theta(1/\epsilon^2)}$ on the number of variables. Our bounds rely on the analysis of noise stability of self-bounding functions together with a stronger connection between noise stability and $\ell_1$ approximation by low-degree polynomials. This technique can also be used to get tighter bounds on $\ell_1$ approximation by low-degree polynomials and faster learning algorithm for halfspaces. These results lead to improved and in several cases almost tight bounds for PAC and agnostic learning of self-bounding functions relative to the uniform distribution. In particular, assuming hardness of learning juntas, we show that PAC and agnostic learning of self-bounding functions have complexity of $n^{\tilde{\Theta}(1/\epsilon)}$.

Agnostic Learning of Disjunctions on Symmetric Distributions

We consider the problem of approximating and learning disjunctions (or equivalently, conjunctions) on symmetric distributions over $\{0,1\}^n$. Symmetric distributions are distributions whose PDF is invariant under any permutation of the variables. We give a simple proof that for every symmetric distribution $\mathcal{D}$, there exists a set of $n^{O(\log{(1/\epsilon)})}$ functions $\mathcal{S}$, such that for every disjunction $c$, there is function $p$, expressible as a linear combination of functions in $\mathcal{S}$, such that $p$ $\epsilon$-approximates $c$ in $\ell_1$ distance on $\mathcal{D}$ or $\mathbf{E}_{x \sim \mathcal{D}}[ |c(x)-p(x)|] \leq \epsilon$. This directly gives an agnostic learning algorithm for disjunctions on symmetric distributions that runs in time $n^{O( \log{(1/\epsilon)})}$. The best known previous bound is $n^{O(1/\epsilon^4)}$ and follows from approximation of the more general class of halfspaces (Wimmer, 2010). We also show that there exists a symmetric distribution $\mathcal{D}$, such that the minimum degree of a polynomial that $1/3$-approximates the disjunction of all $n$ variables is $\ell_1$ distance on $\mathcal{D}$ is $\Omega( \sqrt{n})$. Therefore the learning result above cannot be achieved via $\ell_1$-regression with a polynomial basis used in most other agnostic learning algorithms. Our technique also gives a simple proof that for any product distribution $\mathcal{D}$ and every disjunction $c$, there exists a polynomial $p$ of degree $O(\log{(1/\epsilon)})$ such that $p$ $\epsilon$-approximates $c$ in $\ell_1$ distance on $\mathcal{D}$. This was first proved by Blais et al. (2008) via a more involved argument.

Learning Coverage Functions and Private Release of Marginals

We study the problem of approximating and learning coverage functions. A function $c: 2^{[n]} \rightarrow \mathbf{R}^{+}$ is a coverage function, if there exists a universe $U$ with non-negative weights $w(u)$ for each $u \in U$ and subsets $A_1, A_2, \ldots, A_n$ of $U$ such that $c(S) = \sum_{u \in \cup_{i \in S} A_i} w(u)$. Alternatively, coverage functions can be described as non-negative linear combinations of monotone disjunctions. They are a natural subclass of submodular functions and arise in a number of applications. We give an algorithm that for any $\gamma,\delta>0$, given random and uniform examples of an unknown coverage function $c$, finds a function $h$ that approximates $c$ within factor $1+\gamma$ on all but $\delta$-fraction of the points in time $poly(n,1/\gamma,1/\delta)$. This is the first fully-polynomial algorithm for learning an interesting class of functions in the demanding PMAC model of Balcan and Harvey (2011). Our algorithms are based on several new structural properties of coverage functions. Using the results in (Feldman and Kothari, 2014), we also show that coverage functions are learnable agnostically with excess $\ell_1$-error $\epsilon$ over all product and symmetric distributions in time $n^{\log(1/\epsilon)}$. In contrast, we show that, without assumptions on the distribution, learning coverage functions is at least as hard as learning polynomial-size disjoint DNF formulas, a class of functions for which the best known algorithm runs in time $2^{\tilde{O}(n^{1/3})}$ (Klivans and Servedio, 2004). As an application of our learning results, we give simple differentially-private algorithms for releasing monotone conjunction counting queries with low average error. In particular, for any $k \leq n$, we obtain private release of $k$-way marginals with average error $\bar{\alpha}$ in time $n^{O(\log(1/\bar{\alpha}))}$.

Representation, Approximation and Learning of Submodular Functions Using Low-rank Decision Trees

We study the complexity of approximate representation and learning of submodular functions over the uniform distribution on the Boolean hypercube $\{0,1\}^n$. Our main result is the following structural theorem: any submodular function is $\epsilon$-close in $\ell_2$ to a real-valued decision tree (DT) of depth $O(1/\epsilon^2)$. This immediately implies that any submodular function is $\epsilon$-close to a function of at most $2^{O(1/\epsilon^2)}$ variables and has a spectral $\ell_1$ norm of $2^{O(1/\epsilon^2)}$. It also implies the closest previous result that states that submodular functions can be approximated by polynomials of degree $O(1/\epsilon^2)$ (Cheraghchi et al., 2012). Our result is proved by constructing an approximation of a submodular function by a DT of rank $4/\epsilon^2$ and a proof that any rank-$r$ DT can be $\epsilon$-approximated by a DT of depth $\frac{5}{2}(r+\log(1/\epsilon))$. We show that these structural results can be exploited to give an attribute-efficient PAC learning algorithm for submodular functions running in time $\tilde{O}(n^2) \cdot 2^{O(1/\epsilon^{4})}$. The best previous algorithm for the problem requires $n^{O(1/\epsilon^{2})}$ time and examples (Cheraghchi et al., 2012) but works also in the agnostic setting. In addition, we give improved learning algorithms for a number of related settings. We also prove that our PAC and agnostic learning algorithms are essentially optimal via two lower bounds: (1) an information-theoretic lower bound of $2^{\Omega(1/\epsilon^{2/3})}$ on the complexity of learning monotone submodular functions in any reasonable model; (2) computational lower bound of $n^{\Omega(1/\epsilon^{2/3})}$ based on a reduction to learning of sparse parities with noise, widely-believed to be intractable. These are the first lower bounds for learning of submodular functions over the uniform distribution.

Differentially Private Online Learning

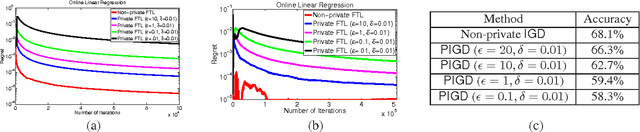
In this paper, we consider the problem of preserving privacy in the online learning setting. We study the problem in the online convex programming (OCP) framework---a popular online learning setting with several interesting theoretical and practical implications---while using differential privacy as the formal privacy measure. For this problem, we distill two critical attributes that a private OCP algorithm should have in order to provide reasonable privacy as well as utility guarantees: 1) linearly decreasing sensitivity, i.e., as new data points arrive their effect on the learning model decreases, 2) sub-linear regret bound---regret bound is a popular goodness/utility measure of an online learning algorithm. Given an OCP algorithm that satisfies these two conditions, we provide a general framework to convert the given algorithm into a privacy preserving OCP algorithm with good (sub-linear) regret. We then illustrate our approach by converting two popular online learning algorithms into their differentially private variants while guaranteeing sub-linear regret ($O(\sqrt{T})$). Next, we consider the special case of online linear regression problems, a practically important class of online learning problems, for which we generalize an approach by Dwork et al. to provide a differentially private algorithm with just $O(\log^{1.5} T)$ regret. Finally, we show that our online learning framework can be used to provide differentially private algorithms for offline learning as well. For the offline learning problem, our approach obtains better error bounds as well as can handle larger class of problems than the existing state-of-the-art methods Chaudhuri et al.

Submodular Functions Are Noise Stable

We show that all non-negative submodular functions have high {\em noise-stability}. As a consequence, we obtain a polynomial-time learning algorithm for this class with respect to any product distribution on $\{-1,1\}^n$ (for any constant accuracy parameter $\epsilon$). Our algorithm also succeeds in the agnostic setting. Previous work on learning submodular functions required either query access or strong assumptions about the types of submodular functions to be learned (and did not hold in the agnostic setting).