Do LLMs dream of elephants (when told not to)? Latent concept association and associative memory in transformers

Large Language Models (LLMs) have the capacity to store and recall facts. Through experimentation with open-source models, we observe that this ability to retrieve facts can be easily manipulated by changing contexts, even without altering their factual meanings. These findings highlight that LLMs might behave like an associative memory model where certain tokens in the contexts serve as clues to retrieving facts. We mathematically explore this property by studying how transformers, the building blocks of LLMs, can complete such memory tasks. We study a simple latent concept association problem with a one-layer transformer and we show theoretically and empirically that the transformer gathers information using self-attention and uses the value matrix for associative memory.

Efficient Certificates of Anti-Concentration Beyond Gaussians

A set of high dimensional points $X=\{x_1, x_2,\ldots, x_n\} \subset R^d$ in isotropic position is said to be $\delta$-anti concentrated if for every direction $v$, the fraction of points in $X$ satisfying $|\langle x_i,v \rangle |\leq \delta$ is at most $O(\delta)$. Motivated by applications to list-decodable learning and clustering, recent works have considered the problem of constructing efficient certificates of anti-concentration in the average case, when the set of points $X$ corresponds to samples from a Gaussian distribution. Their certificates played a crucial role in several subsequent works in algorithmic robust statistics on list-decodable learning and settling the robust learnability of arbitrary Gaussian mixtures, yet remain limited to rotationally invariant distributions. This work presents a new (and arguably the most natural) formulation for anti-concentration. Using this formulation, we give quasi-polynomial time verifiable sum-of-squares certificates of anti-concentration that hold for a wide class of non-Gaussian distributions including anti-concentrated bounded product distributions and uniform distributions over $L_p$ balls (and their affine transformations). Consequently, our method upgrades and extends results in algorithmic robust statistics e.g., list-decodable learning and clustering, to such distributions. Our approach constructs a canonical integer program for anti-concentration and analysis a sum-of-squares relaxation of it, independent of the intended application. We rely on duality and analyze a pseudo-expectation on large subsets of the input points that take a small value in some direction. Our analysis uses the method of polynomial reweightings to reduce the problem to analyzing only analytically dense or sparse directions.

On the Origins of Linear Representations in Large Language Models

Recent works have argued that high-level semantic concepts are encoded "linearly" in the representation space of large language models. In this work, we study the origins of such linear representations. To that end, we introduce a simple latent variable model to abstract and formalize the concept dynamics of the next token prediction. We use this formalism to show that the next token prediction objective (softmax with cross-entropy) and the implicit bias of gradient descent together promote the linear representation of concepts. Experiments show that linear representations emerge when learning from data matching the latent variable model, confirming that this simple structure already suffices to yield linear representations. We additionally confirm some predictions of the theory using the LLaMA-2 large language model, giving evidence that the simplified model yields generalizable insights.

Learning Interpretable Concepts: Unifying Causal Representation Learning and Foundation Models

To build intelligent machine learning systems, there are two broad approaches. One approach is to build inherently interpretable models, as endeavored by the growing field of causal representation learning. The other approach is to build highly-performant foundation models and then invest efforts into understanding how they work. In this work, we relate these two approaches and study how to learn human-interpretable concepts from data. Weaving together ideas from both fields, we formally define a notion of concepts and show that they can be provably recovered from diverse data. Experiments on synthetic data and large language models show the utility of our unified approach.

An Interventional Perspective on Identifiability in Gaussian LTI Systems with Independent Component Analysis

We investigate the relationship between system identification and intervention design in dynamical systems. While previous research demonstrated how identifiable representation learning methods, such as Independent Component Analysis (ICA), can reveal cause-effect relationships, it relied on a passive perspective without considering how to collect data. Our work shows that in Gaussian Linear Time-Invariant (LTI) systems, the system parameters can be identified by introducing diverse intervention signals in a multi-environment setting. By harnessing appropriate diversity assumptions motivated by the ICA literature, our findings connect experiment design and representational identifiability in dynamical systems. We corroborate our findings on synthetic and (simulated) physical data. Additionally, we show that Hidden Markov Models, in general, and (Gaussian) LTI systems, in particular, fulfil a generalization of the Causal de Finetti theorem with continuous parameters.

Learning Linear Causal Representations from Interventions under General Nonlinear Mixing

We study the problem of learning causal representations from unknown, latent interventions in a general setting, where the latent distribution is Gaussian but the mixing function is completely general. We prove strong identifiability results given unknown single-node interventions, i.e., without having access to the intervention targets. This generalizes prior works which have focused on weaker classes, such as linear maps or paired counterfactual data. This is also the first instance of causal identifiability from non-paired interventions for deep neural network embeddings. Our proof relies on carefully uncovering the high-dimensional geometric structure present in the data distribution after a non-linear density transformation, which we capture by analyzing quadratic forms of precision matrices of the latent distributions. Finally, we propose a contrastive algorithm to identify the latent variables in practice and evaluate its performance on various tasks.

Nonlinear Random Matrices and Applications to the Sum of Squares Hierarchy

We develop new tools in the theory of nonlinear random matrices and apply them to study the performance of the Sum of Squares (SoS) hierarchy on average-case problems. The SoS hierarchy is a powerful optimization technique that has achieved tremendous success for various problems in combinatorial optimization, robust statistics and machine learning. It's a family of convex relaxations that lets us smoothly trade off running time for approximation guarantees. In recent works, it's been shown to be extremely useful for recovering structure in high dimensional noisy data. It also remains our best approach towards refuting the notorious Unique Games Conjecture. In this work, we analyze the performance of the SoS hierarchy on fundamental problems stemming from statistics, theoretical computer science and statistical physics. In particular, we show subexponential-time SoS lower bounds for the problems of the Sherrington-Kirkpatrick Hamiltonian, Planted Slightly Denser Subgraph, Tensor Principal Components Analysis and Sparse Principal Components Analysis. These SoS lower bounds involve analyzing large random matrices, wherein lie our main contributions. These results offer strong evidence for the truth of and insight into the low-degree likelihood ratio hypothesis, an important conjecture that predicts the power of bounded-time algorithms for hypothesis testing. We also develop general-purpose tools for analyzing the behavior of random matrices which are functions of independent random variables. Towards this, we build on and generalize the matrix variant of the Efron-Stein inequalities. In particular, our general theorem on matrix concentration recovers various results that have appeared in the literature. We expect these random matrix theory ideas to have other significant applications.

Concentration of polynomial random matrices via Efron-Stein inequalities

Analyzing concentration of large random matrices is a common task in a wide variety of fields. Given independent random variables, many tools are available to analyze random matrices whose entries are linear in the variables, e.g. the matrix-Bernstein inequality. However, in many applications, we need to analyze random matrices whose entries are polynomials in the variables. These arise naturally in the analysis of spectral algorithms, e.g., Hopkins et al. [STOC 2016], Moitra-Wein [STOC 2019]; and in lower bounds for semidefinite programs based on the Sum of Squares hierarchy, e.g. Barak et al. [FOCS 2016], Jones et al. [FOCS 2021]. In this work, we present a general framework to obtain such bounds, based on the matrix Efron-Stein inequalities developed by Paulin-Mackey-Tropp [Annals of Probability 2016]. The Efron-Stein inequality bounds the norm of a random matrix by the norm of another simpler (but still random) matrix, which we view as arising by "differentiating" the starting matrix. By recursively differentiating, our framework reduces the main task to analyzing far simpler matrices. For Rademacher variables, these simpler matrices are in fact deterministic and hence, analyzing them is far easier. For general non-Rademacher variables, the task reduces to scalar concentration, which is much easier. Moreover, in the setting of polynomial matrices, our results generalize the work of Paulin-Mackey-Tropp. Using our basic framework, we recover known bounds in the literature for simple "tensor networks" and "dense graph matrices". Using our general framework, we derive bounds for "sparse graph matrices", which were obtained only recently by Jones et al. [FOCS 2021] using a nontrivial application of the trace power method, and was a core component in their work. We expect our framework to be helpful for other applications involving concentration phenomena for nonlinear random matrices.

Analyzing Robustness of End-to-End Neural Models for Automatic Speech Recognition

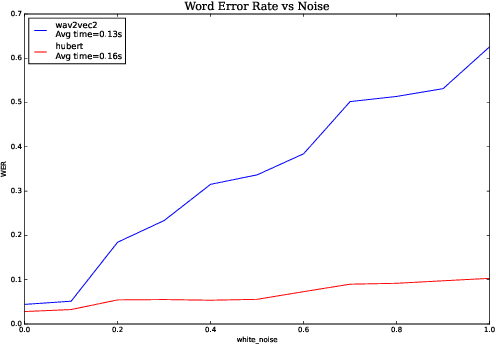
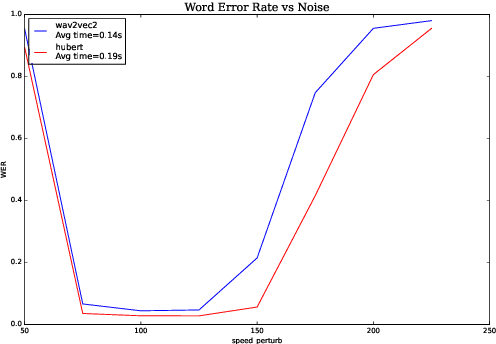
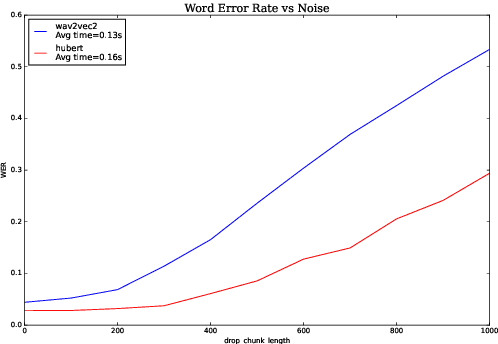
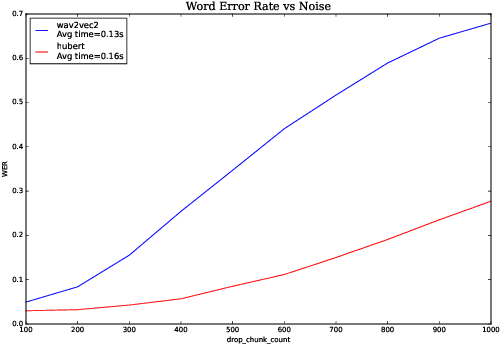
We investigate robustness properties of pre-trained neural models for automatic speech recognition. Real life data in machine learning is usually very noisy and almost never clean, which can be attributed to various factors depending on the domain, e.g. outliers, random noise and adversarial noise. Therefore, the models we develop for various tasks should be robust to such kinds of noisy data, which led to the thriving field of robust machine learning. We consider this important issue in the setting of automatic speech recognition. With the increasing popularity of pre-trained models, it's an important question to analyze and understand the robustness of such models to noise. In this work, we perform a robustness analysis of the pre-trained neural models wav2vec2, HuBERT and DistilHuBERT on the LibriSpeech and TIMIT datasets. We use different kinds of noising mechanisms and measure the model performances as quantified by the inference time and the standard Word Error Rate metric. We also do an in-depth layer-wise analysis of the wav2vec2 model when injecting noise in between layers, enabling us to predict at a high level what each layer learns. Finally for this model, we visualize the propagation of errors across the layers and compare how it behaves on clean versus noisy data. Our experiments conform the predictions of Pasad et al. [2021] and also raise interesting directions for future work.

Identifiability of deep generative models under mixture priors without auxiliary information

We prove identifiability of a broad class of deep latent variable models that (a) have universal approximation capabilities and (b) are the decoders of variational autoencoders that are commonly used in practice. Unlike existing work, our analysis does not require weak supervision, auxiliary information, or conditioning in the latent space. Recently, there has been a surge of works studying identifiability of such models. In these works, the main assumption is that along with the data, an auxiliary variable $u$ (also known as side information) is observed as well. At the same time, several works have empirically observed that this doesn't seem to be necessary in practice. In this work, we explain this behavior by showing that for a broad class of generative (i.e. unsupervised) models with universal approximation capabilities, the side information $u$ is not necessary: We prove identifiability of the entire generative model where we do not observe $u$ and only observe the data $x$. The models we consider are tightly connected with autoencoder architectures used in practice that leverage mixture priors in the latent space and ReLU/leaky-ReLU activations in the encoder. Our main result is an identifiability hierarchy that significantly generalizes previous work and exposes how different assumptions lead to different "strengths" of identifiability. For example, our weakest result establishes (unsupervised) identifiability up to an affine transformation, which already improves existing work. It's well known that these models have universal approximation capabilities and moreover, they have been extensively used in practice to learn representations of data.