Deep sequence models tend to memorize geometrically; it is unclear why

In sequence modeling, the parametric memory of atomic facts has been predominantly abstracted as a brute-force lookup of co-occurrences between entities. We contrast this associative view against a geometric view of how memory is stored. We begin by isolating a clean and analyzable instance of Transformer reasoning that is incompatible with memory as strictly a storage of the local co-occurrences specified during training. Instead, the model must have somehow synthesized its own geometry of atomic facts, encoding global relationships between all entities, including non-co-occurring ones. This in turn has simplified a hard reasoning task involving an $\ell$-fold composition into an easy-to-learn 1-step geometric task. From this phenomenon, we extract fundamental aspects of neural embedding geometries that are hard to explain. We argue that the rise of such a geometry, despite optimizing over mere local associations, cannot be straightforwardly attributed to typical architectural or optimizational pressures. Counterintuitively, an elegant geometry is learned even when it is not more succinct than a brute-force lookup of associations. Then, by analyzing a connection to Node2Vec, we demonstrate how the geometry stems from a spectral bias that -- in contrast to prevailing theories -- indeed arises naturally despite the lack of various pressures. This analysis also points to practitioners a visible headroom to make Transformer memory more strongly geometric. We hope the geometric view of parametric memory encourages revisiting the default intuitions that guide researchers in areas like knowledge acquisition, capacity, discovery and unlearning.

Outliers with Opposing Signals Have an Outsized Effect on Neural Network Optimization

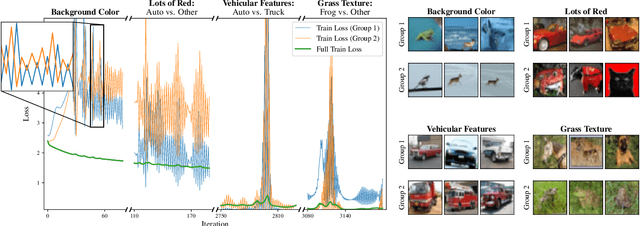
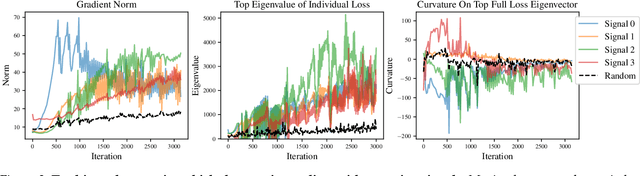
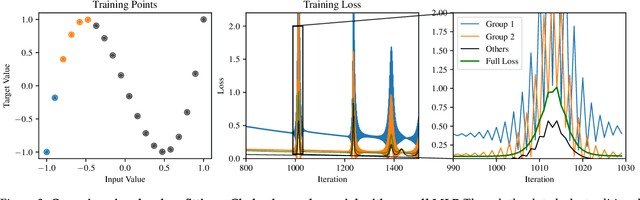
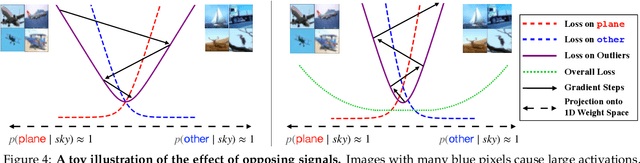
We identify a new phenomenon in neural network optimization which arises from the interaction of depth and a particular heavy-tailed structure in natural data. Our result offers intuitive explanations for several previously reported observations about network training dynamics. In particular, it implies a conceptually new cause for progressive sharpening and the edge of stability; we also highlight connections to other concepts in optimization and generalization including grokking, simplicity bias, and Sharpness-Aware Minimization. Experimentally, we demonstrate the significant influence of paired groups of outliers in the training data with strong opposing signals: consistent, large magnitude features which dominate the network output throughout training and provide gradients which point in opposite directions. Due to these outliers, early optimization enters a narrow valley which carefully balances the opposing groups; subsequent sharpening causes their loss to rise rapidly, oscillating between high on one group and then the other, until the overall loss spikes. We describe how to identify these groups, explore what sets them apart, and carefully study their effect on the network's optimization and behavior. We complement these experiments with a mechanistic explanation on a toy example of opposing signals and a theoretical analysis of a two-layer linear network on a simple model. Our finding enables new qualitative predictions of training behavior which we confirm experimentally. It also provides a new lens through which to study and improve modern training practices for stochastic optimization, which we highlight via a case study of Adam versus SGD.

One-Shot Strategic Classification Under Unknown Costs

A primary goal in strategic classification is to learn decision rules which are robust to strategic input manipulation. Earlier works assume that strategic responses are known; while some recent works address the important challenge of unknown responses, they exclusively study sequential settings which allow multiple model deployments over time. But there are many domains$\unicode{x2014}$particularly in public policy, a common motivating use-case$\unicode{x2014}$where multiple deployments are unrealistic, or where even a single bad round is undesirable. To address this gap, we initiate the study of strategic classification under unknown responses in the one-shot setting, which requires committing to a single classifier once. Focusing on the users' cost function as the source of uncertainty, we begin by proving that for a broad class of costs, even a small mis-estimation of the true cost can entail arbitrarily low accuracy in the worst case. In light of this, we frame the one-shot task as a minimax problem, with the goal of identifying the classifier with the smallest worst-case risk over an uncertainty set of possible costs. Our main contribution is efficient algorithms for both the full-batch and stochastic settings, which we prove converge (offline) to the minimax optimal solution at the dimension-independent rate of $\tilde{\mathcal{O}}(T^{-\frac{1}{2}})$. Our analysis reveals important structure stemming from the strategic nature of user responses, particularly the importance of dual norm regularization with respect to the cost function.

Identifying Representations for Intervention Extrapolation

The premise of identifiable and causal representation learning is to improve the current representation learning paradigm in terms of generalizability or robustness. Despite recent progress in questions of identifiability, more theoretical results demonstrating concrete advantages of these methods for downstream tasks are needed. In this paper, we consider the task of intervention extrapolation: predicting how interventions affect an outcome, even when those interventions are not observed at training time, and show that identifiable representations can provide an effective solution to this task even if the interventions affect the outcome non-linearly. Our setup includes an outcome Y, observed features X, which are generated as a non-linear transformation of latent features Z, and exogenous action variables A, which influence Z. The objective of intervention extrapolation is to predict how interventions on A that lie outside the training support of A affect Y. Here, extrapolation becomes possible if the effect of A on Z is linear and the residual when regressing Z on A has full support. As Z is latent, we combine the task of intervention extrapolation with identifiable representation learning, which we call Rep4Ex: we aim to map the observed features X into a subspace that allows for non-linear extrapolation in A. We show using Wiener's Tauberian theorem that the hidden representation is identifiable up to an affine transformation in Z-space, which is sufficient for intervention extrapolation. The identifiability is characterized by a novel constraint describing the linearity assumption of A on Z. Based on this insight, we propose a method that enforces the linear invariance constraint and can be combined with any type of autoencoder. We validate our theoretical findings through synthetic experiments and show that our approach succeeds in predicting the effects of unseen interventions.

Learning Linear Causal Representations from Interventions under General Nonlinear Mixing

We study the problem of learning causal representations from unknown, latent interventions in a general setting, where the latent distribution is Gaussian but the mixing function is completely general. We prove strong identifiability results given unknown single-node interventions, i.e., without having access to the intervention targets. This generalizes prior works which have focused on weaker classes, such as linear maps or paired counterfactual data. This is also the first instance of causal identifiability from non-paired interventions for deep neural network embeddings. Our proof relies on carefully uncovering the high-dimensional geometric structure present in the data distribution after a non-linear density transformation, which we capture by analyzing quadratic forms of precision matrices of the latent distributions. Finally, we propose a contrastive algorithm to identify the latent variables in practice and evaluate its performance on various tasks.

(Almost) Provable Error Bounds Under Distribution Shift via Disagreement Discrepancy

We derive an (almost) guaranteed upper bound on the error of deep neural networks under distribution shift using unlabeled test data. Prior methods either give bounds that are vacuous in practice or give estimates that are accurate on average but heavily underestimate error for a sizeable fraction of shifts. In particular, the latter only give guarantees based on complex continuous measures such as test calibration -- which cannot be identified without labels -- and are therefore unreliable. Instead, our bound requires a simple, intuitive condition which is well justified by prior empirical works and holds in practice effectively 100% of the time. The bound is inspired by $\mathcal{H}\Delta\mathcal{H}$-divergence but is easier to evaluate and substantially tighter, consistently providing non-vacuous guarantees. Estimating the bound requires optimizing one multiclass classifier to disagree with another, for which some prior works have used sub-optimal proxy losses; we devise a "disagreement loss" which is theoretically justified and performs better in practice. We expect this loss can serve as a drop-in replacement for future methods which require maximizing multiclass disagreement. Across a wide range of benchmarks, our method gives valid error bounds while achieving average accuracy comparable to competitive estimation baselines. Code is publicly available at https://github.com/erosenfeld/disagree_discrep .

APE: Aligning Pretrained Encoders to Quickly Learn Aligned Multimodal Representations

Recent advances in learning aligned multimodal representations have been primarily driven by training large neural networks on massive, noisy paired-modality datasets. In this work, we ask whether it is possible to achieve similar results with substantially less training time and data. We achieve this by taking advantage of existing pretrained unimodal encoders and careful curation of alignment data relevant to the downstream task of interest. We study a natural approach to aligning existing encoders via small auxiliary functions, and we find that this method is competitive with (or outperforms) state of the art in many settings while being less prone to overfitting, less costly to train, and more robust to distribution shift. With a properly chosen alignment distribution, our method surpasses prior state of the art for ImageNet zero-shot classification on public data while using two orders of magnitude less time and data and training 77% fewer parameters.

Domain-Adjusted Regression or: ERM May Already Learn Features Sufficient for Out-of-Distribution Generalization

A common explanation for the failure of deep networks to generalize out-of-distribution is that they fail to recover the "correct" features. Focusing on the domain generalization setting, we challenge this notion with a simple experiment which suggests that ERM already learns sufficient features and that the current bottleneck is not feature learning, but robust regression. We therefore argue that devising simpler methods for learning predictors on existing features is a promising direction for future research. Towards this end, we introduce Domain-Adjusted Regression (DARE), a convex objective for learning a linear predictor that is provably robust under a new model of distribution shift. Rather than learning one function, DARE performs a domain-specific adjustment to unify the domains in a canonical latent space and learns to predict in this space. Under a natural model, we prove that the DARE solution is the minimax-optimal predictor for a constrained set of test distributions. Further, we provide the first finite-environment convergence guarantee to the minimax risk, improving over existing results which show a "threshold effect". Evaluated on finetuned features, we find that DARE compares favorably to prior methods, consistently achieving equal or better performance.

Analyzing and Improving the Optimization Landscape of Noise-Contrastive Estimation

Noise-contrastive estimation (NCE) is a statistically consistent method for learning unnormalized probabilistic models. It has been empirically observed that the choice of the noise distribution is crucial for NCE's performance. However, such observations have never been made formal or quantitative. In fact, it is not even clear whether the difficulties arising from a poorly chosen noise distribution are statistical or algorithmic in nature. In this work, we formally pinpoint reasons for NCE's poor performance when an inappropriate noise distribution is used. Namely, we prove these challenges arise due to an ill-behaved (more precisely, flat) loss landscape. To address this, we introduce a variant of NCE called "eNCE" which uses an exponential loss and for which normalized gradient descent addresses the landscape issues provably when the target and noise distributions are in a given exponential family.

Iterative Feature Matching: Toward Provable Domain Generalization with Logarithmic Environments

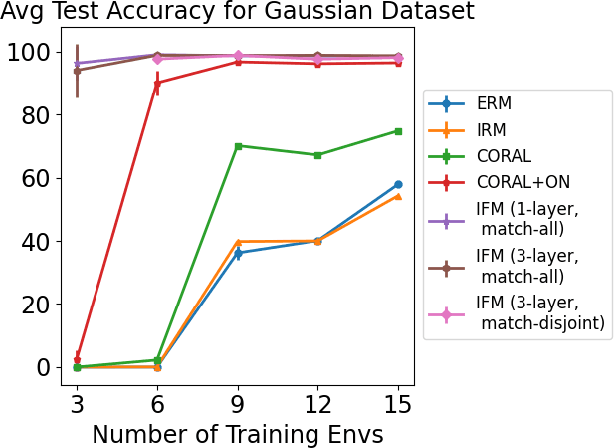
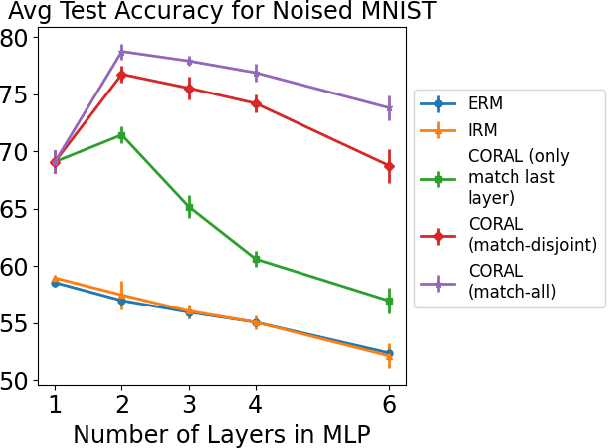
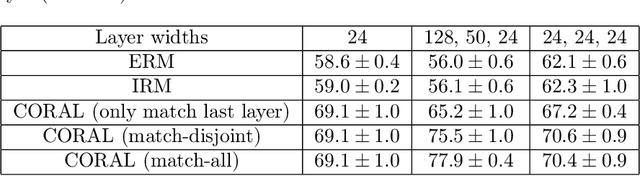
Domain generalization aims at performing well on unseen test environments with data from a limited number of training environments. Despite a proliferation of proposal algorithms for this task, assessing their performance, both theoretically and empirically is still very challenging. Moreover, recent approaches such as Invariant Risk Minimization (IRM) require a prohibitively large number of training environments - linear in the dimension of the spurious feature space $d_s$ - even on simple data models like the one proposed by [Rosenfeld et al., 2021]. Under a variant of this model, we show that both ERM and IRM cannot generalize with $o(d_s)$ environments. We then present a new algorithm based on performing iterative feature matching that is guaranteed with high probability to yield a predictor that generalizes after seeing only $O(\log{d_s})$ environments.