Victor Veitch
Does Editing Provide Evidence for Localization?
Feb 19, 2025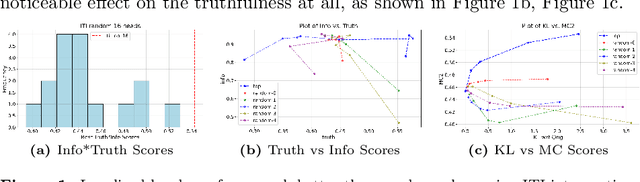
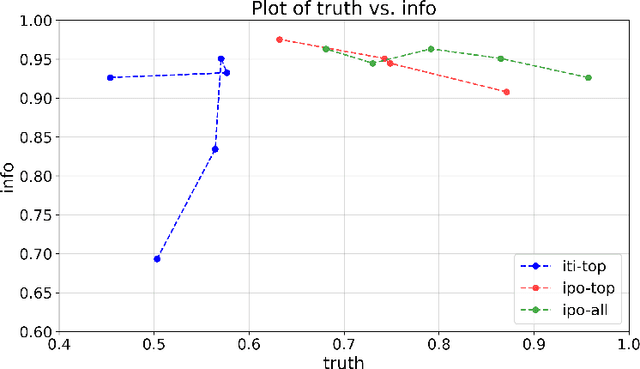
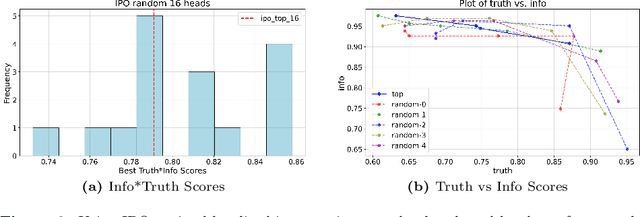
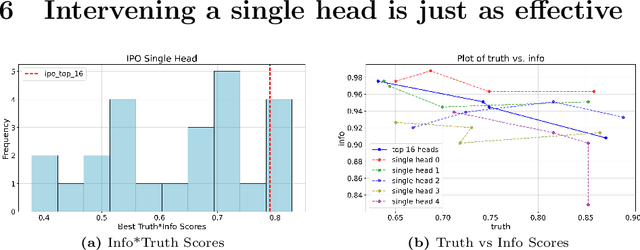
Abstract:A basic aspiration for interpretability research in large language models is to "localize" semantically meaningful behaviors to particular components within the LLM. There are various heuristics for finding candidate locations within the LLM. Once a candidate localization is found, it can be assessed by editing the internal representations at the corresponding localization and checking whether this induces model behavior that is consistent with the semantic interpretation of the localization. The question we address here is: how strong is the evidence provided by such edits? To evaluate the localization claim, we want to assess the effect of the optimal intervention at a particular location. The key new technical tool is a way of adapting LLM alignment techniques to find such optimal localized edits. With this tool in hand, we give an example where the edit-based evidence for localization appears strong, but where localization clearly fails. Indeed, we find that optimal edits at random localizations can be as effective as aligning the full model. In aggregate, our results suggest that merely observing that localized edits induce targeted changes in behavior provides little to no evidence that these locations actually encode the target behavior.
RATE: Score Reward Models with Imperfect Rewrites of Rewrites
Oct 15, 2024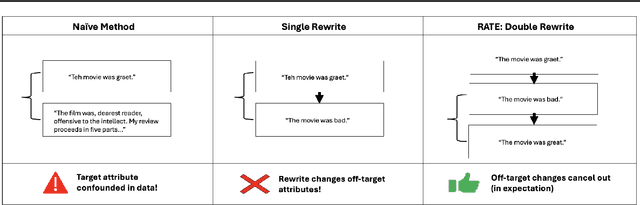

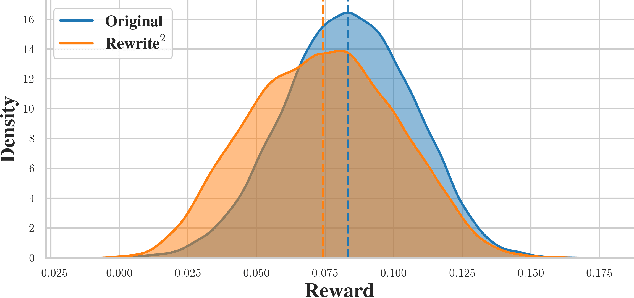
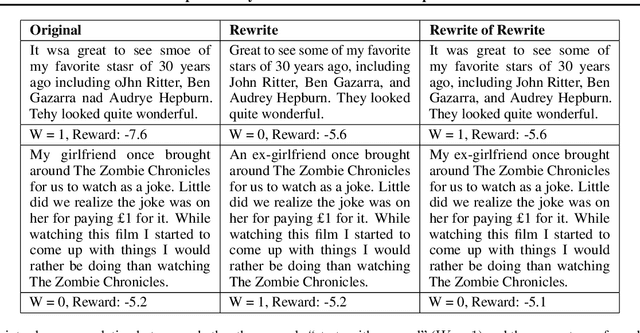
Abstract:This paper concerns the evaluation of reward models used in language modeling. A reward model is a function that takes a prompt and a response and assigns a score indicating how good that response is for the prompt. A key challenge is that reward models are usually imperfect proxies for actual preferences. For example, we may worry that a model trained to reward helpfulness learns to instead prefer longer responses. In this paper, we develop an evaluation method, RATE (Rewrite-based Attribute Treatment Estimators), that allows us to measure the causal effect of a given attribute of a response (e.g., length) on the reward assigned to that response. The core idea is to use large language models to rewrite responses to produce imperfect counterfactuals, and to adjust for rewriting error by rewriting twice. We show that the RATE estimator is consistent under reasonable assumptions. We demonstrate the effectiveness of RATE on synthetic and real-world data, showing that it can accurately estimate the effect of a given attribute on the reward model.
The Geometry of Categorical and Hierarchical Concepts in Large Language Models
Jun 03, 2024Abstract:Understanding how semantic meaning is encoded in the representation spaces of large language models is a fundamental problem in interpretability. In this paper, we study the two foundational questions in this area. First, how are categorical concepts, such as {'mammal', 'bird', 'reptile', 'fish'}, represented? Second, how are hierarchical relations between concepts encoded? For example, how is the fact that 'dog' is a kind of 'mammal' encoded? We show how to extend the linear representation hypothesis to answer these questions. We find a remarkably simple structure: simple categorical concepts are represented as simplices, hierarchically related concepts are orthogonal in a sense we make precise, and (in consequence) complex concepts are represented as polytopes constructed from direct sums of simplices, reflecting the hierarchical structure. We validate these theoretical results on the Gemma large language model, estimating representations for 957 hierarchically related concepts using data from WordNet.
BoNBoN Alignment for Large Language Models and the Sweetness of Best-of-n Sampling
Jun 02, 2024Abstract:This paper concerns the problem of aligning samples from large language models to human preferences using best-of-$n$ sampling, where we draw $n$ samples, rank them, and return the best one. We consider two fundamental problems. First: what is the relationship between best-of-$n$ and approaches to alignment that train LLMs to output samples with a high expected reward (e.g., RLHF or DPO)? To answer this, we embed both the best-of-$n$ distribution and the sampling distributions learned by alignment procedures in a common class of tiltings of the base LLM distribution. We then show that, within this class, best-of-$n$ is essentially optimal in terms of the trade-off between win-rate against the base model vs KL distance from the base model. That is, best-of-$n$ is the best choice of alignment distribution if the goal is to maximize win rate. However, best-of-$n$ requires drawing $n$ samples for each inference, a substantial cost. To avoid this, the second problem we consider is how to fine-tune a LLM to mimic the best-of-$n$ sampling distribution. We derive BoNBoN Alignment to achieve this by exploiting the special structure of the best-of-$n$ distribution. Experiments show that BoNBoN alignment yields substantial improvements in producing a model that is preferred to the base policy while minimally affecting off-target aspects.
On the Origins of Linear Representations in Large Language Models
Mar 06, 2024Abstract:Recent works have argued that high-level semantic concepts are encoded "linearly" in the representation space of large language models. In this work, we study the origins of such linear representations. To that end, we introduce a simple latent variable model to abstract and formalize the concept dynamics of the next token prediction. We use this formalism to show that the next token prediction objective (softmax with cross-entropy) and the implicit bias of gradient descent together promote the linear representation of concepts. Experiments show that linear representations emerge when learning from data matching the latent variable model, confirming that this simple structure already suffices to yield linear representations. We additionally confirm some predictions of the theory using the LLaMA-2 large language model, giving evidence that the simplified model yields generalizable insights.
Transforming and Combining Rewards for Aligning Large Language Models
Feb 01, 2024Abstract:A common approach for aligning language models to human preferences is to first learn a reward model from preference data, and then use this reward model to update the language model. We study two closely related problems that arise in this approach. First, any monotone transformation of the reward model preserves preference ranking; is there a choice that is ``better'' than others? Second, we often wish to align language models to multiple properties: how should we combine multiple reward models? Using a probabilistic interpretation of the alignment procedure, we identify a natural choice for transformation for (the common case of) rewards learned from Bradley-Terry preference models. This derived transformation has two important properties. First, it emphasizes improving poorly-performing outputs, rather than outputs that already score well. This mitigates both underfitting (where some prompts are not improved) and reward hacking (where the model learns to exploit misspecification of the reward model). Second, it enables principled aggregation of rewards by linking summation to logical conjunction: the sum of transformed rewards corresponds to the probability that the output is ``good'' in all measured properties, in a sense we make precise. Experiments aligning language models to be both helpful and harmless using RLHF show substantial improvements over the baseline (non-transformed) approach.
The Linear Representation Hypothesis and the Geometry of Large Language Models
Nov 07, 2023Abstract:Informally, the 'linear representation hypothesis' is the idea that high-level concepts are represented linearly as directions in some representation space. In this paper, we address two closely related questions: What does "linear representation" actually mean? And, how do we make sense of geometric notions (e.g., cosine similarity or projection) in the representation space? To answer these, we use the language of counterfactuals to give two formalizations of "linear representation", one in the output (word) representation space, and one in the input (sentence) space. We then prove these connect to linear probing and model steering, respectively. To make sense of geometric notions, we use the formalization to identify a particular (non-Euclidean) inner product that respects language structure in a sense we make precise. Using this causal inner product, we show how to unify all notions of linear representation. In particular, this allows the construction of probes and steering vectors using counterfactual pairs. Experiments with LLaMA-2 demonstrate the existence of linear representations of concepts, the connection to interpretation and control, and the fundamental role of the choice of inner product.
Causal Context Connects Counterfactual Fairness to Robust Prediction and Group Fairness
Oct 30, 2023Abstract:Counterfactual fairness requires that a person would have been classified in the same way by an AI or other algorithmic system if they had a different protected class, such as a different race or gender. This is an intuitive standard, as reflected in the U.S. legal system, but its use is limited because counterfactuals cannot be directly observed in real-world data. On the other hand, group fairness metrics (e.g., demographic parity or equalized odds) are less intuitive but more readily observed. In this paper, we use $\textit{causal context}$ to bridge the gaps between counterfactual fairness, robust prediction, and group fairness. First, we motivate counterfactual fairness by showing that there is not necessarily a fundamental trade-off between fairness and accuracy because, under plausible conditions, the counterfactually fair predictor is in fact accuracy-optimal in an unbiased target distribution. Second, we develop a correspondence between the causal graph of the data-generating process and which, if any, group fairness metrics are equivalent to counterfactual fairness. Third, we show that in three common fairness contexts$\unicode{x2013}$measurement error, selection on label, and selection on predictors$\unicode{x2013}$counterfactual fairness is equivalent to demographic parity, equalized odds, and calibration, respectively. Counterfactual fairness can sometimes be tested by measuring relatively simple group fairness metrics.
Uncovering Meanings of Embeddings via Partial Orthogonality
Oct 26, 2023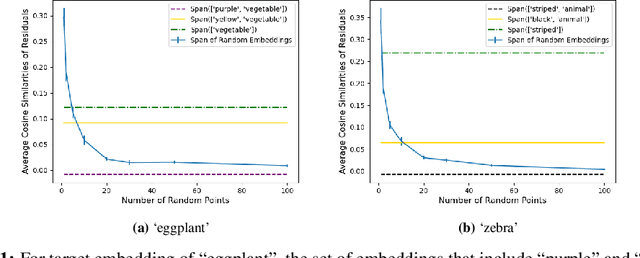

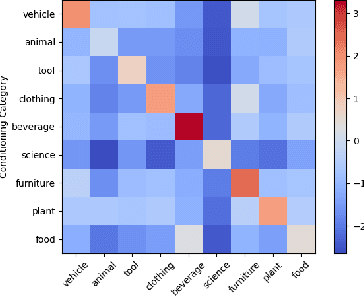

Abstract:Machine learning tools often rely on embedding text as vectors of real numbers. In this paper, we study how the semantic structure of language is encoded in the algebraic structure of such embeddings. Specifically, we look at a notion of ``semantic independence'' capturing the idea that, e.g., ``eggplant'' and ``tomato'' are independent given ``vegetable''. Although such examples are intuitive, it is difficult to formalize such a notion of semantic independence. The key observation here is that any sensible formalization should obey a set of so-called independence axioms, and thus any algebraic encoding of this structure should also obey these axioms. This leads us naturally to use partial orthogonality as the relevant algebraic structure. We develop theory and methods that allow us to demonstrate that partial orthogonality does indeed capture semantic independence. Complementary to this, we also introduce the concept of independence preserving embeddings where embeddings preserve the conditional independence structures of a distribution, and we prove the existence of such embeddings and approximations to them.
Concept Algebra for Text-Controlled Vision Models
Feb 07, 2023



Abstract:This paper concerns the control of text-guided generative models, where a user provides a natural language prompt and the model generates samples based on this input. Prompting is intuitive, general, and flexible. However, there are significant limitations: prompting can fail in surprising ways, and it is often unclear how to find a prompt that will elicit some desired target behavior. A core difficulty for developing methods to overcome these issues is that failures are know-it-when-you-see-it -- it's hard to fix bugs if you can't state precisely what the model should have done! In this paper, we introduce a formalization of "what the user intended" in terms of latent concepts implicit to the data generating process that the model was trained on. This formalization allows us to identify some fundamental limitations of prompting. We then use the formalism to develop concept algebra to overcome these limitations. Concept algebra is a way of directly manipulating the concepts expressed in the output through algebraic operations on a suitably defined representation of input prompts. We give examples using concept algebra to overcome limitations of prompting, including concept transfer through arithmetic, and concept nullification through projection. Code available at https://github.com/zihao12/concept-algebra.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge