Simplistic Collection and Labeling Practices Limit the Utility of Benchmark Datasets for Twitter Bot Detection

Accurate bot detection is necessary for the safety and integrity of online platforms. It is also crucial for research on the influence of bots in elections, the spread of misinformation, and financial market manipulation. Platforms deploy infrastructure to flag or remove automated accounts, but their tools and data are not publicly available. Thus, the public must rely on third-party bot detection. These tools employ machine learning and often achieve near perfect performance for classification on existing datasets, suggesting bot detection is accurate, reliable and fit for use in downstream applications. We provide evidence that this is not the case and show that high performance is attributable to limitations in dataset collection and labeling rather than sophistication of the tools. Specifically, we show that simple decision rules -- shallow decision trees trained on a small number of features -- achieve near-state-of-the-art performance on most available datasets and that bot detection datasets, even when combined together, do not generalize well to out-of-sample datasets. Our findings reveal that predictions are highly dependent on each dataset's collection and labeling procedures rather than fundamental differences between bots and humans. These results have important implications for both transparency in sampling and labeling procedures and potential biases in research using existing bot detection tools for pre-processing.

Algorithms and Learning for Fair Portfolio Design

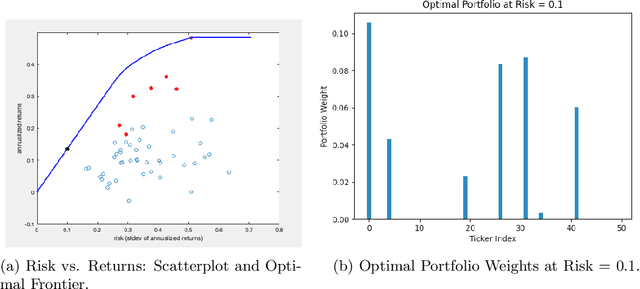
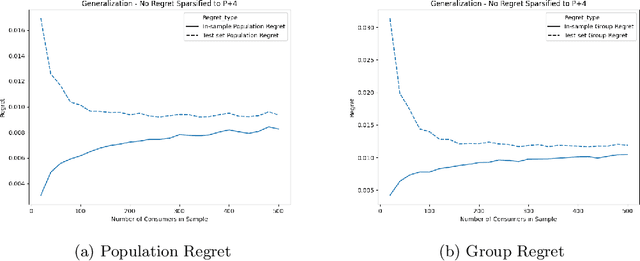
We consider a variation on the classical finance problem of optimal portfolio design. In our setting, a large population of consumers is drawn from some distribution over risk tolerances, and each consumer must be assigned to a portfolio of lower risk than her tolerance. The consumers may also belong to underlying groups (for instance, of demographic properties or wealth), and the goal is to design a small number of portfolios that are fair across groups in a particular and natural technical sense. Our main results are algorithms for optimal and near-optimal portfolio design for both social welfare and fairness objectives, both with and without assumptions on the underlying group structure. We describe an efficient algorithm based on an internal two-player zero-sum game that learns near-optimal fair portfolios ex ante and show experimentally that it can be used to obtain a small set of fair portfolios ex post as well. For the special but natural case in which group structure coincides with risk tolerances (which models the reality that wealthy consumers generally tolerate greater risk), we give an efficient and optimal fair algorithm. We also provide generalization guarantees for the underlying risk distribution that has no dependence on the number of portfolios and illustrate the theory with simulation results.

Equilibrium Characterization for Data Acquisition Games

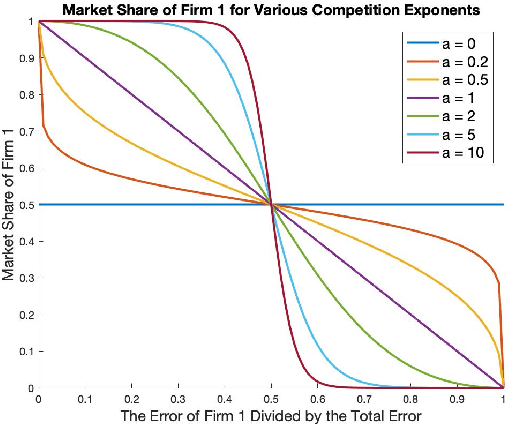
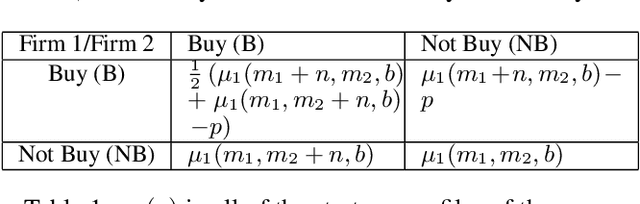
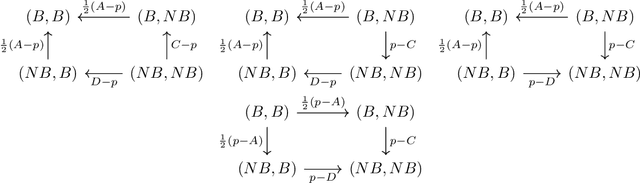
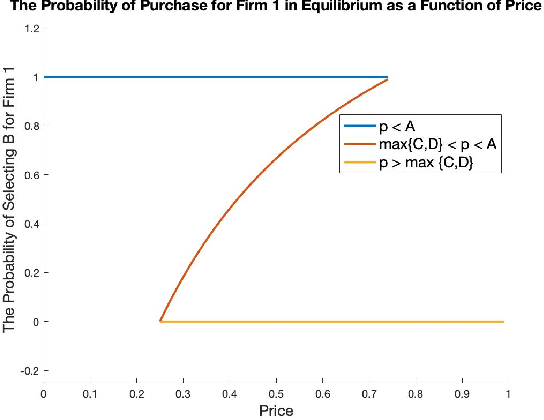
We study a game between two firms in which each provide a service based on machine learning. The firms are presented with the opportunity to purchase a new corpus of data, which will allow them to potentially improve the quality of their products. The firms can decide whether or not they want to buy the data, as well as which learning model to build with that data. We demonstrate a reduction from this potentially complicated action space to a one-shot, two-action game in which each firm only decides whether or not to buy the data. The game admits several regimes which depend on the relative strength of the two firms at the outset and the price at which the data is being offered. We analyze the game's Nash equilibria in all parameter regimes and demonstrate that, in expectation, the outcome of the game is that the initially stronger firm's market position weakens whereas the initially weaker firm's market position becomes stronger. Finally, we consider the perspective of the users of the service and demonstrate that the expected outcome at equilibrium is not the one which maximizes the welfare of the consumers.

Fair Algorithms for Learning in Allocation Problems

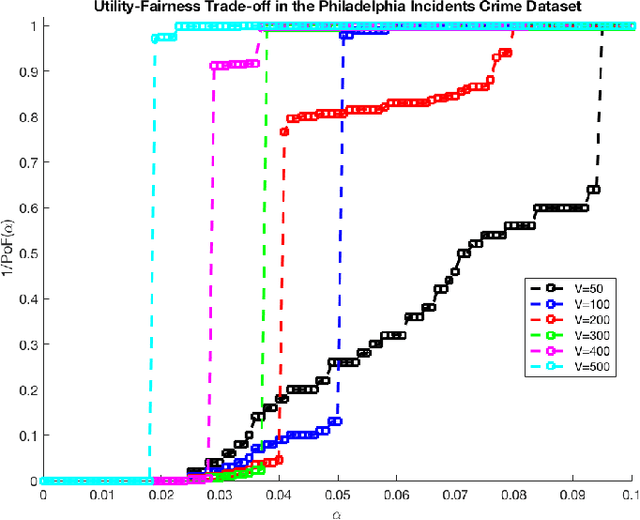
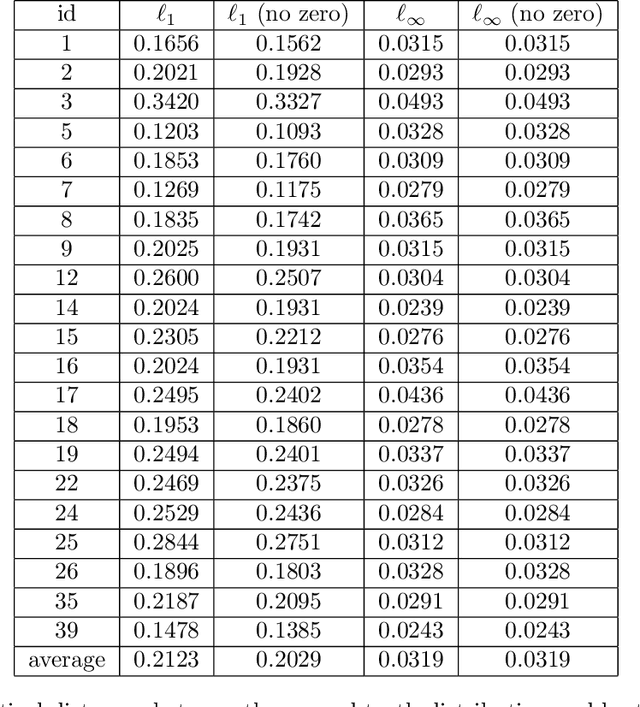
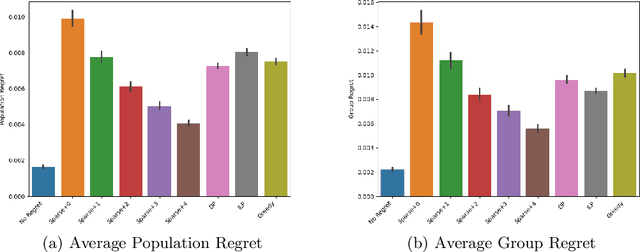
Settings such as lending and policing can be modeled by a centralized agent allocating a resource (loans or police officers) amongst several groups, in order to maximize some objective (loans given that are repaid or criminals that are apprehended). Often in such problems fairness is also a concern. A natural notion of fairness, based on general principles of equality of opportunity, asks that conditional on an individual being a candidate for the resource, the probability of actually receiving it is approximately independent of the individual's group. In lending this means that equally creditworthy individuals in different racial groups have roughly equal chances of receiving a loan. In policing it means that two individuals committing the same crime in different districts would have roughly equal chances of being arrested. We formalize this fairness notion for allocation problems and investigate its algorithmic consequences. Our main technical results include an efficient learning algorithm that converges to an optimal fair allocation even when the frequency of candidates (creditworthy individuals or criminals) in each group is unknown. The algorithm operates in a censored feedback model in which only the number of candidates who received the resource in a given allocation can be observed, rather than the true number of candidates. This models the fact that we do not learn the creditworthiness of individuals we do not give loans to nor learn about crimes committed if the police presence in a district is low. As an application of our framework, we consider the predictive policing problem. The learning algorithm is trained on arrest data gathered from its own deployments on previous days, resulting in a potential feedback loop that our algorithm provably overcomes. We empirically investigate the performance of our algorithm on the Philadelphia Crime Incidents dataset.

Strategic Classification from Revealed Preferences

We study an online linear classification problem, in which the data is generated by strategic agents who manipulate their features in an effort to change the classification outcome. In rounds, the learner deploys a classifier, and an adversarially chosen agent arrives, possibly manipulating her features to optimally respond to the learner. The learner has no knowledge of the agents' utility functions or "real" features, which may vary widely across agents. Instead, the learner is only able to observe their "revealed preferences" --- i.e. the actual manipulated feature vectors they provide. For a broad family of agent cost functions, we give a computationally efficient learning algorithm that is able to obtain diminishing "Stackelberg regret" --- a form of policy regret that guarantees that the learner is obtaining loss nearly as small as that of the best classifier in hindsight, even allowing for the fact that agents will best-respond differently to the optimal classifier.