Adapting to Linear Separable Subsets with Large-Margin in Differentially Private Learning

This paper studies the problem of differentially private empirical risk minimization (DP-ERM) for binary linear classification. We obtain an efficient $(\varepsilon,\delta)$-DP algorithm with an empirical zero-one risk bound of $\tilde{O}\left(\frac{1}{\gamma^2\varepsilon n} + \frac{|S_{\mathrm{out}}|}{\gamma n}\right)$ where $n$ is the number of data points, $S_{\mathrm{out}}$ is an arbitrary subset of data one can remove and $\gamma$ is the margin of linear separation of the remaining data points (after $S_{\mathrm{out}}$ is removed). Here, $\tilde{O}(\cdot)$ hides only logarithmic terms. In the agnostic case, we improve the existing results when the number of outliers is small. Our algorithm is highly adaptive because it does not require knowing the margin parameter $\gamma$ or outlier subset $S_{\mathrm{out}}$. We also derive a utility bound for the advanced private hyperparameter tuning algorithm.

Training People to Reward Robots

Learning from demonstration (LfD) is a technique that allows expert teachers to teach task-oriented skills to robotic systems. However, the most effective way of guiding novice teachers to approach expert-level demonstrations quantitatively for specific teaching tasks remains an open question. To this end, this paper investigates the use of machine teaching (MT) to guide novice teachers to improve their teaching skills based on reinforcement learning from demonstration (RLfD). The paper reports an experiment in which novices receive MT-derived guidance to train their ability to teach a given motor skill with only 8 demonstrations and generalise this to previously unseen ones. Results indicate that the MT-guidance not only enhances robot learning performance by 89% on the training skill but also causes a 70% improvement in robot learning performance on skills not seen by subjects during training. These findings highlight the effectiveness of MT-guidance in upskilling human teaching behaviours, ultimately improving demonstration quality in RLfD.

LEDD: Large Language Model-Empowered Data Discovery in Data Lakes

Data discovery in data lakes with ever increasing datasets has long been recognized as a big challenge in the realm of data management, especially for semantic search of and hierarchical global catalog generation of tables. While large language models (LLMs) facilitate the processing of data semantics, challenges remain in architecting an end-to-end system that comprehensively exploits LLMs for the two semantics-related tasks. In this demo, we propose LEDD, an end-to-end system with an extensible architecture that leverages LLMs to provide hierarchical global catalogs with semantic meanings and semantic table search for data lakes. Specifically, LEDD can return semantically related tables based on natural-language specification. These features make LEDD an ideal foundation for downstream tasks such as model training and schema linking for text-to-SQL tasks. LEDD also provides a simple Python interface to facilitate the extension and the replacement of data discovery algorithms.

Neural Collapse Meets Differential Privacy: Curious Behaviors of NoisyGD with Near-perfect Representation Learning

A recent study by De et al. (2022) has reported that large-scale representation learning through pre-training on a public dataset significantly enhances differentially private (DP) learning in downstream tasks, despite the high dimensionality of the feature space. To theoretically explain this phenomenon, we consider the setting of a layer-peeled model in representation learning, which results in interesting phenomena related to learned features in deep learning and transfer learning, known as Neural Collapse (NC). Within the framework of NC, we establish an error bound indicating that the misclassification error is independent of dimension when the distance between actual features and the ideal ones is smaller than a threshold. Additionally, the quality of the features in the last layer is empirically evaluated under different pre-trained models within the framework of NC, showing that a more powerful transformer leads to a better feature representation. Furthermore, we reveal that DP fine-tuning is less robust compared to fine-tuning without DP, particularly in the presence of perturbations. These observations are supported by both theoretical analyses and experimental evaluation. Moreover, to enhance the robustness of DP fine-tuning, we suggest several strategies, such as feature normalization or employing dimension reduction methods like Principal Component Analysis (PCA). Empirically, we demonstrate a significant improvement in testing accuracy by conducting PCA on the last-layer features.

Sub-Adjacent Transformer: Improving Time Series Anomaly Detection with Reconstruction Error from Sub-Adjacent Neighborhoods

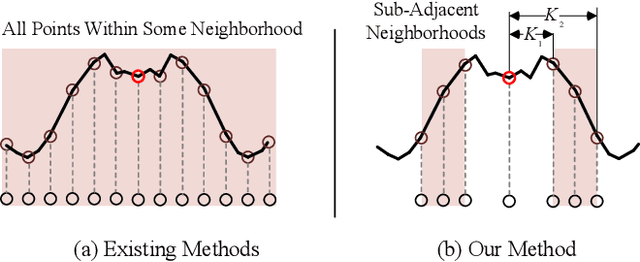
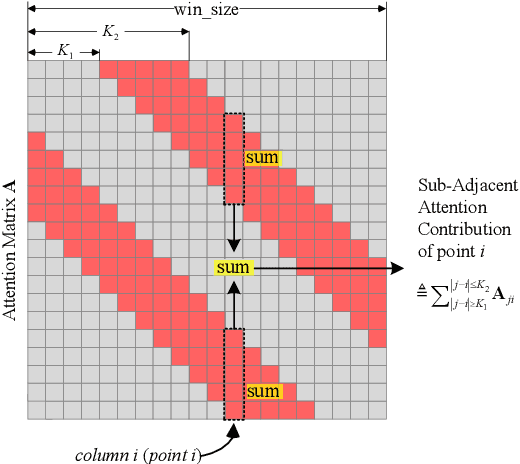
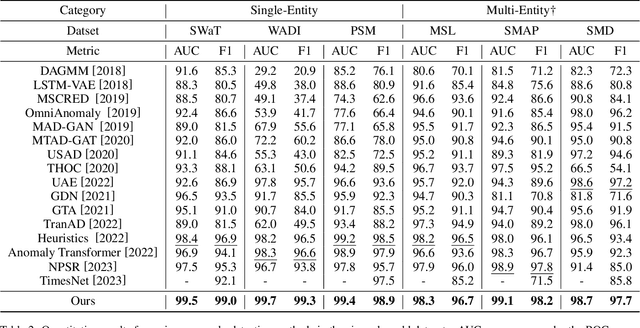
In this paper, we present the Sub-Adjacent Transformer with a novel attention mechanism for unsupervised time series anomaly detection. Unlike previous approaches that rely on all the points within some neighborhood for time point reconstruction, our method restricts the attention to regions not immediately adjacent to the target points, termed sub-adjacent neighborhoods. Our key observation is that owing to the rarity of anomalies, they typically exhibit more pronounced differences from their sub-adjacent neighborhoods than from their immediate vicinities. By focusing the attention on the sub-adjacent areas, we make the reconstruction of anomalies more challenging, thereby enhancing their detectability. Technically, our approach concentrates attention on the non-diagonal areas of the attention matrix by enlarging the corresponding elements in the training stage. To facilitate the implementation of the desired attention matrix pattern, we adopt linear attention because of its flexibility and adaptability. Moreover, a learnable mapping function is proposed to improve the performance of linear attention. Empirically, the Sub-Adjacent Transformer achieves state-of-the-art performance across six real-world anomaly detection benchmarks, covering diverse fields such as server monitoring, space exploration, and water treatment.

Threshold KNN-Shapley: A Linear-Time and Privacy-Friendly Approach to Data Valuation

Data valuation, a critical aspect of data-centric ML research, aims to quantify the usefulness of individual data sources in training machine learning (ML) models. However, data valuation faces significant yet frequently overlooked privacy challenges despite its importance. This paper studies these challenges with a focus on KNN-Shapley, one of the most practical data valuation methods nowadays. We first emphasize the inherent privacy risks of KNN-Shapley, and demonstrate the significant technical difficulties in adapting KNN-Shapley to accommodate differential privacy (DP). To overcome these challenges, we introduce TKNN-Shapley, a refined variant of KNN-Shapley that is privacy-friendly, allowing for straightforward modifications to incorporate DP guarantee (DP-TKNN-Shapley). We show that DP-TKNN-Shapley has several advantages and offers a superior privacy-utility tradeoff compared to naively privatized KNN-Shapley in discerning data quality. Moreover, even non-private TKNN-Shapley achieves comparable performance as KNN-Shapley. Overall, our findings suggest that TKNN-Shapley is a promising alternative to KNN-Shapley, particularly for real-world applications involving sensitive data.

"Private Prediction Strikes Back!'' Private Kernelized Nearest Neighbors with Individual Renyi Filter

Most existing approaches of differentially private (DP) machine learning focus on private training. Despite its many advantages, private training lacks the flexibility in adapting to incremental changes to the training dataset such as deletion requests from exercising GDPR's right to be forgotten. We revisit a long-forgotten alternative, known as private prediction, and propose a new algorithm named Individual Kernelized Nearest Neighbor (Ind-KNN). Ind-KNN is easily updatable over dataset changes and it allows precise control of the R\'{e}nyi DP at an individual user level -- a user's privacy loss is measured by the exact amount of her contribution to predictions; and a user is removed if her prescribed privacy budget runs out. Our results show that Ind-KNN consistently improves the accuracy over existing private prediction methods for a wide range of $\epsilon$ on four vision and language tasks. We also illustrate several cases under which Ind-KNN is preferable over private training with NoisySGD.

Generalized PTR: User-Friendly Recipes for Data-Adaptive Algorithms with Differential Privacy

The ''Propose-Test-Release'' (PTR) framework is a classic recipe for designing differentially private (DP) algorithms that are data-adaptive, i.e. those that add less noise when the input dataset is nice. We extend PTR to a more general setting by privately testing data-dependent privacy losses rather than local sensitivity, hence making it applicable beyond the standard noise-adding mechanisms, e.g. to queries with unbounded or undefined sensitivity. We demonstrate the versatility of generalized PTR using private linear regression as a case study. Additionally, we apply our algorithm to solve an open problem from ''Private Aggregation of Teacher Ensembles (PATE)'' -- privately releasing the entire model with a delicate data-dependent analysis.

Adaptive Private-K-Selection with Adaptive K and Application to Multi-label PATE

We provide an end-to-end Renyi DP based-framework for differentially private top-$k$ selection. Unlike previous approaches, which require a data-independent choice on $k$, we propose to privately release a data-dependent choice of $k$ such that the gap between $k$-th and the $(k+1)$st "quality" is large. This is achieved by a novel application of the Report-Noisy-Max. Not only does this eliminate one hyperparameter, the adaptive choice of $k$ also certifies the stability of the top-$k$ indices in the unordered set so we can release them using a variant of propose-test-release (PTR) without adding noise. We show that our construction improves the privacy-utility trade-offs compared to the previous top-$k$ selection algorithms theoretically and empirically. Additionally, we apply our algorithm to "Private Aggregation of Teacher Ensembles (PATE)" in multi-label classification tasks with a large number of labels and show that it leads to significant performance gains.

Optimal Accounting of Differential Privacy via Characteristic Function

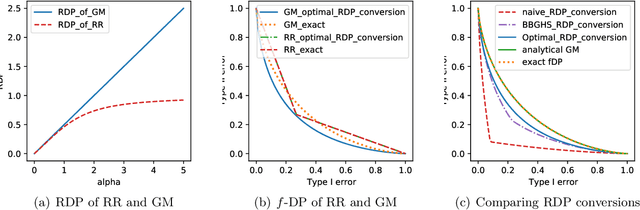
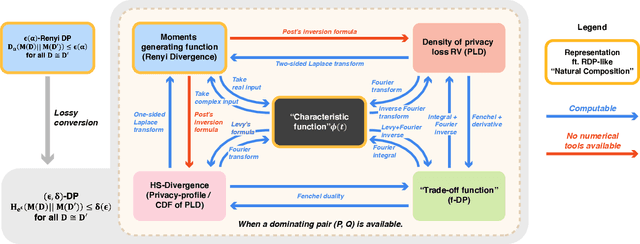
Characterizing the privacy degradation over compositions, i.e., privacy accounting, is a fundamental topic in differential privacy (DP) with many applications to differentially private machine learning and federated learning. We propose a unification of recent advances (Renyi DP, privacy profiles, $f$-DP and the PLD formalism) via the characteristic function ($\phi$-function) of a certain ``worst-case'' privacy loss random variable. We show that our approach allows natural adaptive composition like Renyi DP, provides exactly tight privacy accounting like PLD, and can be (often losslessly) converted to privacy profile and $f$-DP, thus providing $(\epsilon,\delta)$-DP guarantees and interpretable tradeoff functions. Algorithmically, we propose an analytical Fourier accountant that represents the complex logarithm of $\phi$-functions symbolically and uses Gaussian quadrature for numerical computation. On several popular DP mechanisms and their subsampled counterparts, we demonstrate the flexibility and tightness of our approach in theory and experiments.