BiasConnect: Investigating Bias Interactions in Text-to-Image Models

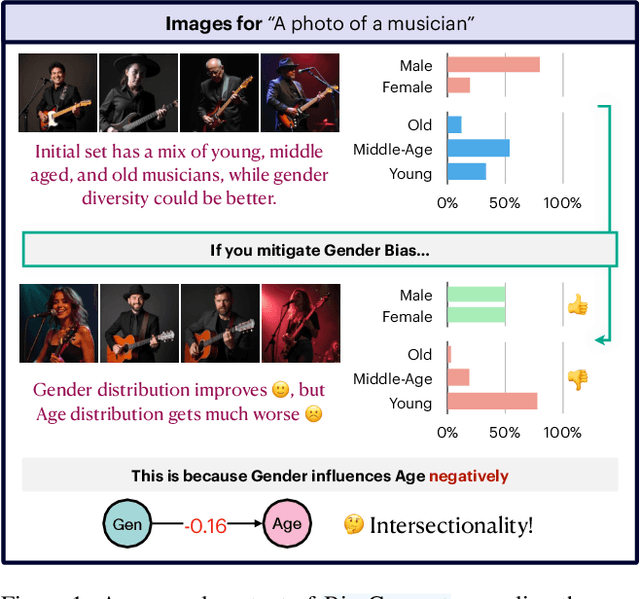
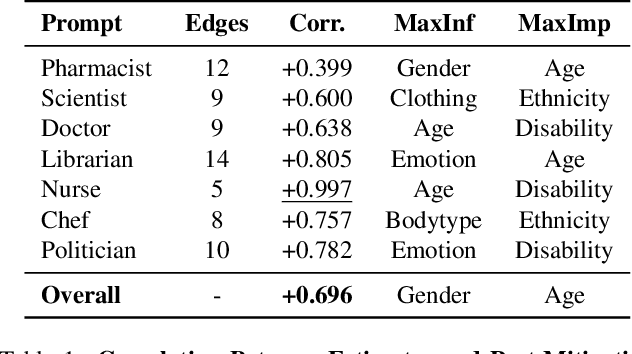
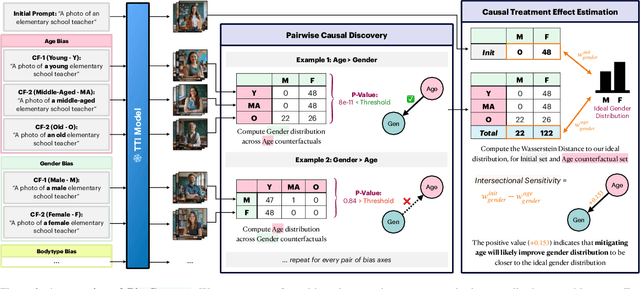
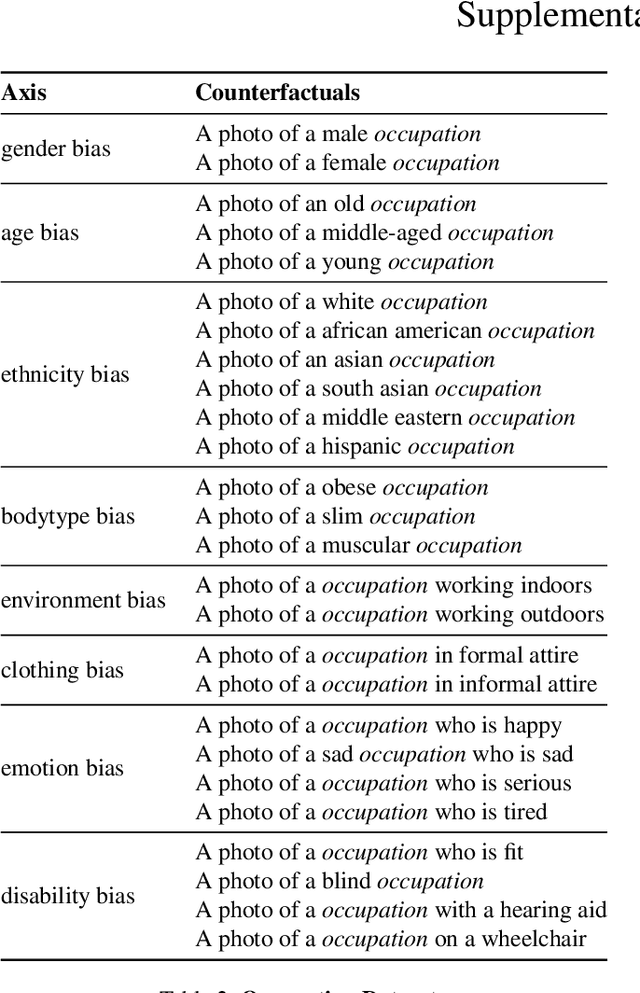
The biases exhibited by Text-to-Image (TTI) models are often treated as if they are independent, but in reality, they may be deeply interrelated. Addressing bias along one dimension, such as ethnicity or age, can inadvertently influence another dimension, like gender, either mitigating or exacerbating existing disparities. Understanding these interdependencies is crucial for designing fairer generative models, yet measuring such effects quantitatively remains a challenge. In this paper, we aim to address these questions by introducing BiasConnect, a novel tool designed to analyze and quantify bias interactions in TTI models. Our approach leverages a counterfactual-based framework to generate pairwise causal graphs that reveals the underlying structure of bias interactions for the given text prompt. Additionally, our method provides empirical estimates that indicate how other bias dimensions shift toward or away from an ideal distribution when a given bias is modified. Our estimates have a strong correlation (+0.69) with the interdependency observations post bias mitigation. We demonstrate the utility of BiasConnect for selecting optimal bias mitigation axes, comparing different TTI models on the dependencies they learn, and understanding the amplification of intersectional societal biases in TTI models.

Reconciling Individual Probability Forecasts

Individual probabilities refer to the probabilities of outcomes that are realized only once: the probability that it will rain tomorrow, the probability that Alice will die within the next 12 months, the probability that Bob will be arrested for a violent crime in the next 18 months, etc. Individual probabilities are fundamentally unknowable. Nevertheless, we show that two parties who agree on the data -- or on how to sample from a data distribution -- cannot agree to disagree on how to model individual probabilities. This is because any two models of individual probabilities that substantially disagree can together be used to empirically falsify and improve at least one of the two models. This can be efficiently iterated in a process of "reconciliation" that results in models that both parties agree are superior to the models they started with, and which themselves (almost) agree on the forecasts of individual probabilities (almost) everywhere. We conclude that although individual probabilities are unknowable, they are contestable via a computationally and data efficient process that must lead to agreement. Thus we cannot find ourselves in a situation in which we have two equally accurate and unimprovable models that disagree substantially in their predictions -- providing an answer to what is sometimes called the predictive or model multiplicity problem.