Ali Vakilian
Guessing Efficiently for Constrained Subspace Approximation
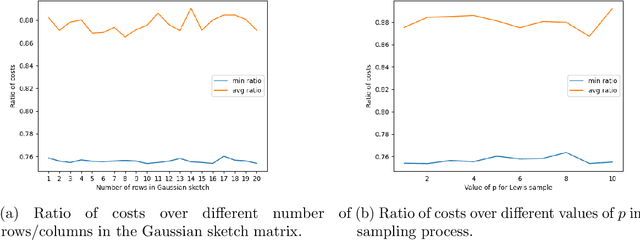
Apr 29, 2025Abstract:In this paper we study constrained subspace approximation problem. Given a set of $n$ points $\{a_1,\ldots,a_n\}$ in $\mathbb{R}^d$, the goal of the {\em subspace approximation} problem is to find a $k$ dimensional subspace that best approximates the input points. More precisely, for a given $p\geq 1$, we aim to minimize the $p$th power of the $\ell_p$ norm of the error vector $(\|a_1-\bm{P}a_1\|,\ldots,\|a_n-\bm{P}a_n\|)$, where $\bm{P}$ denotes the projection matrix onto the subspace and the norms are Euclidean. In \emph{constrained} subspace approximation (CSA), we additionally have constraints on the projection matrix $\bm{P}$. In its most general form, we require $\bm{P}$ to belong to a given subset $\mathcal{S}$ that is described explicitly or implicitly. We introduce a general framework for constrained subspace approximation. Our approach, that we term coreset-guess-solve, yields either $(1+\varepsilon)$-multiplicative or $\varepsilon$-additive approximations for a variety of constraints. We show that it provides new algorithms for partition-constrained subspace approximation with applications to {\it fair} subspace approximation, $k$-means clustering, and projected non-negative matrix factorization, among others. Specifically, while we reconstruct the best known bounds for $k$-means clustering in Euclidean spaces, we improve the known results for the remainder of the problems.
On Socially Fair Low-Rank Approximation and Column Subset Selection
Dec 08, 2024
Abstract:Low-rank approximation and column subset selection are two fundamental and related problems that are applied across a wealth of machine learning applications. In this paper, we study the question of socially fair low-rank approximation and socially fair column subset selection, where the goal is to minimize the loss over all sub-populations of the data. We show that surprisingly, even constant-factor approximation to fair low-rank approximation requires exponential time under certain standard complexity hypotheses. On the positive side, we give an algorithm for fair low-rank approximation that, for a constant number of groups and constant-factor accuracy, runs in $2^{\text{poly}(k)}$ time rather than the na\"{i}ve $n^{\text{poly}(k)}$, which is a substantial improvement when the dataset has a large number $n$ of observations. We then show that there exist bicriteria approximation algorithms for fair low-rank approximation and fair column subset selection that run in polynomial time.
Minimax Group Fairness in Strategic Classification
Oct 03, 2024Abstract:In strategic classification, agents manipulate their features, at a cost, to receive a positive classification outcome from the learner's classifier. The goal of the learner in such settings is to learn a classifier that is robust to strategic manipulations. While the majority of works in this domain consider accuracy as the primary objective of the learner, in this work, we consider learning objectives that have group fairness guarantees in addition to accuracy guarantees. We work with the minimax group fairness notion that asks for minimizing the maximal group error rate across population groups. We formalize a fairness-aware Stackelberg game between a population of agents consisting of several groups, with each group having its own cost function, and a learner in the agnostic PAC setting in which the learner is working with a hypothesis class H. When the cost functions of the agents are separable, we show the existence of an efficient algorithm that finds an approximately optimal deterministic classifier for the learner when the number of groups is small. This algorithm remains efficient, both statistically and computationally, even when H is the set of all classifiers. We then consider cost functions that are not necessarily separable and show the existence of oracle-efficient algorithms that find approximately optimal randomized classifiers for the learner when H has finite strategic VC dimension. These algorithms work under the assumption that the learner is fully transparent: the learner draws a classifier from its distribution (randomized classifier) before the agents respond by manipulating their feature vectors. We highlight the effectiveness of such transparency in developing oracle-efficient algorithms. We conclude with verifying the efficacy of our algorithms on real data by conducting an experimental analysis.
A Polynomial-Time Approximation for Pairwise Fair $k$-Median Clustering
May 16, 2024
Abstract:In this work, we study pairwise fair clustering with $\ell \ge 2$ groups, where for every cluster $C$ and every group $i \in [\ell]$, the number of points in $C$ from group $i$ must be at most $t$ times the number of points in $C$ from any other group $j \in [\ell]$, for a given integer $t$. To the best of our knowledge, only bi-criteria approximation and exponential-time algorithms follow for this problem from the prior work on fair clustering problems when $\ell > 2$. In our work, focusing on the $\ell > 2$ case, we design the first polynomial-time $(t^{\ell}\cdot \ell\cdot k)^{O(\ell)}$-approximation for this problem with $k$-median cost that does not violate the fairness constraints. We complement our algorithmic result by providing hardness of approximation results, which show that our problem even when $\ell=2$ is almost as hard as the popular uniform capacitated $k$-median, for which no polynomial-time algorithm with an approximation factor of $o(\log k)$ is known.
Scalable Algorithms for Individual Preference Stable Clustering
Mar 15, 2024Abstract:In this paper, we study the individual preference (IP) stability, which is an notion capturing individual fairness and stability in clustering. Within this setting, a clustering is $\alpha$-IP stable when each data point's average distance to its cluster is no more than $\alpha$ times its average distance to any other cluster. In this paper, we study the natural local search algorithm for IP stable clustering. Our analysis confirms a $O(\log n)$-IP stability guarantee for this algorithm, where $n$ denotes the number of points in the input. Furthermore, by refining the local search approach, we show it runs in an almost linear time, $\tilde{O}(nk)$.
Learning-Based Algorithms for Graph Searching Problems
Feb 27, 2024
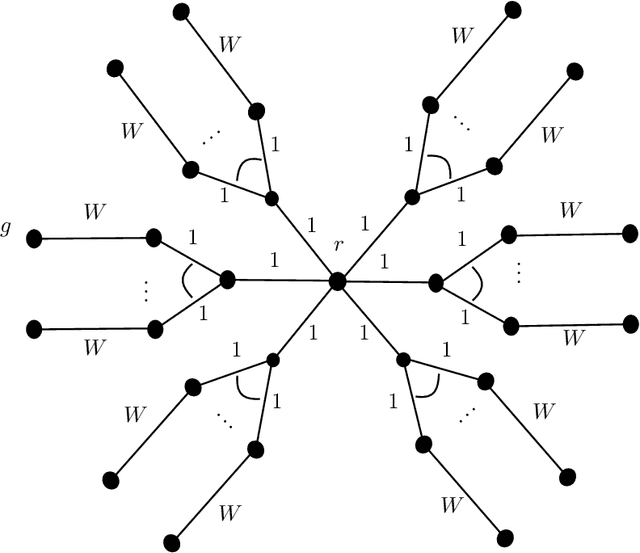
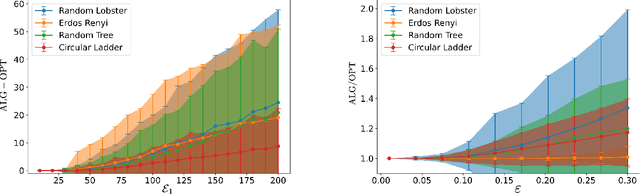

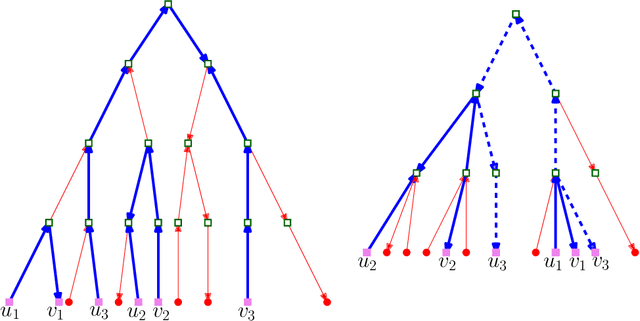
Abstract:We consider the problem of graph searching with prediction recently introduced by Banerjee et al. (2022). In this problem, an agent, starting at some vertex $r$ has to traverse a (potentially unknown) graph $G$ to find a hidden goal node $g$ while minimizing the total distance travelled. We study a setting in which at any node $v$, the agent receives a noisy estimate of the distance from $v$ to $g$. We design algorithms for this search task on unknown graphs. We establish the first formal guarantees on unknown weighted graphs and provide lower bounds showing that the algorithms we propose have optimal or nearly-optimal dependence on the prediction error. Further, we perform numerical experiments demonstrating that in addition to being robust to adversarial error, our algorithms perform well in typical instances in which the error is stochastic. Finally, we provide alternative simpler performance bounds on the algorithms of Banerjee et al. (2022) for the case of searching on a known graph, and establish new lower bounds for this setting.
Bayesian Strategic Classification
Feb 13, 2024Abstract:In strategic classification, agents modify their features, at a cost, to ideally obtain a positive classification from the learner's classifier. The typical response of the learner is to carefully modify their classifier to be robust to such strategic behavior. When reasoning about agent manipulations, most papers that study strategic classification rely on the following strong assumption: agents fully know the exact parameters of the deployed classifier by the learner. This often is an unrealistic assumption when using complex or proprietary machine learning techniques in real-world prediction tasks. We initiate the study of partial information release by the learner in strategic classification. We move away from the traditional assumption that agents have full knowledge of the classifier. Instead, we consider agents that have a common distributional prior on which classifier the learner is using. The learner in our model can reveal truthful, yet not necessarily complete, information about the deployed classifier to the agents. The learner's goal is to release just enough information about the classifier to maximize accuracy. We show how such partial information release can, counter-intuitively, benefit the learner's accuracy, despite increasing agents' abilities to manipulate. We show that while it is intractable to compute the best response of an agent in the general case, there exist oracle-efficient algorithms that can solve the best response of the agents when the learner's hypothesis class is the class of linear classifiers, or when the agents' cost function satisfies a natural notion of submodularity as we define. We then turn our attention to the learner's optimization problem and provide both positive and negative results on the algorithmic problem of how much information the learner should release about the classifier to maximize their expected accuracy.
Improved Frequency Estimation Algorithms with and without Predictions
Dec 12, 2023



Abstract:Estimating frequencies of elements appearing in a data stream is a key task in large-scale data analysis. Popular sketching approaches to this problem (e.g., CountMin and CountSketch) come with worst-case guarantees that probabilistically bound the error of the estimated frequencies for any possible input. The work of Hsu et al. (2019) introduced the idea of using machine learning to tailor sketching algorithms to the specific data distribution they are being run on. In particular, their learning-augmented frequency estimation algorithm uses a learned heavy-hitter oracle which predicts which elements will appear many times in the stream. We give a novel algorithm, which in some parameter regimes, already theoretically outperforms the learning based algorithm of Hsu et al. without the use of any predictions. Augmenting our algorithm with heavy-hitter predictions further reduces the error and improves upon the state of the art. Empirically, our algorithms achieve superior performance in all experiments compared to prior approaches.
Tight Bounds for Volumetric Spanners and Applications
Sep 29, 2023
Abstract:Given a set of points of interest, a volumetric spanner is a subset of the points using which all the points can be expressed using "small" coefficients (measured in an appropriate norm). Formally, given a set of vectors $X = \{v_1, v_2, \dots, v_n\}$, the goal is to find $T \subseteq [n]$ such that every $v \in X$ can be expressed as $\sum_{i\in T} \alpha_i v_i$, with $\|\alpha\|$ being small. This notion, which has also been referred to as a well-conditioned basis, has found several applications, including bandit linear optimization, determinant maximization, and matrix low rank approximation. In this paper, we give almost optimal bounds on the size of volumetric spanners for all $\ell_p$ norms, and show that they can be constructed using a simple local search procedure. We then show the applications of our result to other tasks and in particular the problem of finding coresets for the Minimum Volume Enclosing Ellipsoid (MVEE) problem.
Constant Approximation for Individual Preference Stable Clustering
Sep 28, 2023



Abstract:Individual preference (IP) stability, introduced by Ahmadi et al. (ICML 2022), is a natural clustering objective inspired by stability and fairness constraints. A clustering is $\alpha$-IP stable if the average distance of every data point to its own cluster is at most $\alpha$ times the average distance to any other cluster. Unfortunately, determining if a dataset admits a $1$-IP stable clustering is NP-Hard. Moreover, before this work, it was unknown if an $o(n)$-IP stable clustering always \emph{exists}, as the prior state of the art only guaranteed an $O(n)$-IP stable clustering. We close this gap in understanding and show that an $O(1)$-IP stable clustering always exists for general metrics, and we give an efficient algorithm which outputs such a clustering. We also introduce generalizations of IP stability beyond average distance and give efficient, near-optimal algorithms in the cases where we consider the maximum and minimum distances within and between clusters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge