Pattara Sukprasert
Constant Approximation for Individual Preference Stable Clustering
Sep 28, 2023



Abstract:Individual preference (IP) stability, introduced by Ahmadi et al. (ICML 2022), is a natural clustering objective inspired by stability and fairness constraints. A clustering is $\alpha$-IP stable if the average distance of every data point to its own cluster is at most $\alpha$ times the average distance to any other cluster. Unfortunately, determining if a dataset admits a $1$-IP stable clustering is NP-Hard. Moreover, before this work, it was unknown if an $o(n)$-IP stable clustering always \emph{exists}, as the prior state of the art only guaranteed an $O(n)$-IP stable clustering. We close this gap in understanding and show that an $O(1)$-IP stable clustering always exists for general metrics, and we give an efficient algorithm which outputs such a clustering. We also introduce generalizations of IP stability beyond average distance and give efficient, near-optimal algorithms in the cases where we consider the maximum and minimum distances within and between clusters.
Individual Preference Stability for Clustering
Jul 07, 2022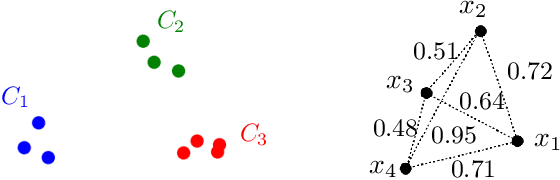
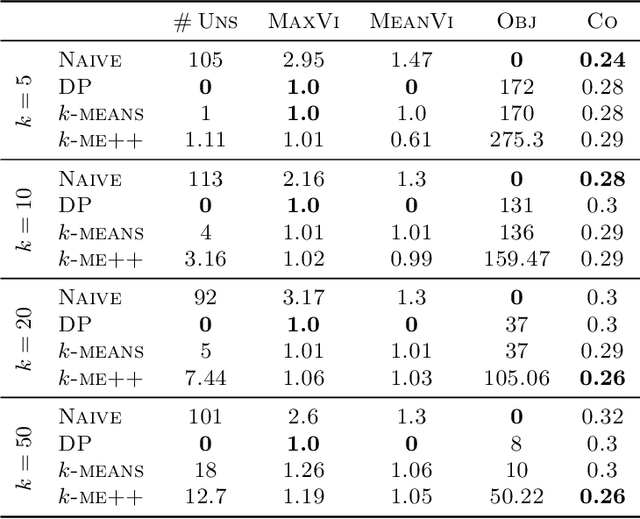
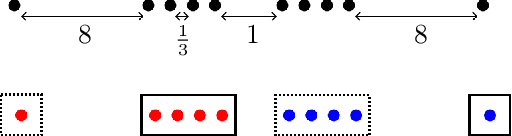
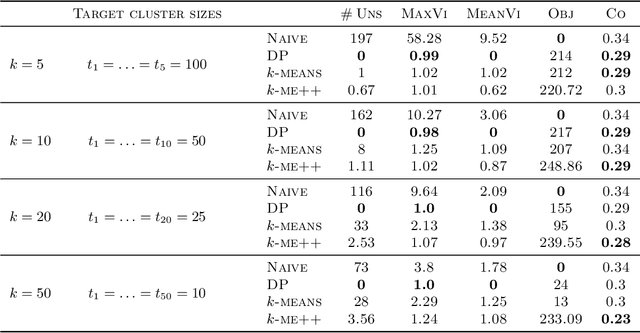
Abstract:In this paper, we propose a natural notion of individual preference (IP) stability for clustering, which asks that every data point, on average, is closer to the points in its own cluster than to the points in any other cluster. Our notion can be motivated from several perspectives, including game theory and algorithmic fairness. We study several questions related to our proposed notion. We first show that deciding whether a given data set allows for an IP-stable clustering in general is NP-hard. As a result, we explore the design of efficient algorithms for finding IP-stable clusterings in some restricted metric spaces. We present a polytime algorithm to find a clustering satisfying exact IP-stability on the real line, and an efficient algorithm to find an IP-stable 2-clustering for a tree metric. We also consider relaxing the stability constraint, i.e., every data point should not be too far from its own cluster compared to any other cluster. For this case, we provide polytime algorithms with different guarantees. We evaluate some of our algorithms and several standard clustering approaches on real data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge