Learning-Augmented Frequent Directions

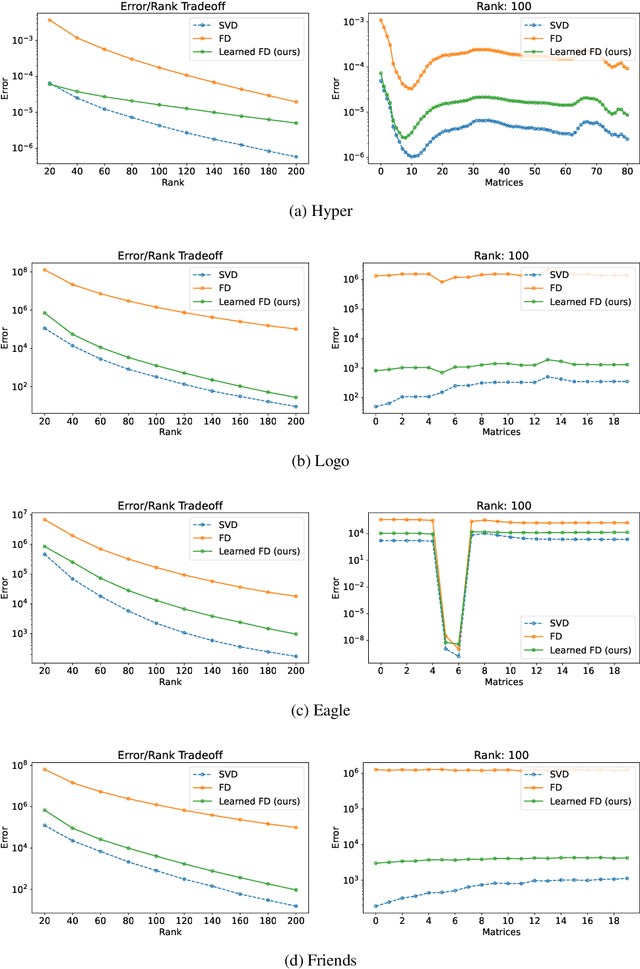
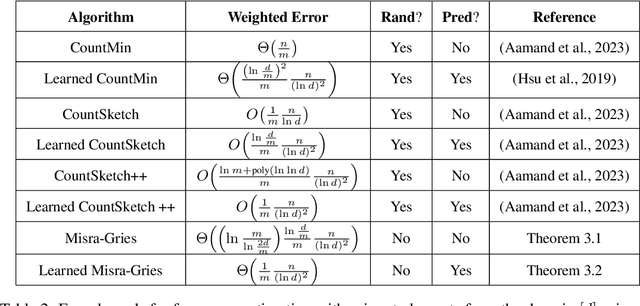
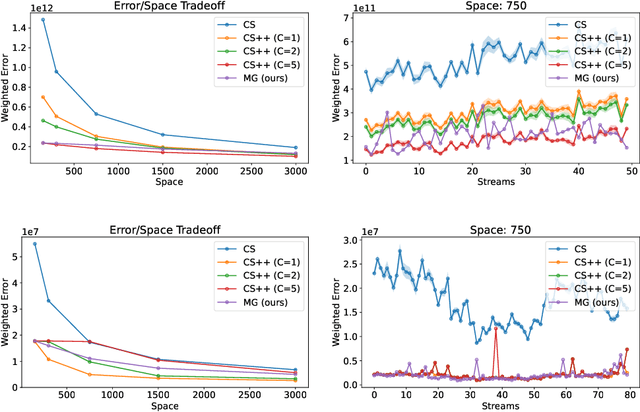
An influential paper of Hsu et al. (ICLR'19) introduced the study of learning-augmented streaming algorithms in the context of frequency estimation. A fundamental problem in the streaming literature, the goal of frequency estimation is to approximate the number of occurrences of items appearing in a long stream of data using only a small amount of memory. Hsu et al. develop a natural framework to combine the worst-case guarantees of popular solutions such as CountMin and CountSketch with learned predictions of high frequency elements. They demonstrate that learning the underlying structure of data can be used to yield better streaming algorithms, both in theory and practice. We simplify and generalize past work on learning-augmented frequency estimation. Our first contribution is a learning-augmented variant of the Misra-Gries algorithm which improves upon the error of learned CountMin and learned CountSketch and achieves the state-of-the-art performance of randomized algorithms (Aamand et al., NeurIPS'23) with a simpler, deterministic algorithm. Our second contribution is to adapt learning-augmentation to a high-dimensional generalization of frequency estimation corresponding to finding important directions (top singular vectors) of a matrix given its rows one-by-one in a stream. We analyze a learning-augmented variant of the Frequent Directions algorithm, extending the theoretical and empirical understanding of learned predictions to matrix streaming.

Private Text Generation by Seeding Large Language Model Prompts

We explore how private synthetic text can be generated by suitably prompting a large language model (LLM). This addresses a challenge for organizations like hospitals, which hold sensitive text data like patient medical records, and wish to share it in order to train machine learning models for medical tasks, while preserving patient privacy. Methods that rely on training or finetuning a model may be out of reach, either due to API limits of third-party LLMs, or due to ethical and legal prohibitions on sharing the private data with the LLM itself. We propose Differentially Private Keyphrase Prompt Seeding (DP-KPS), a method that generates a private synthetic text corpus from a sensitive input corpus, by accessing an LLM only through privatized prompts. It is based on seeding the prompts with private samples from a distribution over phrase embeddings, thus capturing the input corpus while achieving requisite output diversity and maintaining differential privacy. We evaluate DP-KPS on downstream ML text classification tasks, and show that the corpora it generates preserve much of the predictive power of the original ones. Our findings offer hope that institutions can reap ML insights by privately sharing data with simple prompts and little compute.

Statistical-Computational Trade-offs for Density Estimation

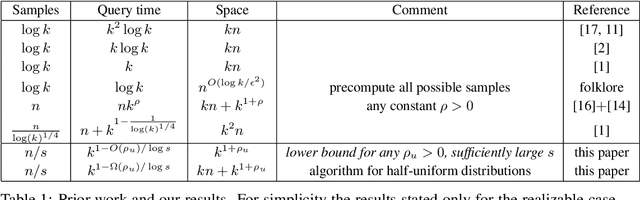
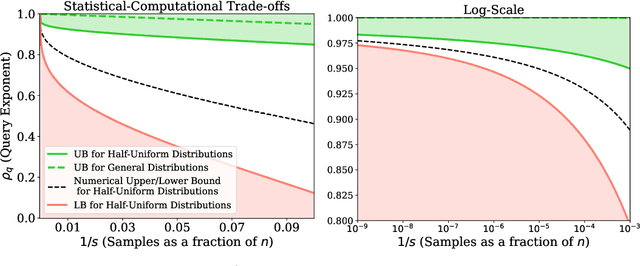
We study the density estimation problem defined as follows: given $k$ distributions $p_1, \ldots, p_k$ over a discrete domain $[n]$, as well as a collection of samples chosen from a ``query'' distribution $q$ over $[n]$, output $p_i$ that is ``close'' to $q$. Recently~\cite{aamand2023data} gave the first and only known result that achieves sublinear bounds in {\em both} the sampling complexity and the query time while preserving polynomial data structure space. However, their improvement over linear samples and time is only by subpolynomial factors. Our main result is a lower bound showing that, for a broad class of data structures, their bounds cannot be significantly improved. In particular, if an algorithm uses $O(n/\log^c k)$ samples for some constant $c>0$ and polynomial space, then the query time of the data structure must be at least $k^{1-O(1)/\log \log k}$, i.e., close to linear in the number of distributions $k$. This is a novel \emph{statistical-computational} trade-off for density estimation, demonstrating that any data structure must use close to a linear number of samples or take close to linear query time. The lower bound holds even in the realizable case where $q=p_i$ for some $i$, and when the distributions are flat (specifically, all distributions are uniform over half of the domain $[n]$). We also give a simple data structure for our lower bound instance with asymptotically matching upper bounds. Experiments show that the data structure is quite efficient in practice.

Evaluating the World Model Implicit in a Generative Model

Recent work suggests that large language models may implicitly learn world models. How should we assess this possibility? We formalize this question for the case where the underlying reality is governed by a deterministic finite automaton. This includes problems as diverse as simple logical reasoning, geographic navigation, game-playing, and chemistry. We propose new evaluation metrics for world model recovery inspired by the classic Myhill-Nerode theorem from language theory. We illustrate their utility in three domains: game playing, logic puzzles, and navigation. In all domains, the generative models we consider do well on existing diagnostics for assessing world models, but our evaluation metrics reveal their world models to be far less coherent than they appear. Such incoherence creates fragility: using a generative model to solve related but subtly different tasks can lead it to fail badly. Building generative models that meaningfully capture the underlying logic of the domains they model would be immensely valuable; our results suggest new ways to assess how close a given model is to that goal.

Improved Frequency Estimation Algorithms with and without Predictions

Estimating frequencies of elements appearing in a data stream is a key task in large-scale data analysis. Popular sketching approaches to this problem (e.g., CountMin and CountSketch) come with worst-case guarantees that probabilistically bound the error of the estimated frequencies for any possible input. The work of Hsu et al. (2019) introduced the idea of using machine learning to tailor sketching algorithms to the specific data distribution they are being run on. In particular, their learning-augmented frequency estimation algorithm uses a learned heavy-hitter oracle which predicts which elements will appear many times in the stream. We give a novel algorithm, which in some parameter regimes, already theoretically outperforms the learning based algorithm of Hsu et al. without the use of any predictions. Augmenting our algorithm with heavy-hitter predictions further reduces the error and improves upon the state of the art. Empirically, our algorithms achieve superior performance in all experiments compared to prior approaches.

Constant Approximation for Individual Preference Stable Clustering

Individual preference (IP) stability, introduced by Ahmadi et al. (ICML 2022), is a natural clustering objective inspired by stability and fairness constraints. A clustering is $\alpha$-IP stable if the average distance of every data point to its own cluster is at most $\alpha$ times the average distance to any other cluster. Unfortunately, determining if a dataset admits a $1$-IP stable clustering is NP-Hard. Moreover, before this work, it was unknown if an $o(n)$-IP stable clustering always \emph{exists}, as the prior state of the art only guaranteed an $O(n)$-IP stable clustering. We close this gap in understanding and show that an $O(1)$-IP stable clustering always exists for general metrics, and we give an efficient algorithm which outputs such a clustering. We also introduce generalizations of IP stability beyond average distance and give efficient, near-optimal algorithms in the cases where we consider the maximum and minimum distances within and between clusters.

Data Structures for Density Estimation

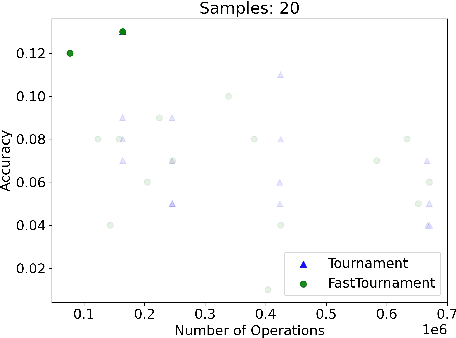
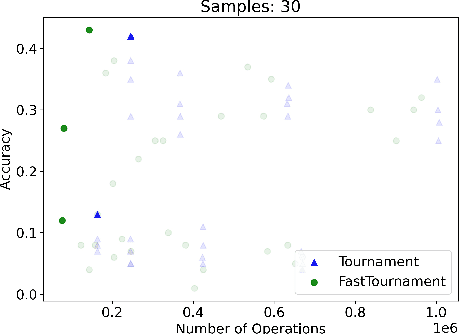
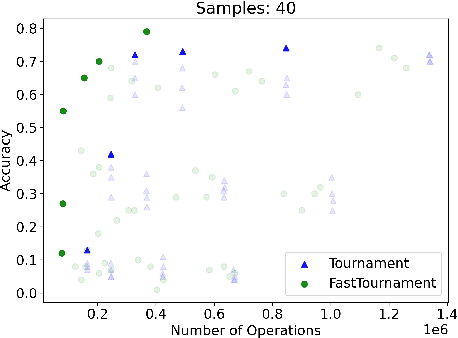
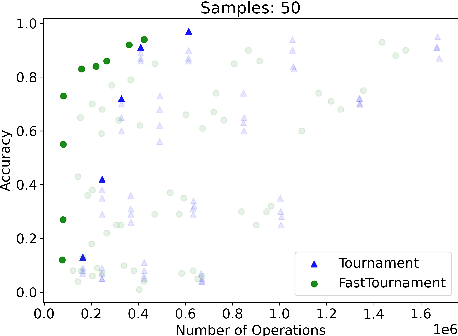
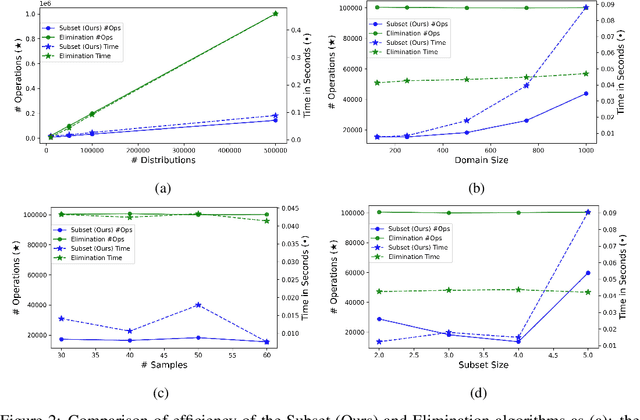
We study statistical/computational tradeoffs for the following density estimation problem: given $k$ distributions $v_1, \ldots, v_k$ over a discrete domain of size $n$, and sampling access to a distribution $p$, identify $v_i$ that is "close" to $p$. Our main result is the first data structure that, given a sublinear (in $n$) number of samples from $p$, identifies $v_i$ in time sublinear in $k$. We also give an improved version of the algorithm of Acharya et al. (2018) that reports $v_i$ in time linear in $k$. The experimental evaluation of the latter algorithm shows that it achieves a significant reduction in the number of operations needed to achieve a given accuracy compared to prior work.

Learned Interpolation for Better Streaming Quantile Approximation with Worst-Case Guarantees

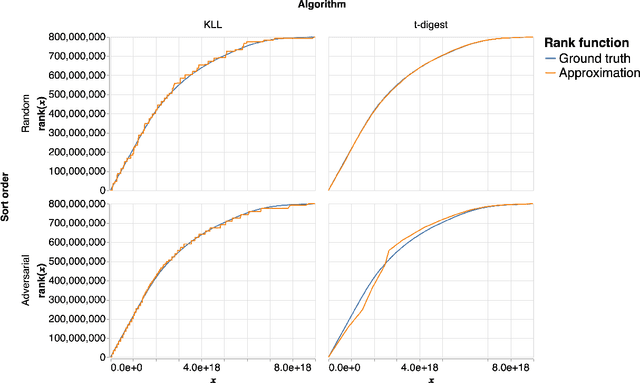
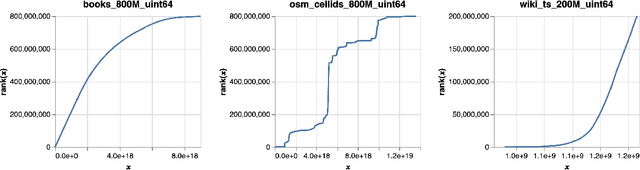
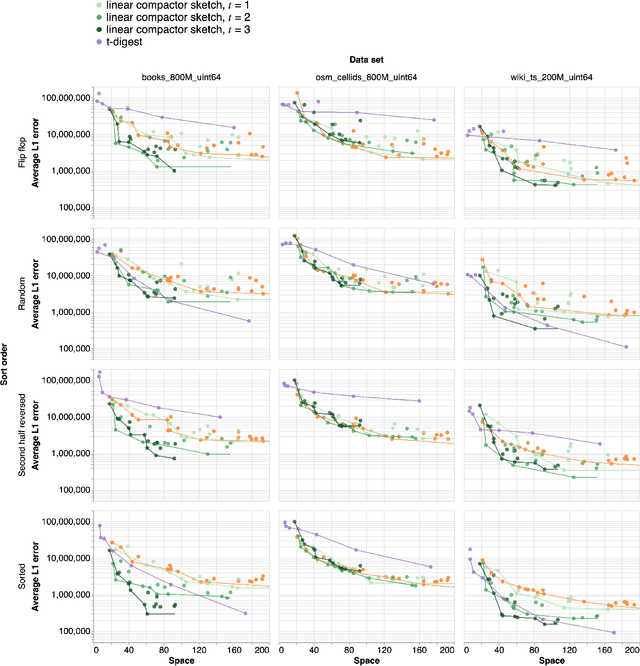
An $\varepsilon$-approximate quantile sketch over a stream of $n$ inputs approximates the rank of any query point $q$ - that is, the number of input points less than $q$ - up to an additive error of $\varepsilon n$, generally with some probability of at least $1 - 1/\mathrm{poly}(n)$, while consuming $o(n)$ space. While the celebrated KLL sketch of Karnin, Lang, and Liberty achieves a provably optimal quantile approximation algorithm over worst-case streams, the approximations it achieves in practice are often far from optimal. Indeed, the most commonly used technique in practice is Dunning's t-digest, which often achieves much better approximations than KLL on real-world data but is known to have arbitrarily large errors in the worst case. We apply interpolation techniques to the streaming quantiles problem to attempt to achieve better approximations on real-world data sets than KLL while maintaining similar guarantees in the worst case.

Improved Space Bounds for Learning with Experts

We give improved tradeoffs between space and regret for the online learning with expert advice problem over $T$ days with $n$ experts. Given a space budget of $n^{\delta}$ for $\delta \in (0,1)$, we provide an algorithm achieving regret $\tilde{O}(n^2 T^{1/(1+\delta)})$, improving upon the regret bound $\tilde{O}(n^2 T^{2/(2+\delta)})$ in the recent work of [PZ23]. The improvement is particularly salient in the regime $\delta \rightarrow 1$ where the regret of our algorithm approaches $\tilde{O}_n(\sqrt{T})$, matching the $T$ dependence in the standard online setting without space restrictions.

Exponentially Improving the Complexity of Simulating the Weisfeiler-Lehman Test with Graph Neural Networks

Recent work shows that the expressive power of Graph Neural Networks (GNNs) in distinguishing non-isomorphic graphs is exactly the same as that of the Weisfeiler-Lehman (WL) graph test. In particular, they show that the WL test can be simulated by GNNs. However, those simulations involve neural networks for the 'combine' function of size polynomial or even exponential in the number of graph nodes $n$, as well as feature vectors of length linear in $n$. We present an improved simulation of the WL test on GNNs with \emph{exponentially} lower complexity. In particular, the neural network implementing the combine function in each node has only a polylogarithmic number of parameters in $n$, and the feature vectors exchanged by the nodes of GNN consists of only $O(\log n)$ bits. We also give logarithmic lower bounds for the feature vector length and the size of the neural networks, showing the (near)-optimality of our construction.