Sample-Efficient Private Learning of Mixtures of Gaussians

We study the problem of learning mixtures of Gaussians with approximate differential privacy. We prove that roughly $kd^2 + k^{1.5} d^{1.75} + k^2 d$ samples suffice to learn a mixture of $k$ arbitrary $d$-dimensional Gaussians up to low total variation distance, with differential privacy. Our work improves over the previous best result [AAL24b] (which required roughly $k^2 d^4$ samples) and is provably optimal when $d$ is much larger than $k^2$. Moreover, we give the first optimal bound for privately learning mixtures of $k$ univariate (i.e., $1$-dimensional) Gaussians. Importantly, we show that the sample complexity for privately learning mixtures of univariate Gaussians is linear in the number of components $k$, whereas the previous best sample complexity [AAL21] was quadratic in $k$. Our algorithms utilize various techniques, including the inverse sensitivity mechanism [AD20b, AD20a, HKMN23], sample compression for distributions [ABDH+20], and methods for bounding volumes of sumsets.

Statistical-Computational Trade-offs for Density Estimation

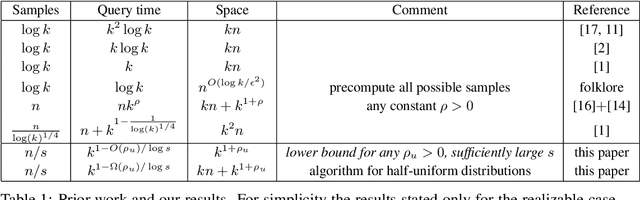
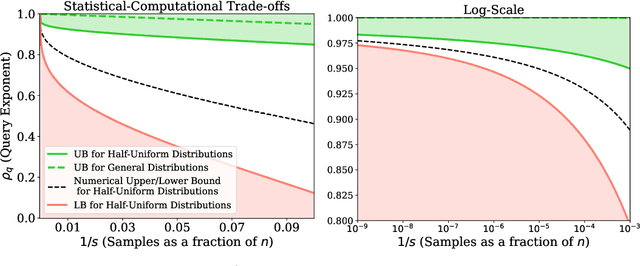
We study the density estimation problem defined as follows: given $k$ distributions $p_1, \ldots, p_k$ over a discrete domain $[n]$, as well as a collection of samples chosen from a ``query'' distribution $q$ over $[n]$, output $p_i$ that is ``close'' to $q$. Recently~\cite{aamand2023data} gave the first and only known result that achieves sublinear bounds in {\em both} the sampling complexity and the query time while preserving polynomial data structure space. However, their improvement over linear samples and time is only by subpolynomial factors. Our main result is a lower bound showing that, for a broad class of data structures, their bounds cannot be significantly improved. In particular, if an algorithm uses $O(n/\log^c k)$ samples for some constant $c>0$ and polynomial space, then the query time of the data structure must be at least $k^{1-O(1)/\log \log k}$, i.e., close to linear in the number of distributions $k$. This is a novel \emph{statistical-computational} trade-off for density estimation, demonstrating that any data structure must use close to a linear number of samples or take close to linear query time. The lower bound holds even in the realizable case where $q=p_i$ for some $i$, and when the distributions are flat (specifically, all distributions are uniform over half of the domain $[n]$). We also give a simple data structure for our lower bound instance with asymptotically matching upper bounds. Experiments show that the data structure is quite efficient in practice.

Improved algorithms for learning quantum Hamiltonians, via flat polynomials

We give an improved algorithm for learning a quantum Hamiltonian given copies of its Gibbs state, that can succeed at any temperature. Specifically, we improve over the work of Bakshi, Liu, Moitra, and Tang [BLMT24], by reducing the sample complexity and runtime dependence to singly exponential in the inverse-temperature parameter, as opposed to doubly exponential. Our main technical contribution is a new flat polynomial approximation to the exponential function, with significantly lower degree than the flat polynomial approximation used in [BLMT24].

Better and Simpler Lower Bounds for Differentially Private Statistical Estimation

We provide improved lower bounds for two well-known high-dimensional private estimation tasks. First, we prove that for estimating the covariance of a Gaussian up to spectral error $\alpha$ with approximate differential privacy, one needs $\tilde{\Omega}\left(\frac{d^{3/2}}{\alpha \varepsilon} + \frac{d}{\alpha^2}\right)$ samples for any $\alpha \le O(1)$, which is tight up to logarithmic factors. This improves over previous work which established this for $\alpha \le O\left(\frac{1}{\sqrt{d}}\right)$, and is also simpler than previous work. Next, we prove that for estimating the mean of a heavy-tailed distribution with bounded $k$th moments with approximate differential privacy, one needs $\tilde{\Omega}\left(\frac{d}{\alpha^{k/(k-1)} \varepsilon} + \frac{d}{\alpha^2}\right)$ samples. This matches known upper bounds and improves over the best known lower bound for this problem, which only hold for pure differential privacy, or when $k = 2$. Our techniques follow the method of fingerprinting and are generally quite simple. Our lower bound for heavy-tailed estimation is based on a black-box reduction from privately estimating identity-covariance Gaussians. Our lower bound for covariance estimation utilizes a Bayesian approach to show that, under an Inverse Wishart prior distribution for the covariance matrix, no private estimator can be accurate even in expectation, without sufficiently many samples.

SPAIC: A sub-$μ$W/Channel, 16-Channel General-Purpose Event-Based Analog Front-End with Dual-Mode Encoders

Low-power event-based analog front-ends (AFE) are a crucial component required to build efficient end-to-end neuromorphic processing systems for edge computing. Although several neuromorphic chips have been developed for implementing spiking neural networks (SNNs) and solving a wide range of sensory processing tasks, there are only a few general-purpose analog front-end devices that can be used to convert analog sensory signals into spikes and interfaced to neuromorphic processors. In this work, we present a novel, highly configurable analog front-end chip, denoted as SPAIC (signal-to-spike converter for analog AI computation), that offers a general-purpose dual-mode analog signal-to-spike encoding with delta modulation and pulse frequency modulation, with tunable frequency bands. The ASIC is designed in a 180 nm process. It supports and encodes a wide variety of signals spanning 4 orders of magnitude in frequency, and provides an event-based output that is compatible with existing neuromorphic processors. We validated the ASIC for its functions and present initial silicon measurement results characterizing the basic building blocks of the chip.

A faster and simpler algorithm for learning shallow networks

We revisit the well-studied problem of learning a linear combination of $k$ ReLU activations given labeled examples drawn from the standard $d$-dimensional Gaussian measure. Chen et al. [CDG+23] recently gave the first algorithm for this problem to run in $\text{poly}(d,1/\varepsilon)$ time when $k = O(1)$, where $\varepsilon$ is the target error. More precisely, their algorithm runs in time $(d/\varepsilon)^{\mathrm{quasipoly}(k)}$ and learns over multiple stages. Here we show that a much simpler one-stage version of their algorithm suffices, and moreover its runtime is only $(d/\varepsilon)^{O(k^2)}$.

Data Structures for Density Estimation

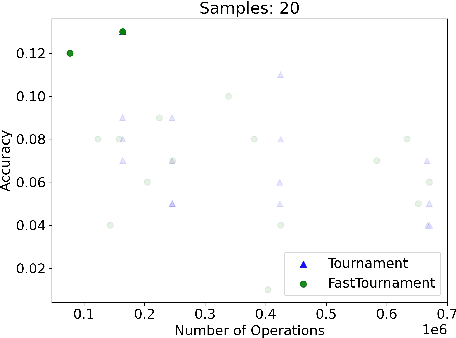
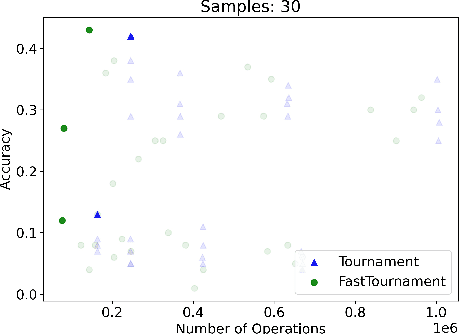
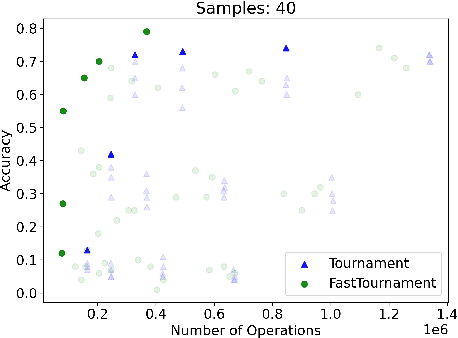
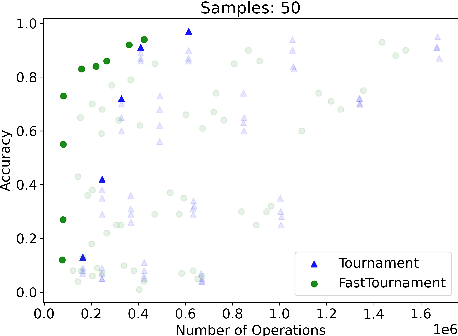
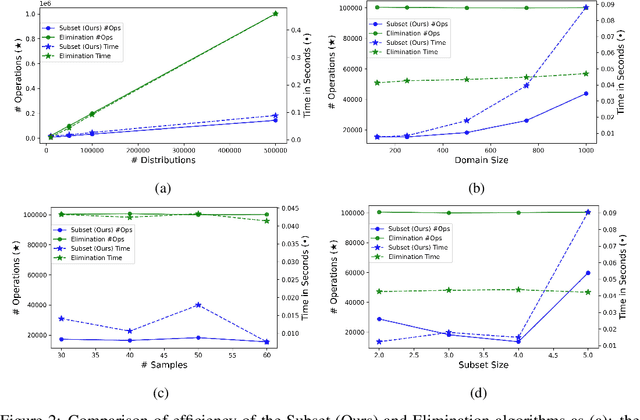
We study statistical/computational tradeoffs for the following density estimation problem: given $k$ distributions $v_1, \ldots, v_k$ over a discrete domain of size $n$, and sampling access to a distribution $p$, identify $v_i$ that is "close" to $p$. Our main result is the first data structure that, given a sublinear (in $n$) number of samples from $p$, identifies $v_i$ in time sublinear in $k$. We also give an improved version of the algorithm of Acharya et al. (2018) that reports $v_i$ in time linear in $k$. The experimental evaluation of the latter algorithm shows that it achieves a significant reduction in the number of operations needed to achieve a given accuracy compared to prior work.

Learned Interpolation for Better Streaming Quantile Approximation with Worst-Case Guarantees

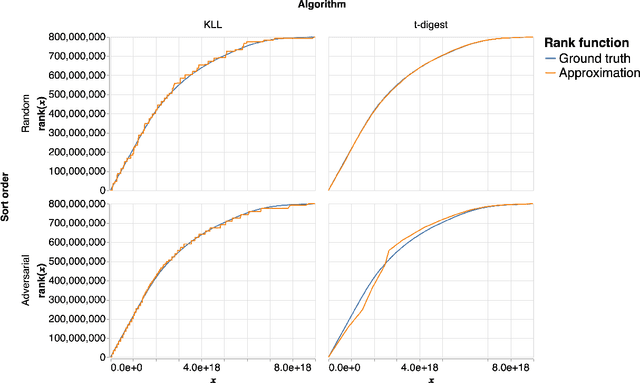
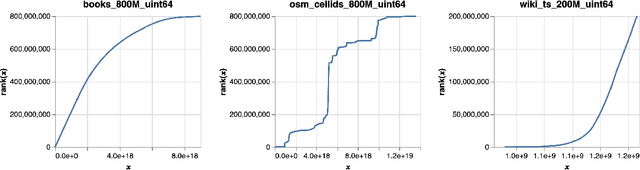
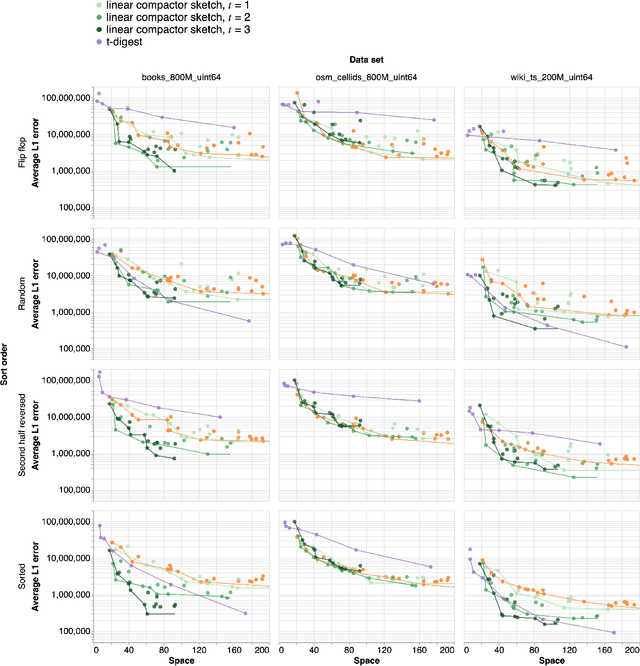
An $\varepsilon$-approximate quantile sketch over a stream of $n$ inputs approximates the rank of any query point $q$ - that is, the number of input points less than $q$ - up to an additive error of $\varepsilon n$, generally with some probability of at least $1 - 1/\mathrm{poly}(n)$, while consuming $o(n)$ space. While the celebrated KLL sketch of Karnin, Lang, and Liberty achieves a provably optimal quantile approximation algorithm over worst-case streams, the approximations it achieves in practice are often far from optimal. Indeed, the most commonly used technique in practice is Dunning's t-digest, which often achieves much better approximations than KLL on real-world data but is known to have arbitrarily large errors in the worst case. We apply interpolation techniques to the streaming quantiles problem to attempt to achieve better approximations on real-world data sets than KLL while maintaining similar guarantees in the worst case.

Krylov Methods are Optimal for Low-Rank Approximation

We consider the problem of rank-$1$ low-rank approximation (LRA) in the matrix-vector product model under various Schatten norms: $$ \min_{\|u\|_2=1} \|A (I - u u^\top)\|_{\mathcal{S}_p} , $$ where $\|M\|_{\mathcal{S}_p}$ denotes the $\ell_p$ norm of the singular values of $M$. Given $\varepsilon>0$, our goal is to output a unit vector $v$ such that $$ \|A(I - vv^\top)\|_{\mathcal{S}_p} \leq (1+\varepsilon) \min_{\|u\|_2=1}\|A(I - u u^\top)\|_{\mathcal{S}_p}. $$ Our main result shows that Krylov methods (nearly) achieve the information-theoretically optimal number of matrix-vector products for Spectral ($p=\infty$), Frobenius ($p=2$) and Nuclear ($p=1$) LRA. In particular, for Spectral LRA, we show that any algorithm requires $\Omega\left(\log(n)/\varepsilon^{1/2}\right)$ matrix-vector products, exactly matching the upper bound obtained by Krylov methods [MM15, BCW22]. Our lower bound addresses Open Question 1 in [Woo14], providing evidence for the lack of progress on algorithms for Spectral LRA and resolves Open Question 1.2 in [BCW22]. Next, we show that for any fixed constant $p$, i.e. $1\leq p =O(1)$, there is an upper bound of $O\left(\log(1/\varepsilon)/\varepsilon^{1/3}\right)$ matrix-vector products, implying that the complexity does not grow as a function of input size. This improves the $O\left(\log(n/\varepsilon)/\varepsilon^{1/3}\right)$ bound recently obtained in [BCW22], and matches their $\Omega\left(1/\varepsilon^{1/3}\right)$ lower bound, to a $\log(1/\varepsilon)$ factor.

Query lower bounds for log-concave sampling

Log-concave sampling has witnessed remarkable algorithmic advances in recent years, but the corresponding problem of proving lower bounds for this task has remained elusive, with lower bounds previously known only in dimension one. In this work, we establish the following query lower bounds: (1) sampling from strongly log-concave and log-smooth distributions in dimension $d\ge 2$ requires $\Omega(\log \kappa)$ queries, which is sharp in any constant dimension, and (2) sampling from Gaussians in dimension $d$ (hence also from general log-concave and log-smooth distributions in dimension $d$) requires $\widetilde \Omega(\min(\sqrt\kappa \log d, d))$ queries, which is nearly sharp for the class of Gaussians. Here $\kappa$ denotes the condition number of the target distribution. Our proofs rely upon (1) a multiscale construction inspired by work on the Kakeya conjecture in harmonic analysis, and (2) a novel reduction that demonstrates that block Krylov algorithms are optimal for this problem, as well as connections to lower bound techniques based on Wishart matrices developed in the matrix-vector query literature.