Learned Interpolation for Better Streaming Quantile Approximation with Worst-Case Guarantees
Paper and Code
Apr 15, 2023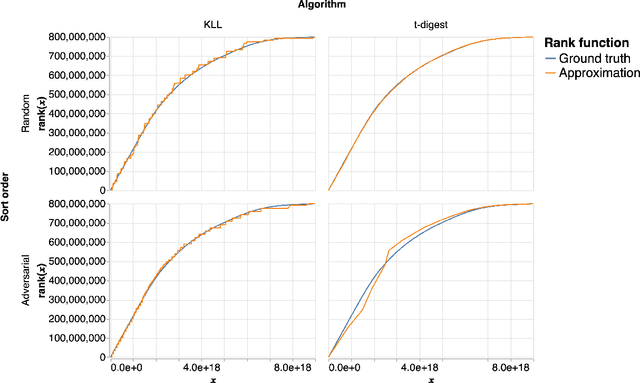
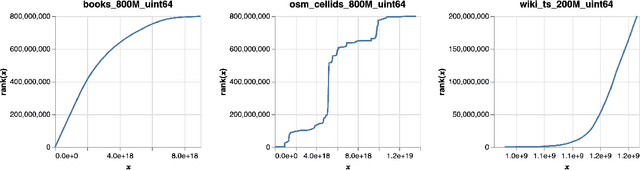

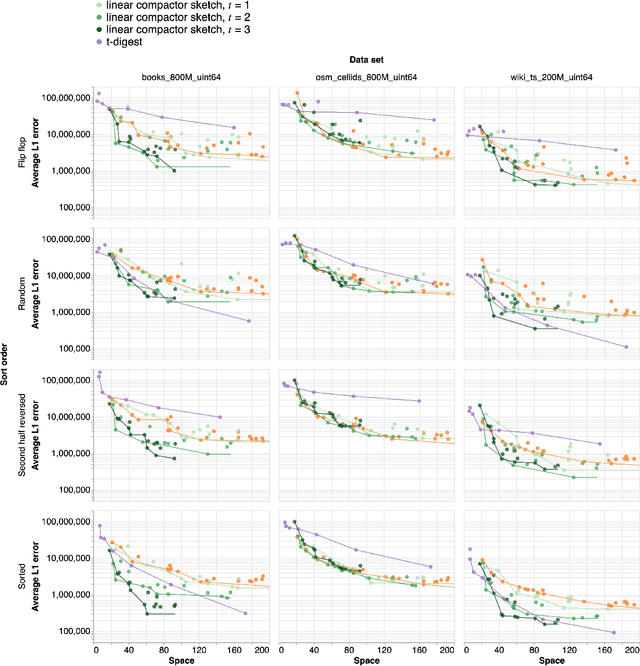
An $\varepsilon$-approximate quantile sketch over a stream of $n$ inputs approximates the rank of any query point $q$ - that is, the number of input points less than $q$ - up to an additive error of $\varepsilon n$, generally with some probability of at least $1 - 1/\mathrm{poly}(n)$, while consuming $o(n)$ space. While the celebrated KLL sketch of Karnin, Lang, and Liberty achieves a provably optimal quantile approximation algorithm over worst-case streams, the approximations it achieves in practice are often far from optimal. Indeed, the most commonly used technique in practice is Dunning's t-digest, which often achieves much better approximations than KLL on real-world data but is known to have arbitrarily large errors in the worst case. We apply interpolation techniques to the streaming quantiles problem to attempt to achieve better approximations on real-world data sets than KLL while maintaining similar guarantees in the worst case.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge