Optimal Algorithms for Augmented Testing of Discrete Distributions

We consider the problem of hypothesis testing for discrete distributions. In the standard model, where we have sample access to an underlying distribution $p$, extensive research has established optimal bounds for uniformity testing, identity testing (goodness of fit), and closeness testing (equivalence or two-sample testing). We explore these problems in a setting where a predicted data distribution, possibly derived from historical data or predictive machine learning models, is available. We demonstrate that such a predictor can indeed reduce the number of samples required for all three property testing tasks. The reduction in sample complexity depends directly on the predictor's quality, measured by its total variation distance from $p$. A key advantage of our algorithms is their adaptability to the precision of the prediction. Specifically, our algorithms can self-adjust their sample complexity based on the accuracy of the available prediction, operating without any prior knowledge of the estimation's accuracy (i.e. they are consistent). Additionally, we never use more samples than the standard approaches require, even if the predictions provide no meaningful information (i.e. they are also robust). We provide lower bounds to indicate that the improvements in sample complexity achieved by our algorithms are information-theoretically optimal. Furthermore, experimental results show that the performance of our algorithms on real data significantly exceeds our worst-case guarantees for sample complexity, demonstrating the practicality of our approach.

Statistical-Computational Trade-offs for Density Estimation

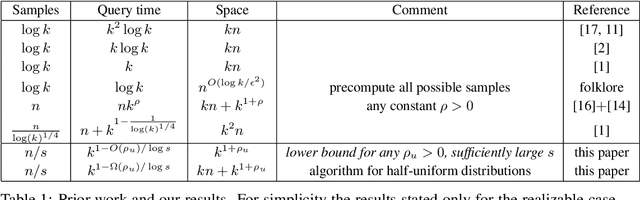
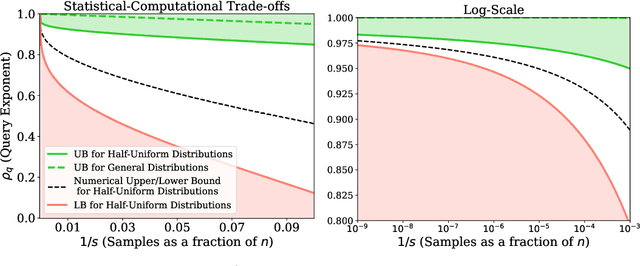
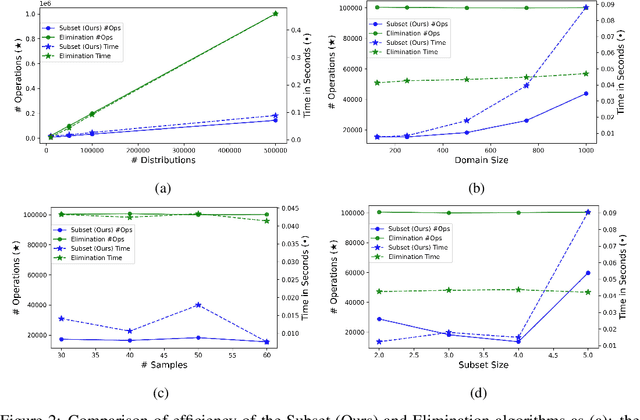
We study the density estimation problem defined as follows: given $k$ distributions $p_1, \ldots, p_k$ over a discrete domain $[n]$, as well as a collection of samples chosen from a ``query'' distribution $q$ over $[n]$, output $p_i$ that is ``close'' to $q$. Recently~\cite{aamand2023data} gave the first and only known result that achieves sublinear bounds in {\em both} the sampling complexity and the query time while preserving polynomial data structure space. However, their improvement over linear samples and time is only by subpolynomial factors. Our main result is a lower bound showing that, for a broad class of data structures, their bounds cannot be significantly improved. In particular, if an algorithm uses $O(n/\log^c k)$ samples for some constant $c>0$ and polynomial space, then the query time of the data structure must be at least $k^{1-O(1)/\log \log k}$, i.e., close to linear in the number of distributions $k$. This is a novel \emph{statistical-computational} trade-off for density estimation, demonstrating that any data structure must use close to a linear number of samples or take close to linear query time. The lower bound holds even in the realizable case where $q=p_i$ for some $i$, and when the distributions are flat (specifically, all distributions are uniform over half of the domain $[n]$). We also give a simple data structure for our lower bound instance with asymptotically matching upper bounds. Experiments show that the data structure is quite efficient in practice.

SparseCL: Sparse Contrastive Learning for Contradiction Retrieval

Contradiction retrieval refers to identifying and extracting documents that explicitly disagree with or refute the content of a query, which is important to many downstream applications like fact checking and data cleaning. To retrieve contradiction argument to the query from large document corpora, existing methods such as similarity search and crossencoder models exhibit significant limitations. The former struggles to capture the essence of contradiction due to its inherent nature of favoring similarity, while the latter suffers from computational inefficiency, especially when the size of corpora is large. To address these challenges, we introduce a novel approach: SparseCL that leverages specially trained sentence embeddings designed to preserve subtle, contradictory nuances between sentences. Our method utilizes a combined metric of cosine similarity and a sparsity function to efficiently identify and retrieve documents that contradict a given query. This approach dramatically enhances the speed of contradiction detection by reducing the need for exhaustive document comparisons to simple vector calculations. We validate our model using the Arguana dataset, a benchmark dataset specifically geared towards contradiction retrieval, as well as synthetic contradictions generated from the MSMARCO and HotpotQA datasets using GPT-4. Our experiments demonstrate the efficacy of our approach not only in contradiction retrieval with more than 30% accuracy improvements on MSMARCO and HotpotQA across different model architectures but also in applications such as cleaning corrupted corpora to restore high-quality QA retrieval. This paper outlines a promising direction for improving the accuracy and efficiency of contradiction retrieval in large-scale text corpora.

A Bi-metric Framework for Fast Similarity Search

We propose a new "bi-metric" framework for designing nearest neighbor data structures. Our framework assumes two dissimilarity functions: a ground-truth metric that is accurate but expensive to compute, and a proxy metric that is cheaper but less accurate. In both theory and practice, we show how to construct data structures using only the proxy metric such that the query procedure achieves the accuracy of the expensive metric, while only using a limited number of calls to both metrics. Our theoretical results instantiate this framework for two popular nearest neighbor search algorithms: DiskANN and Cover Tree. In both cases we show that, as long as the proxy metric used to construct the data structure approximates the ground-truth metric up to a bounded factor, our data structure achieves arbitrarily good approximation guarantees with respect to the ground-truth metric. On the empirical side, we apply the framework to the text retrieval problem with two dissimilarity functions evaluated by ML models with vastly different computational costs. We observe that for almost all data sets in the MTEB benchmark, our approach achieves a considerably better accuracy-efficiency tradeoff than the alternatives, such as re-ranking.

Worst-case Performance of Popular Approximate Nearest Neighbor Search Implementations: Guarantees and Limitations

Graph-based approaches to nearest neighbor search are popular and powerful tools for handling large datasets in practice, but they have limited theoretical guarantees. We study the worst-case performance of recent graph-based approximate nearest neighbor search algorithms, such as HNSW, NSG and DiskANN. For DiskANN, we show that its "slow preprocessing" version provably supports approximate nearest neighbor search query with constant approximation ratio and poly-logarithmic query time, on data sets with bounded "intrinsic" dimension. For the other data structure variants studied, including DiskANN with "fast preprocessing", HNSW and NSG, we present a family of instances on which the empirical query time required to achieve a "reasonable" accuracy is linear in instance size. For example, for DiskANN, we show that the query procedure can take at least $0.1 n$ steps on instances of size $n$ before it encounters any of the $5$ nearest neighbors of the query.

A Near-Linear Time Algorithm for the Chamfer Distance

For any two point sets $A,B \subset \mathbb{R}^d$ of size up to $n$, the Chamfer distance from $A$ to $B$ is defined as $\text{CH}(A,B)=\sum_{a \in A} \min_{b \in B} d_X(a,b)$, where $d_X$ is the underlying distance measure (e.g., the Euclidean or Manhattan distance). The Chamfer distance is a popular measure of dissimilarity between point clouds, used in many machine learning, computer vision, and graphics applications, and admits a straightforward $O(d n^2)$-time brute force algorithm. Further, the Chamfer distance is often used as a proxy for the more computationally demanding Earth-Mover (Optimal Transport) Distance. However, the \emph{quadratic} dependence on $n$ in the running time makes the naive approach intractable for large datasets. We overcome this bottleneck and present the first $(1+\epsilon)$-approximate algorithm for estimating the Chamfer distance with a near-linear running time. Specifically, our algorithm runs in time $O(nd \log (n)/\varepsilon^2)$ and is implementable. Our experiments demonstrate that it is both accurate and fast on large high-dimensional datasets. We believe that our algorithm will open new avenues for analyzing large high-dimensional point clouds. We also give evidence that if the goal is to \emph{report} a $(1+\varepsilon)$-approximate mapping from $A$ to $B$ (as opposed to just its value), then any sub-quadratic time algorithm is unlikely to exist.

Data Structures for Density Estimation

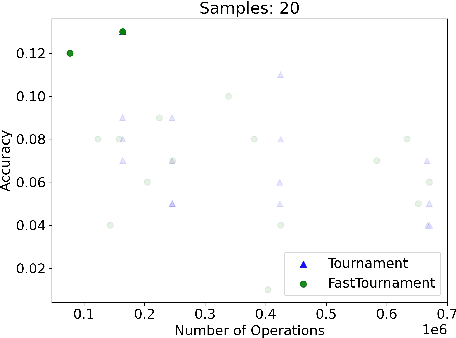
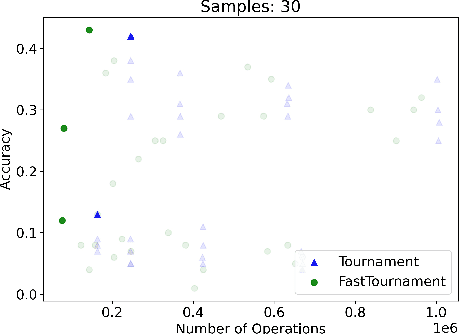
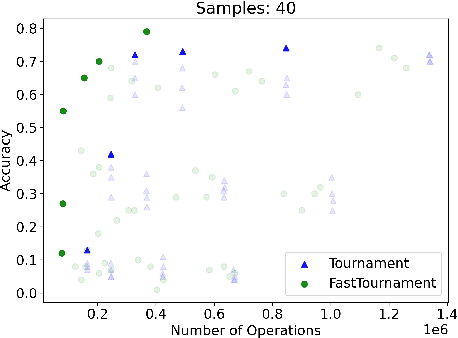
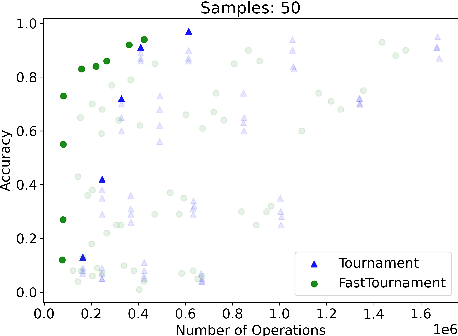
We study statistical/computational tradeoffs for the following density estimation problem: given $k$ distributions $v_1, \ldots, v_k$ over a discrete domain of size $n$, and sampling access to a distribution $p$, identify $v_i$ that is "close" to $p$. Our main result is the first data structure that, given a sublinear (in $n$) number of samples from $p$, identifies $v_i$ in time sublinear in $k$. We also give an improved version of the algorithm of Acharya et al. (2018) that reports $v_i$ in time linear in $k$. The experimental evaluation of the latter algorithm shows that it achieves a significant reduction in the number of operations needed to achieve a given accuracy compared to prior work.

Learned Interpolation for Better Streaming Quantile Approximation with Worst-Case Guarantees

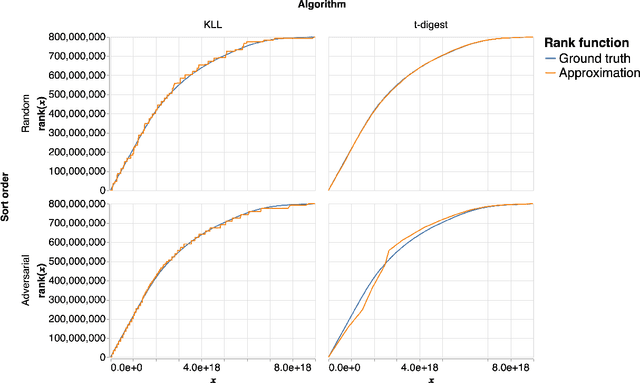
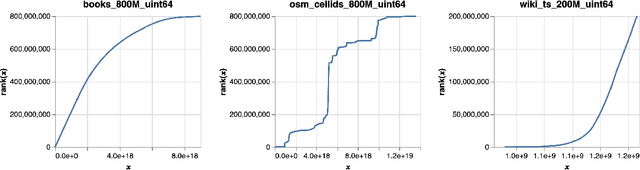
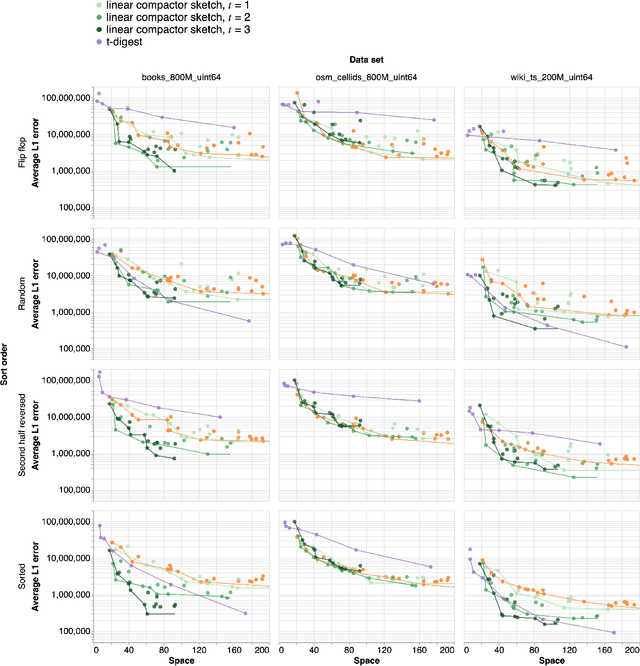
An $\varepsilon$-approximate quantile sketch over a stream of $n$ inputs approximates the rank of any query point $q$ - that is, the number of input points less than $q$ - up to an additive error of $\varepsilon n$, generally with some probability of at least $1 - 1/\mathrm{poly}(n)$, while consuming $o(n)$ space. While the celebrated KLL sketch of Karnin, Lang, and Liberty achieves a provably optimal quantile approximation algorithm over worst-case streams, the approximations it achieves in practice are often far from optimal. Indeed, the most commonly used technique in practice is Dunning's t-digest, which often achieves much better approximations than KLL on real-world data but is known to have arbitrarily large errors in the worst case. We apply interpolation techniques to the streaming quantiles problem to attempt to achieve better approximations on real-world data sets than KLL while maintaining similar guarantees in the worst case.

Sub-quadratic Algorithms for Kernel Matrices via Kernel Density Estimation

Kernel matrices, as well as weighted graphs represented by them, are ubiquitous objects in machine learning, statistics and other related fields. The main drawback of using kernel methods (learning and inference using kernel matrices) is efficiency -- given $n$ input points, most kernel-based algorithms need to materialize the full $n \times n$ kernel matrix before performing any subsequent computation, thus incurring $\Omega(n^2)$ runtime. Breaking this quadratic barrier for various problems has therefore, been a subject of extensive research efforts. We break the quadratic barrier and obtain $\textit{subquadratic}$ time algorithms for several fundamental linear-algebraic and graph processing primitives, including approximating the top eigenvalue and eigenvector, spectral sparsification, solving linear systems, local clustering, low-rank approximation, arboricity estimation and counting weighted triangles. We build on the recent Kernel Density Estimation framework, which (after preprocessing in time subquadratic in $n$) can return estimates of row/column sums of the kernel matrix. In particular, we develop efficient reductions from $\textit{weighted vertex}$ and $\textit{weighted edge sampling}$ on kernel graphs, $\textit{simulating random walks}$ on kernel graphs, and $\textit{importance sampling}$ on matrices to Kernel Density Estimation and show that we can generate samples from these distributions in $\textit{sublinear}$ (in the support of the distribution) time. Our reductions are the central ingredient in each of our applications and we believe they may be of independent interest. We empirically demonstrate the efficacy of our algorithms on low-rank approximation (LRA) and spectral sparsification, where we observe a $\textbf{9x}$ decrease in the number of kernel evaluations over baselines for LRA and a $\textbf{41x}$ reduction in the graph size for spectral sparsification.

Exponentially Improving the Complexity of Simulating the Weisfeiler-Lehman Test with Graph Neural Networks

Recent work shows that the expressive power of Graph Neural Networks (GNNs) in distinguishing non-isomorphic graphs is exactly the same as that of the Weisfeiler-Lehman (WL) graph test. In particular, they show that the WL test can be simulated by GNNs. However, those simulations involve neural networks for the 'combine' function of size polynomial or even exponential in the number of graph nodes $n$, as well as feature vectors of length linear in $n$. We present an improved simulation of the WL test on GNNs with \emph{exponentially} lower complexity. In particular, the neural network implementing the combine function in each node has only a polylogarithmic number of parameters in $n$, and the feature vectors exchanged by the nodes of GNN consists of only $O(\log n)$ bits. We also give logarithmic lower bounds for the feature vector length and the size of the neural networks, showing the (near)-optimality of our construction.