Provably Extracting the Features from a General Superposition

It is widely believed that complex machine learning models generally encode features through linear representations, but these features exist in superposition, making them challenging to recover. We study the following fundamental setting for learning features in superposition from black-box query access: we are given query access to a function \[ f(x)=\sum_{i=1}^n a_i\,σ_i(v_i^\top x), \] where each unit vector $v_i$ encodes a feature direction and $σ_i:\mathbb{R} \rightarrow \mathbb{R}$ is an arbitrary response function and our goal is to recover the $v_i$ and the function $f$. In learning-theoretic terms, superposition refers to the overcomplete regime, when the number of features is larger than the underlying dimension (i.e. $n > d$), which has proven especially challenging for typical algorithmic approaches. Our main result is an efficient query algorithm that, from noisy oracle access to $f$, identifies all feature directions whose responses are non-degenerate and reconstructs the function $f$. Crucially, our algorithm works in a significantly more general setting than all related prior results -- we allow for essentially arbitrary superpositions, only requiring that $v_i, v_j$ are not nearly identical for $i \neq j$, and general response functions $σ_i$. At a high level, our algorithm introduces an approach for searching in Fourier space by iteratively refining the search space to locate the hidden directions $v_i$.

Provably Learning from Modern Language Models via Low Logit Rank

While modern language models and their inner workings are incredibly complex, recent work (Golowich, Liu & Shetty; 2025) has proposed a simple and potentially tractable abstraction for them through the observation that empirically, these language models all seem to have approximately low logit rank. Roughly, this means that a matrix formed by the model's log probabilities of various tokens conditioned on certain sequences of tokens is well approximated by a low rank matrix. In this paper, our focus is on understanding how this structure can be exploited algorithmically for obtaining provable learning guarantees. Since low logit rank models can encode hard-to-learn distributions such as noisy parities, we study a query learning model with logit queries that reflects the access model for common APIs. Our main result is an efficient algorithm for learning any approximately low logit rank model from queries. We emphasize that our structural assumption closely reflects the behavior that is empirically observed in modern language models. Thus, our result gives what we believe is the first end-to-end learning guarantee for a generative model that plausibly captures modern language models.

Are LLMs complicated ethical dilemma analyzers?

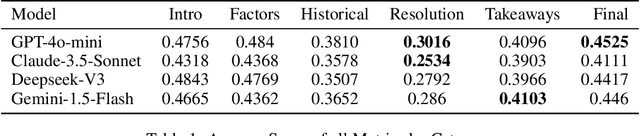
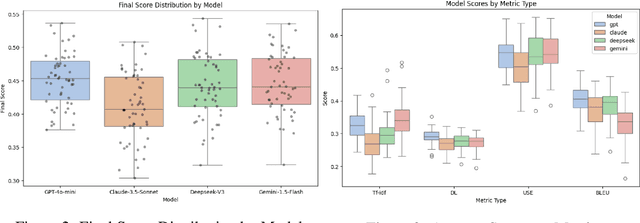
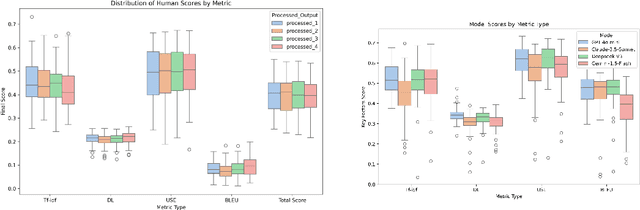
One open question in the study of Large Language Models (LLMs) is whether they can emulate human ethical reasoning and act as believable proxies for human judgment. To investigate this, we introduce a benchmark dataset comprising 196 real-world ethical dilemmas and expert opinions, each segmented into five structured components: Introduction, Key Factors, Historical Theoretical Perspectives, Resolution Strategies, and Key Takeaways. We also collect non-expert human responses for comparison, limited to the Key Factors section due to their brevity. We evaluate multiple frontier LLMs (GPT-4o-mini, Claude-3.5-Sonnet, Deepseek-V3, Gemini-1.5-Flash) using a composite metric framework based on BLEU, Damerau-Levenshtein distance, TF-IDF cosine similarity, and Universal Sentence Encoder similarity. Metric weights are computed through an inversion-based ranking alignment and pairwise AHP analysis, enabling fine-grained comparison of model outputs to expert responses. Our results show that LLMs generally outperform non-expert humans in lexical and structural alignment, with GPT-4o-mini performing most consistently across all sections. However, all models struggle with historical grounding and proposing nuanced resolution strategies, which require contextual abstraction. Human responses, while less structured, occasionally achieve comparable semantic similarity, suggesting intuitive moral reasoning. These findings highlight both the strengths and current limitations of LLMs in ethical decision-making.

Model Stealing for Any Low-Rank Language Model

Model stealing, where a learner tries to recover an unknown model via carefully chosen queries, is a critical problem in machine learning, as it threatens the security of proprietary models and the privacy of data they are trained on. In recent years, there has been particular interest in stealing large language models (LLMs). In this paper, we aim to build a theoretical understanding of stealing language models by studying a simple and mathematically tractable setting. We study model stealing for Hidden Markov Models (HMMs), and more generally low-rank language models. We assume that the learner works in the conditional query model, introduced by Kakade, Krishnamurthy, Mahajan and Zhang. Our main result is an efficient algorithm in the conditional query model, for learning any low-rank distribution. In other words, our algorithm succeeds at stealing any language model whose output distribution is low-rank. This improves upon the previous result by Kakade, Krishnamurthy, Mahajan and Zhang, which also requires the unknown distribution to have high "fidelity", a property that holds only in restricted cases. There are two key insights behind our algorithm: First, we represent the conditional distributions at each timestep by constructing barycentric spanners among a collection of vectors of exponentially large dimension. Second, for sampling from our representation, we iteratively solve a sequence of convex optimization problems that involve projection in relative entropy to prevent compounding of errors over the length of the sequence. This is an interesting example where, at least theoretically, allowing a machine learning model to solve more complex problems at inference time can lead to drastic improvements in its performance.

Optimal high-precision shadow estimation

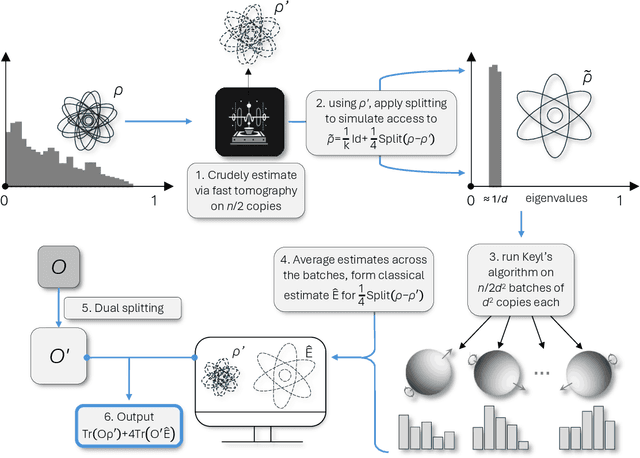
We give the first tight sample complexity bounds for shadow tomography and classical shadows in the regime where the target error is below some sufficiently small inverse polynomial in the dimension of the Hilbert space. Formally we give a protocol that, given any $m\in\mathbb{N}$ and $\epsilon \le O(d^{-12})$, measures $O(\log(m)/\epsilon^2)$ copies of an unknown mixed state $\rho\in\mathbb{C}^{d\times d}$ and outputs a classical description of $\rho$ which can then be used to estimate any collection of $m$ observables to within additive accuracy $\epsilon$. Previously, even for the simpler task of shadow tomography -- where the $m$ observables are known in advance -- the best known rates either scaled benignly but suboptimally in all of $m, d, \epsilon$, or scaled optimally in $\epsilon, m$ but had additional polynomial factors in $d$ for general observables. Intriguingly, we also show via dimensionality reduction, that we can rescale $\epsilon$ and $d$ to reduce to the regime where $\epsilon \le O(d^{-1/2})$. Our algorithm draws upon representation-theoretic tools recently developed in the context of full state tomography.

Structure learning of Hamiltonians from real-time evolution

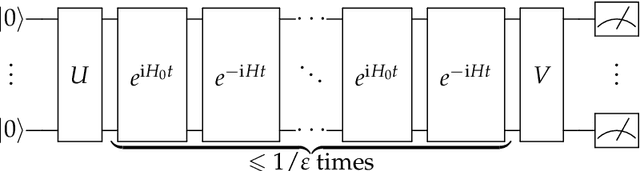
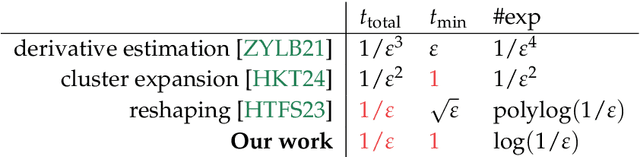
We initiate the study of Hamiltonian structure learning from real-time evolution: given the ability to apply $e^{-\mathrm{i} Ht}$ for an unknown local Hamiltonian $H = \sum_{a = 1}^m \lambda_a E_a$ on $n$ qubits, the goal is to recover $H$. This problem is already well-studied under the assumption that the interaction terms, $E_a$, are given, and only the interaction strengths, $\lambda_a$, are unknown. But is it possible to learn a local Hamiltonian without prior knowledge of its interaction structure? We present a new, general approach to Hamiltonian learning that not only solves the challenging structure learning variant, but also resolves other open questions in the area, all while achieving the gold standard of Heisenberg-limited scaling. In particular, our algorithm recovers the Hamiltonian to $\varepsilon$ error with an evolution time scaling with $1/\varepsilon$, and has the following appealing properties: (1) it does not need to know the Hamiltonian terms; (2) it works beyond the short-range setting, extending to any Hamiltonian $H$ where the sum of terms interacting with a qubit has bounded norm; (3) it evolves according to $H$ in constant time $t$ increments, thus achieving constant time resolution. To our knowledge, no prior algorithm with Heisenberg-limited scaling existed with even one of these properties. As an application, we can also learn Hamiltonians exhibiting power-law decay up to accuracy $\varepsilon$ with total evolution time beating the standard limit of $1/\varepsilon^2$.

An optimal tradeoff between entanglement and copy complexity for state tomography

There has been significant interest in understanding how practical constraints on contemporary quantum devices impact the complexity of quantum learning. For the classic question of tomography, recent work tightly characterized the copy complexity for any protocol that can only measure one copy of the unknown state at a time, showing it is polynomially worse than if one can make fully-entangled measurements. While we now have a fairly complete picture of the rates for such tasks in the near-term and fault-tolerant regimes, it remains poorly understood what the landscape in between looks like. In this work, we study tomography in the natural setting where one can make measurements of $t$ copies at a time. For sufficiently small $\epsilon$, we show that for any $t \le d^2$, $\widetilde{\Theta}(\frac{d^3}{\sqrt{t}\epsilon^2})$ copies are necessary and sufficient to learn an unknown $d$-dimensional state $\rho$ to trace distance $\epsilon$. This gives a smooth and optimal interpolation between the known rates for single-copy and fully-entangled measurements. To our knowledge, this is the first smooth entanglement-copy tradeoff known for any quantum learning task, and for tomography, no intermediate point on this curve was known, even at $t = 2$. An important obstacle is that unlike the optimal single-copy protocol, the optimal fully-entangled protocol is inherently biased and thus precludes naive batching approaches. Instead, we devise a novel two-stage procedure that uses Keyl's algorithm to refine a crude estimate for $\rho$ based on single-copy measurements. A key insight is to use Schur-Weyl sampling not to estimate the spectrum of $\rho$, but to estimate the deviation of $\rho$ from the maximally mixed state. When $\rho$ is far from the maximally mixed state, we devise a novel quantum splitting procedure that reduces to the case where $\rho$ is close to maximally mixed.

Learning quantum Hamiltonians at any temperature in polynomial time

We study the problem of learning a local quantum Hamiltonian $H$ given copies of its Gibbs state $\rho = e^{-\beta H}/\textrm{tr}(e^{-\beta H})$ at a known inverse temperature $\beta>0$. Anshu, Arunachalam, Kuwahara, and Soleimanifar (arXiv:2004.07266) gave an algorithm to learn a Hamiltonian on $n$ qubits to precision $\epsilon$ with only polynomially many copies of the Gibbs state, but which takes exponential time. Obtaining a computationally efficient algorithm has been a major open problem [Alhambra'22 (arXiv:2204.08349)], [Anshu, Arunachalam'22 (arXiv:2204.08349)], with prior work only resolving this in the limited cases of high temperature [Haah, Kothari, Tang'21 (arXiv:2108.04842)] or commuting terms [Anshu, Arunachalam, Kuwahara, Soleimanifar'21]. We fully resolve this problem, giving a polynomial time algorithm for learning $H$ to precision $\epsilon$ from polynomially many copies of the Gibbs state at any constant $\beta > 0$. Our main technical contribution is a new flat polynomial approximation to the exponential function, and a translation between multi-variate scalar polynomials and nested commutators. This enables us to formulate Hamiltonian learning as a polynomial system. We then show that solving a low-degree sum-of-squares relaxation of this polynomial system suffices to accurately learn the Hamiltonian.

Constant Approximation for Individual Preference Stable Clustering

Individual preference (IP) stability, introduced by Ahmadi et al. (ICML 2022), is a natural clustering objective inspired by stability and fairness constraints. A clustering is $\alpha$-IP stable if the average distance of every data point to its own cluster is at most $\alpha$ times the average distance to any other cluster. Unfortunately, determining if a dataset admits a $1$-IP stable clustering is NP-Hard. Moreover, before this work, it was unknown if an $o(n)$-IP stable clustering always \emph{exists}, as the prior state of the art only guaranteed an $O(n)$-IP stable clustering. We close this gap in understanding and show that an $O(1)$-IP stable clustering always exists for general metrics, and we give an efficient algorithm which outputs such a clustering. We also introduce generalizations of IP stability beyond average distance and give efficient, near-optimal algorithms in the cases where we consider the maximum and minimum distances within and between clusters.

Matrix Completion in Almost-Verification Time

We give a new framework for solving the fundamental problem of low-rank matrix completion, i.e., approximating a rank-$r$ matrix $\mathbf{M} \in \mathbb{R}^{m \times n}$ (where $m \ge n$) from random observations. First, we provide an algorithm which completes $\mathbf{M}$ on $99\%$ of rows and columns under no further assumptions on $\mathbf{M}$ from $\approx mr$ samples and using $\approx mr^2$ time. Then, assuming the row and column spans of $\mathbf{M}$ satisfy additional regularity properties, we show how to boost this partial completion guarantee to a full matrix completion algorithm by aggregating solutions to regression problems involving the observations. In the well-studied setting where $\mathbf{M}$ has incoherent row and column spans, our algorithms complete $\mathbf{M}$ to high precision from $mr^{2+o(1)}$ observations in $mr^{3 + o(1)}$ time (omitting logarithmic factors in problem parameters), improving upon the prior state-of-the-art [JN15] which used $\approx mr^5$ samples and $\approx mr^7$ time. Under an assumption on the row and column spans of $\mathbf{M}$ we introduce (which is satisfied by random subspaces with high probability), our sample complexity improves to an almost information-theoretically optimal $mr^{1 + o(1)}$, and our runtime improves to $mr^{2 + o(1)}$. Our runtimes have the appealing property of matching the best known runtime to verify that a rank-$r$ decomposition $\mathbf{U}\mathbf{V}^\top$ agrees with the sampled observations. We also provide robust variants of our algorithms that, given random observations from $\mathbf{M} + \mathbf{N}$ with $\|\mathbf{N}\|_{F} \le \Delta$, complete $\mathbf{M}$ to Frobenius norm distance $\approx r^{1.5}\Delta$ in the same runtimes as the noiseless setting. Prior noisy matrix completion algorithms [CP10] only guaranteed a distance of $\approx \sqrt{n}\Delta$.