Improved Frequency Estimation Algorithms with and without Predictions

Estimating frequencies of elements appearing in a data stream is a key task in large-scale data analysis. Popular sketching approaches to this problem (e.g., CountMin and CountSketch) come with worst-case guarantees that probabilistically bound the error of the estimated frequencies for any possible input. The work of Hsu et al. (2019) introduced the idea of using machine learning to tailor sketching algorithms to the specific data distribution they are being run on. In particular, their learning-augmented frequency estimation algorithm uses a learned heavy-hitter oracle which predicts which elements will appear many times in the stream. We give a novel algorithm, which in some parameter regimes, already theoretically outperforms the learning based algorithm of Hsu et al. without the use of any predictions. Augmenting our algorithm with heavy-hitter predictions further reduces the error and improves upon the state of the art. Empirically, our algorithms achieve superior performance in all experiments compared to prior approaches.

Improved Space Bounds for Learning with Experts

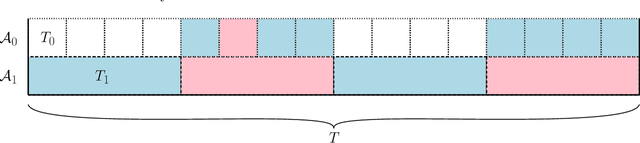
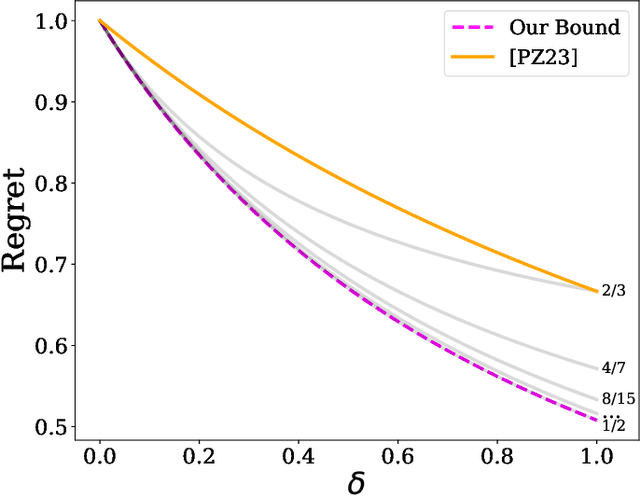
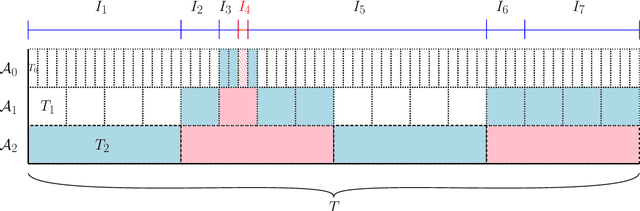
We give improved tradeoffs between space and regret for the online learning with expert advice problem over $T$ days with $n$ experts. Given a space budget of $n^{\delta}$ for $\delta \in (0,1)$, we provide an algorithm achieving regret $\tilde{O}(n^2 T^{1/(1+\delta)})$, improving upon the regret bound $\tilde{O}(n^2 T^{2/(2+\delta)})$ in the recent work of [PZ23]. The improvement is particularly salient in the regime $\delta \rightarrow 1$ where the regret of our algorithm approaches $\tilde{O}_n(\sqrt{T})$, matching the $T$ dependence in the standard online setting without space restrictions.

High Probability Convergence of Stochastic Gradient Methods

In this work, we describe a generic approach to show convergence with high probability for both stochastic convex and non-convex optimization with sub-Gaussian noise. In previous works for convex optimization, either the convergence is only in expectation or the bound depends on the diameter of the domain. Instead, we show high probability convergence with bounds depending on the initial distance to the optimal solution. The algorithms use step sizes analogous to the standard settings and are universal to Lipschitz functions, smooth functions, and their linear combinations. This method can be applied to the non-convex case. We demonstrate an $O((1+\sigma^{2}\log(1/\delta))/T+\sigma/\sqrt{T})$ convergence rate when the number of iterations $T$ is known and an $O((1+\sigma^{2}\log(T/\delta))/\sqrt{T})$ convergence rate when $T$ is unknown for SGD, where $1-\delta$ is the desired success probability. These bounds improve over existing bounds in the literature. Additionally, we demonstrate that our techniques can be used to obtain high probability bound for AdaGrad-Norm (Ward et al., 2019) that removes the bounded gradients assumption from previous works. Furthermore, our technique for AdaGrad-Norm extends to the standard per-coordinate AdaGrad algorithm (Duchi et al., 2011), providing the first noise-adapted high probability convergence for AdaGrad.

Improved Learning-augmented Algorithms for k-means and k-medians Clustering

We consider the problem of clustering in the learning-augmented setting, where we are given a data set in $d$-dimensional Euclidean space, and a label for each data point given by an oracle indicating what subsets of points should be clustered together. This setting captures situations where we have access to some auxiliary information about the data set relevant for our clustering objective, for instance the labels output by a neural network. Following prior work, we assume that there are at most an $\alpha \in (0,c)$ for some $c<1$ fraction of false positives and false negatives in each predicted cluster, in the absence of which the labels would attain the optimal clustering cost $\mathrm{OPT}$. For a dataset of size $m$, we propose a deterministic $k$-means algorithm that produces centers with improved bound on clustering cost compared to the previous randomized algorithm while preserving the $O( d m \log m)$ runtime. Furthermore, our algorithm works even when the predictions are not very accurate, i.e. our bound holds for $\alpha$ up to $1/2$, an improvement over $\alpha$ being at most $1/7$ in the previous work. For the $k$-medians problem we improve upon prior work by achieving a biquadratic improvement in the dependence of the approximation factor on the accuracy parameter $\alpha$ to get a cost of $(1+O(\alpha))\mathrm{OPT}$, while requiring essentially just $O(md \log^3 m/\alpha)$ runtime.

Streaming Submodular Maximization with Differential Privacy

In this work, we study the problem of privately maximizing a submodular function in the streaming setting. Extensive work has been done on privately maximizing submodular functions in the general case when the function depends upon the private data of individuals. However, when the size of the data stream drawn from the domain of the objective function is large or arrives very fast, one must privately optimize the objective within the constraints of the streaming setting. We establish fundamental differentially private baselines for this problem and then derive better trade-offs between privacy and utility for the special case of decomposable submodular functions. A submodular function is decomposable when it can be written as a sum of submodular functions; this structure arises naturally when each summand function models the utility of an individual and the goal is to study the total utility of the whole population as in the well-known Combinatorial Public Projects Problem. Finally, we complement our theoretical analysis with experimental corroboration.

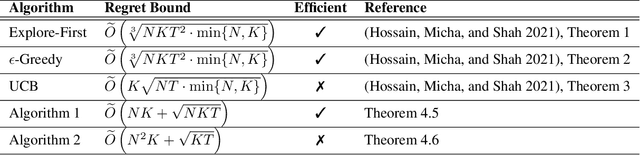
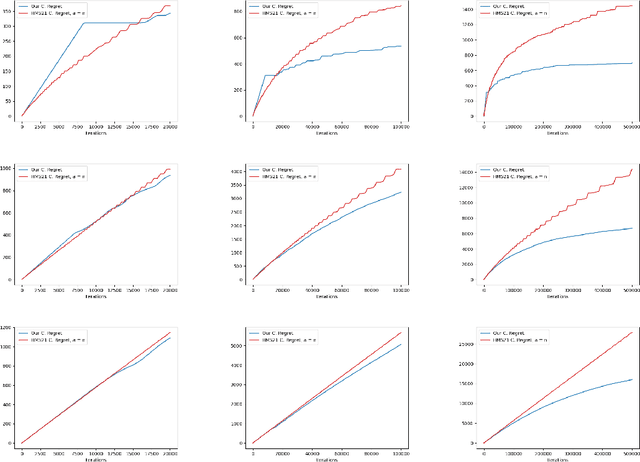
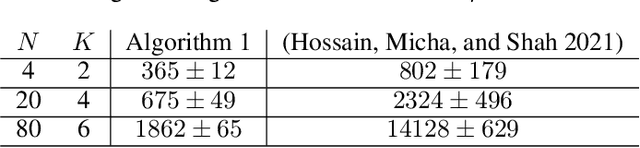
An Efficient Algorithm for Fair Multi-Agent Multi-Armed Bandit with Low Regret

Recently a multi-agent variant of the classical multi-armed bandit was proposed to tackle fairness issues in online learning. Inspired by a long line of work in social choice and economics, the goal is to optimize the Nash social welfare instead of the total utility. Unfortunately previous algorithms either are not efficient or achieve sub-optimal regret in terms of the number of rounds $T$. We propose a new efficient algorithm with lower regret than even previous inefficient ones. For $N$ agents, $K$ arms, and $T$ rounds, our approach has a regret bound of $\tilde{O}(\sqrt{NKT} + NK)$. This is an improvement to the previous approach, which has regret bound of $\tilde{O}( \min(NK, \sqrt{N} K^{3/2})\sqrt{T})$. We also complement our efficient algorithm with an inefficient approach with $\tilde{O}(\sqrt{KT} + N^2K)$ regret. The experimental findings confirm the effectiveness of our efficient algorithm compared to the previous approaches.

Private Frequency Estimation via Projective Geometry

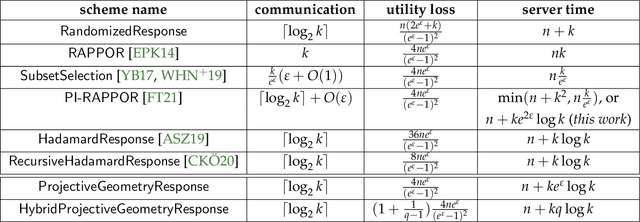
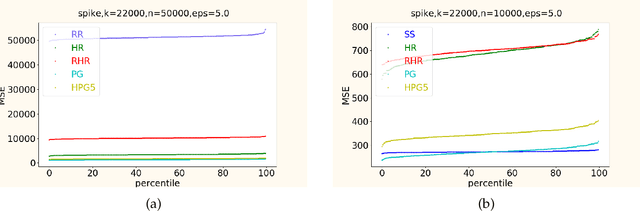
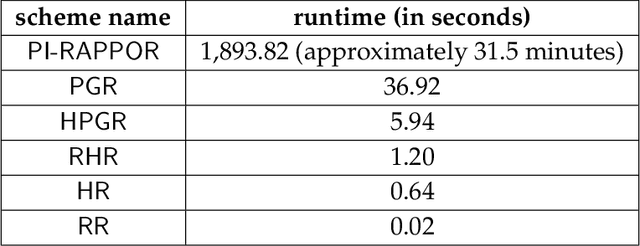
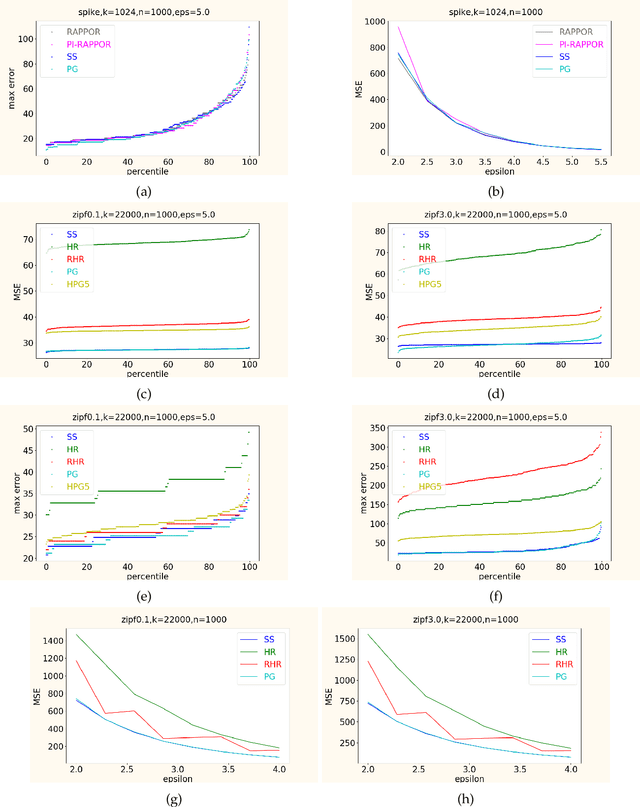
In this work, we propose a new algorithm ProjectiveGeometryResponse (PGR) for locally differentially private (LDP) frequency estimation. For a universe size of $k$ and with $n$ users, our $\varepsilon$-LDP algorithm has communication cost $\lceil\log_2k\rceil$ bits in the private coin setting and $\varepsilon\log_2 e + O(1)$ in the public coin setting, and has computation cost $O(n + k\exp(\varepsilon) \log k)$ for the server to approximately reconstruct the frequency histogram, while achieving the state-of-the-art privacy-utility tradeoff. In many parameter settings used in practice this is a significant improvement over the $ O(n+k^2)$ computation cost that is achieved by the recent PI-RAPPOR algorithm (Feldman and Talwar; 2021). Our empirical evaluation shows a speedup of over 50x over PI-RAPPOR while using approximately 75x less memory for practically relevant parameter settings. In addition, the running time of our algorithm is within an order of magnitude of HadamardResponse (Acharya, Sun, and Zhang; 2019) and RecursiveHadamardResponse (Chen, Kairouz, and Ozgur; 2020) which have significantly worse reconstruction error. The error of our algorithm essentially matches that of the communication- and time-inefficient but utility-optimal SubsetSelection (SS) algorithm (Ye and Barg; 2017). Our new algorithm is based on using Projective Planes over a finite field to define a small collection of sets that are close to being pairwise independent and a dynamic programming algorithm for approximate histogram reconstruction on the server side. We also give an extension of PGR, which we call HybridProjectiveGeometryResponse, that allows trading off computation time with utility smoothly.

Differentially Private Clustering via Maximum Coverage

This paper studies the problem of clustering in metric spaces while preserving the privacy of individual data. Specifically, we examine differentially private variants of the k-medians and Euclidean k-means problems. We present polynomial algorithms with constant multiplicative error and lower additive error than the previous state-of-the-art for each problem. Additionally, our algorithms use a clustering algorithm without differential privacy as a black-box. This allows practitioners to control the trade-off between runtime and approximation factor by choosing a suitable clustering algorithm to use.