High Probability Convergence of Stochastic Gradient Methods

In this work, we describe a generic approach to show convergence with high probability for both stochastic convex and non-convex optimization with sub-Gaussian noise. In previous works for convex optimization, either the convergence is only in expectation or the bound depends on the diameter of the domain. Instead, we show high probability convergence with bounds depending on the initial distance to the optimal solution. The algorithms use step sizes analogous to the standard settings and are universal to Lipschitz functions, smooth functions, and their linear combinations. This method can be applied to the non-convex case. We demonstrate an $O((1+\sigma^{2}\log(1/\delta))/T+\sigma/\sqrt{T})$ convergence rate when the number of iterations $T$ is known and an $O((1+\sigma^{2}\log(T/\delta))/\sqrt{T})$ convergence rate when $T$ is unknown for SGD, where $1-\delta$ is the desired success probability. These bounds improve over existing bounds in the literature. Additionally, we demonstrate that our techniques can be used to obtain high probability bound for AdaGrad-Norm (Ward et al., 2019) that removes the bounded gradients assumption from previous works. Furthermore, our technique for AdaGrad-Norm extends to the standard per-coordinate AdaGrad algorithm (Duchi et al., 2011), providing the first noise-adapted high probability convergence for AdaGrad.

META-STORM: Generalized Fully-Adaptive Variance Reduced SGD for Unbounded Functions

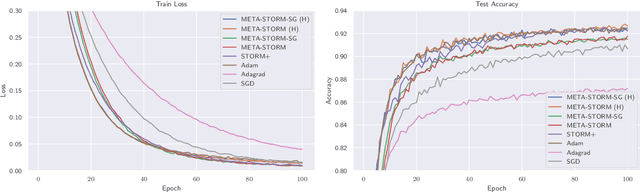
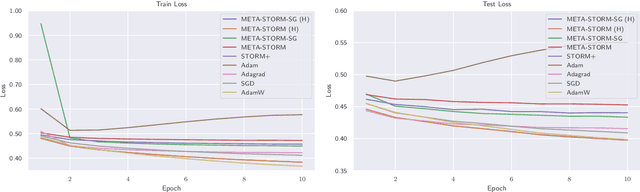
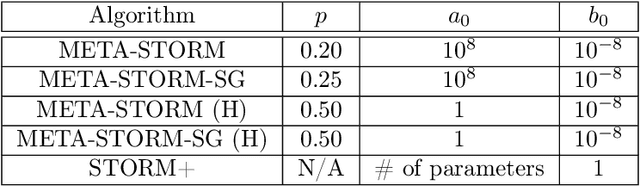
We study the application of variance reduction (VR) techniques to general non-convex stochastic optimization problems. In this setting, the recent work STORM [Cutkosky-Orabona '19] overcomes the drawback of having to compute gradients of "mega-batches" that earlier VR methods rely on. There, STORM utilizes recursive momentum to achieve the VR effect and is then later made fully adaptive in STORM+ [Levy et al., '21], where full-adaptivity removes the requirement for obtaining certain problem-specific parameters such as the smoothness of the objective and bounds on the variance and norm of the stochastic gradients in order to set the step size. However, STORM+ crucially relies on the assumption that the function values are bounded, excluding a large class of useful functions. In this work, we propose META-STORM, a generalized framework of STORM+ that removes this bounded function values assumption while still attaining the optimal convergence rate for non-convex optimization. META-STORM not only maintains full-adaptivity, removing the need to obtain problem specific parameters, but also improves the convergence rate's dependency on the problem parameters. Furthermore, META-STORM can utilize a large range of parameter settings that subsumes previous methods allowing for more flexibility in a wider range of settings. Finally, we demonstrate the effectiveness of META-STORM through experiments across common deep learning tasks. Our algorithm improves upon the previous work STORM+ and is competitive with widely used algorithms after the addition of per-coordinate update and exponential moving average heuristics.

On the Convergence of AdaGrad on $\R^{d}$: Beyond Convexity, Non-Asymptotic Rate and Acceleration

Existing analysis of AdaGrad and other adaptive methods for smooth convex optimization is typically for functions with bounded domain diameter. In unconstrained problems, previous works guarantee an asymptotic convergence rate without an explicit constant factor that holds true for the entire function class. Furthermore, in the stochastic setting, only a modified version of AdaGrad, different from the one commonly used in practice, in which the latest gradient is not used to update the stepsize, has been analyzed. Our paper aims at bridging these gaps and developing a deeper understanding of AdaGrad and its variants in the standard setting of smooth convex functions as well as the more general setting of quasar convex functions. First, we demonstrate new techniques to explicitly bound the convergence rate of the vanilla AdaGrad for unconstrained problems in both deterministic and stochastic settings. Second, we propose a variant of AdaGrad for which we can show the convergence of the last iterate, instead of the average iterate. Finally, we give new accelerated adaptive algorithms and their convergence guarantee in the deterministic setting with explicit dependency on the problem parameters, improving upon the asymptotic rate shown in previous works.

Adaptive Accelerated (Extra-)Gradient Methods with Variance Reduction

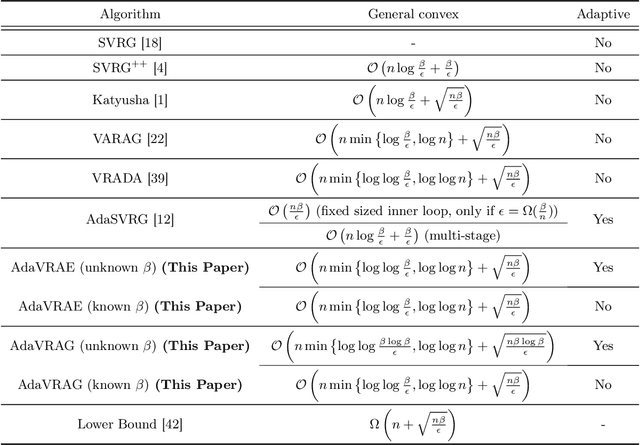
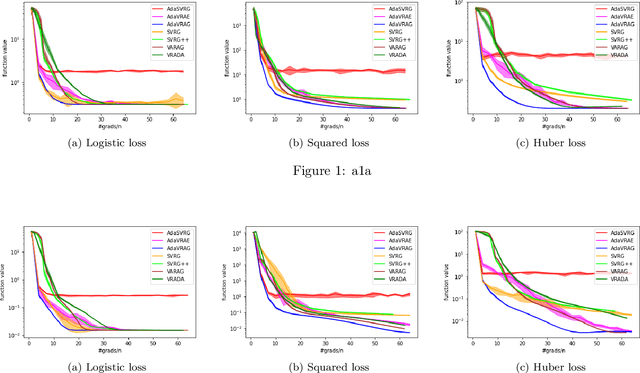
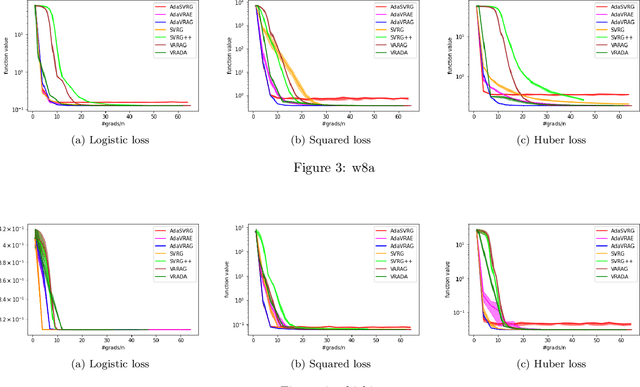
In this paper, we study the finite-sum convex optimization problem focusing on the general convex case. Recently, the study of variance reduced (VR) methods and their accelerated variants has made exciting progress. However, the step size used in the existing VR algorithms typically depends on the smoothness parameter, which is often unknown and requires tuning in practice. To address this problem, we propose two novel adaptive VR algorithms: Adaptive Variance Reduced Accelerated Extra-Gradient (AdaVRAE) and Adaptive Variance Reduced Accelerated Gradient (AdaVRAG). Our algorithms do not require knowledge of the smoothness parameter. AdaVRAE uses $\mathcal{O}\left(n\log\log n+\sqrt{\frac{n\beta}{\epsilon}}\right)$ gradient evaluations and AdaVRAG uses $\mathcal{O}\left(n\log\log n+\sqrt{\frac{n\beta\log\beta}{\epsilon}}\right)$ gradient evaluations to attain an $\mathcal{O}(\epsilon)$-suboptimal solution, where $n$ is the number of functions in the finite sum and $\beta$ is the smoothness parameter. This result matches the best-known convergence rate of non-adaptive VR methods and it improves upon the convergence of the state of the art adaptive VR method, AdaSVRG. We demonstrate the superior performance of our algorithms compared with previous methods in experiments on real-world datasets.

On Adversarial Bias and the Robustness of Fair Machine Learning

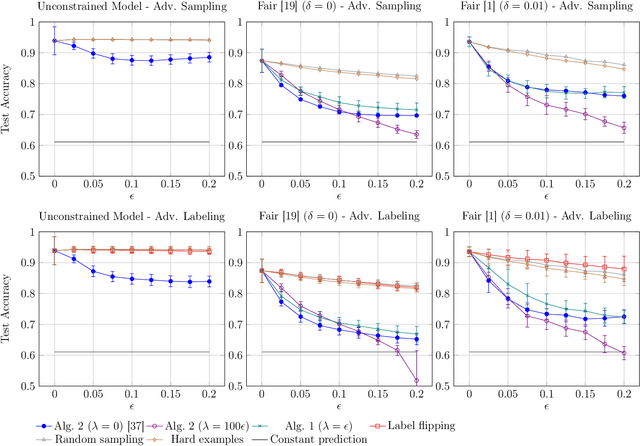
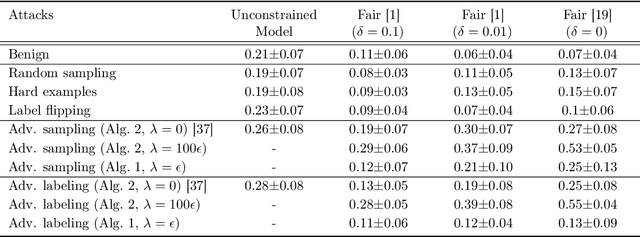
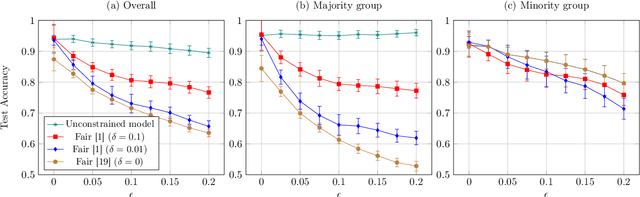
Optimizing prediction accuracy can come at the expense of fairness. Towards minimizing discrimination against a group, fair machine learning algorithms strive to equalize the behavior of a model across different groups, by imposing a fairness constraint on models. However, we show that giving the same importance to groups of different sizes and distributions, to counteract the effect of bias in training data, can be in conflict with robustness. We analyze data poisoning attacks against group-based fair machine learning, with the focus on equalized odds. An adversary who can control sampling or labeling for a fraction of training data, can reduce the test accuracy significantly beyond what he can achieve on unconstrained models. Adversarial sampling and adversarial labeling attacks can also worsen the model's fairness gap on test data, even though the model satisfies the fairness constraint on training data. We analyze the robustness of fair machine learning through an empirical evaluation of attacks on multiple algorithms and benchmark datasets.

Fast Genetic Algorithms

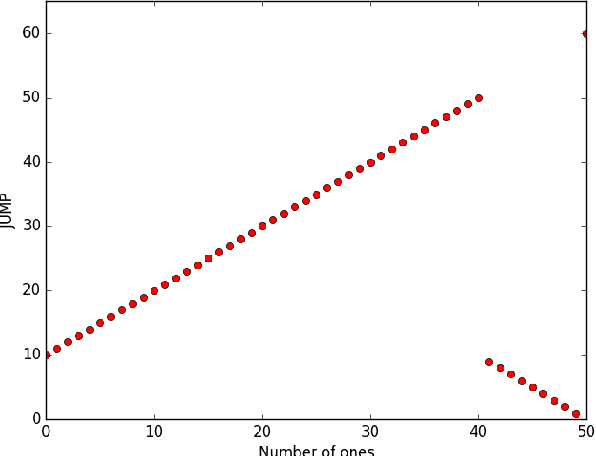
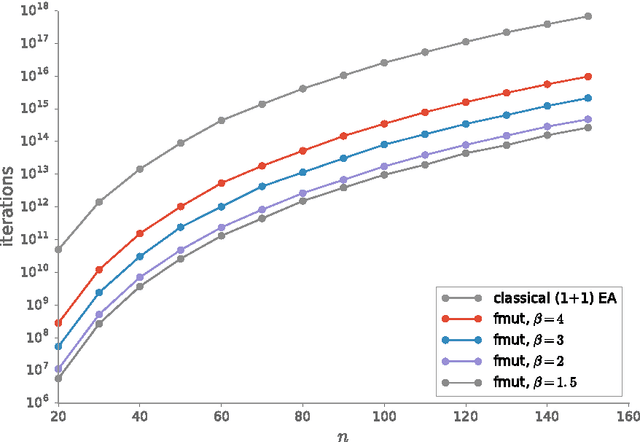
For genetic algorithms using a bit-string representation of length~$n$, the general recommendation is to take $1/n$ as mutation rate. In this work, we discuss whether this is really justified for multimodal functions. Taking jump functions and the $(1+1)$ evolutionary algorithm as the simplest example, we observe that larger mutation rates give significantly better runtimes. For the $\jump_{m,n}$ function, any mutation rate between $2/n$ and $m/n$ leads to a speed-up at least exponential in $m$ compared to the standard choice. The asymptotically best runtime, obtained from using the mutation rate $m/n$ and leading to a speed-up super-exponential in $m$, is very sensitive to small changes of the mutation rate. Any deviation by a small $(1 \pm \eps)$ factor leads to a slow-down exponential in $m$. Consequently, any fixed mutation rate gives strongly sub-optimal results for most jump functions. Building on this observation, we propose to use a random mutation rate $\alpha/n$, where $\alpha$ is chosen from a power-law distribution. We prove that the $(1+1)$ EA with this heavy-tailed mutation rate optimizes any $\jump_{m,n}$ function in a time that is only a small polynomial (in~$m$) factor above the one stemming from the optimal rate for this $m$. Our heavy-tailed mutation operator yields similar speed-ups (over the best known performance guarantees) for the vertex cover problem in bipartite graphs and the matching problem in general graphs. Following the example of fast simulated annealing, fast evolution strategies, and fast evolutionary programming, we propose to call genetic algorithms using a heavy-tailed mutation operator \emph{fast genetic algorithms}.