MarineFormer: A Transformer-based Navigation Policy Model for Collision Avoidance in Marine Environment

In this work, we investigate the problem of Unmanned Surface Vehicle (USV) navigation in a dense marine environment with a high-intensity current flow. The complexities arising from static and dynamic obstacles and the disturbance forces caused by current flow render existing navigation protocols inadequate for ensuring safety and avoiding collisions at sea. To learn a safe and efficient robot policy, we propose a novel methodology that leverages attention mechanisms to capture heterogeneous interactions of the agents with the static and moving obstacles and the flow disturbances from the environment in space and time. In particular, we refine a temporal function with MarineFormer, a Transformer navigation policy for spatially variable Marine environment, trained end-to-end with reinforcement learning (RL). MarineFormer uses foundational spatio-temporal graph attention with transformer architecture to process spatial attention and temporal sequences in an environment that simulates a 2D turbulent marine condition. We propose architectural modifications that improve the stability and learning speed of the recurrent models. The flow velocity estimation, which can be derived from flow simulations or sensors, is incorporated into a model-free RL framework to prevent the robot from entering into high-intensity current flow regions including intense vortices, while potentially leveraging the flow to assist in transportation. The investigated 2D marine environment encompasses flow singularities, including vortices, sinks, and sources, representing fundamental planar flow patterns associated with flood or maritime thunderstorms. Our proposed method is trained with a new reward model to deal with static and dynamic obstacles and disturbances from the current flow.

Complementing Semi-Supervised Learning with Uncertainty Quantification

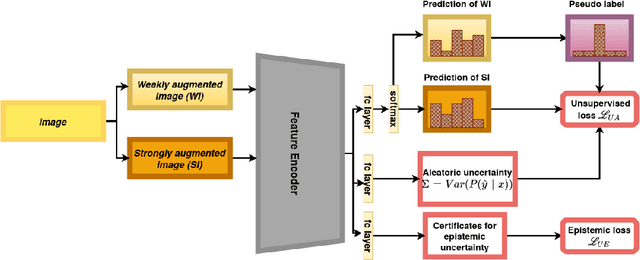
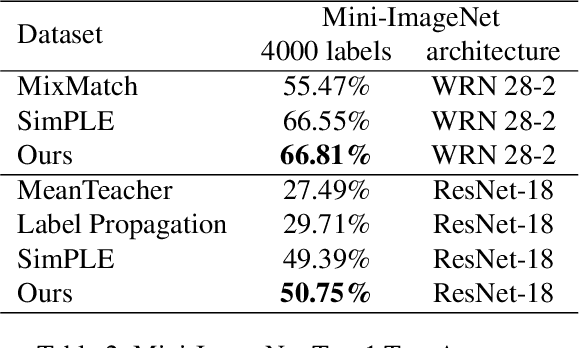
The problem of fully supervised classification is that it requires a tremendous amount of annotated data, however, in many datasets a large portion of data is unlabeled. To alleviate this problem semi-supervised learning (SSL) leverages the knowledge of the classifier on the labeled domain and extrapolates it to the unlabeled domain which has a supposedly similar distribution as annotated data. Recent success on SSL methods crucially hinges on thresholded pseudo labeling and thereby consistency regularization for the unlabeled domain. However, the existing methods do not incorporate the uncertainty of the pseudo labels or unlabeled samples in the training process which are due to the noisy labels or out of distribution samples owing to strong augmentations. Inspired by the recent developments in SSL, our goal in this paper is to propose a novel unsupervised uncertainty-aware objective that relies on aleatoric and epistemic uncertainty quantification. Complementing the recent techniques in SSL with the proposed uncertainty-aware loss function our approach outperforms or is on par with the state-of-the-art over standard SSL benchmarks while being computationally lightweight. Our results outperform the state-of-the-art results on complex datasets such as CIFAR-100 and Mini-ImageNet.

CTIN: Robust Contextual Transformer Network for Inertial Navigation

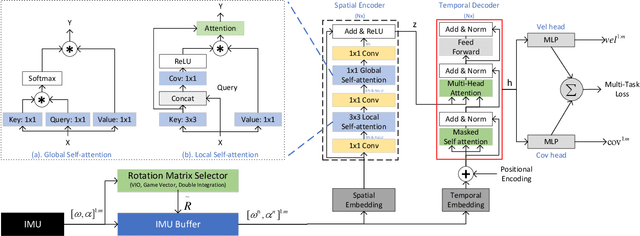
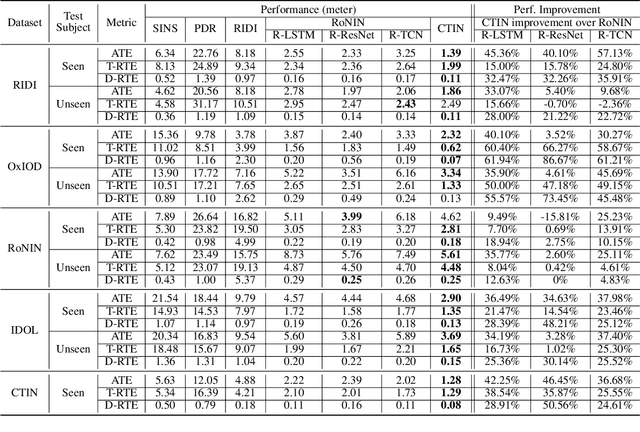
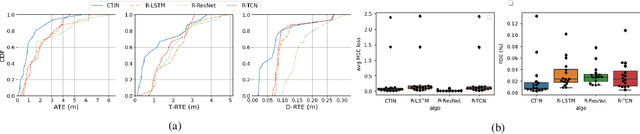
Recently, data-driven inertial navigation approaches have demonstrated their capability of using well-trained neural networks to obtain accurate position estimates from inertial measurement units (IMU) measurements. In this paper, we propose a novel robust Contextual Transformer-based network for Inertial Navigation~(CTIN) to accurately predict velocity and trajectory. To this end, we first design a ResNet-based encoder enhanced by local and global multi-head self-attention to capture spatial contextual information from IMU measurements. Then we fuse these spatial representations with temporal knowledge by leveraging multi-head attention in the Transformer decoder. Finally, multi-task learning with uncertainty reduction is leveraged to improve learning efficiency and prediction accuracy of velocity and trajectory. Through extensive experiments over a wide range of inertial datasets~(e.g. RIDI, OxIOD, RoNIN, IDOL, and our own), CTIN is very robust and outperforms state-of-the-art models.

The Power of Subsampling in Submodular Maximization

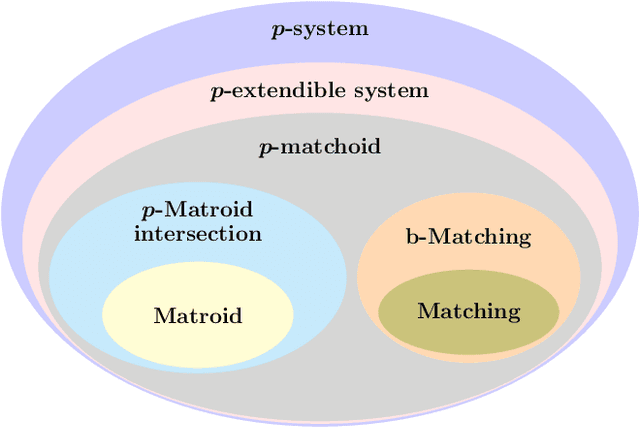
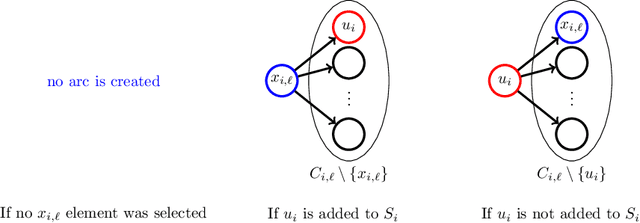
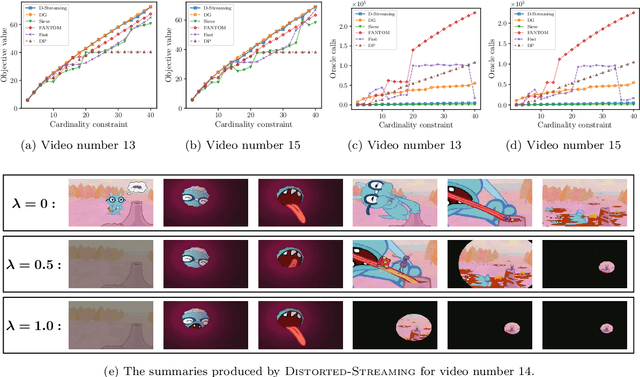
We propose subsampling as a unified algorithmic technique for submodular maximization in centralized and online settings. The idea is simple: independently sample elements from the ground set, and use simple combinatorial techniques (such as greedy or local search) on these sampled elements. We show that this approach leads to optimal/state-of-the-art results despite being much simpler than existing methods. In the usual offline setting, we present SampleGreedy, which obtains a $(p + 2 + o(1))$-approximation for maximizing a submodular function subject to a $p$-extendible system using $O(n + nk/p)$ evaluation and feasibility queries, where $k$ is the size of the largest feasible set. The approximation ratio improves to $p+1$ and $p$ for monotone submodular and linear objectives, respectively. In the streaming setting, we present SampleStreaming, which obtains a $(4p +2 - o(1))$-approximation for maximizing a submodular function subject to a $p$-matchoid using $O(k)$ memory and $O(km/p)$ evaluation and feasibility queries per element, where $m$ is the number of matroids defining the $p$-matchoid. The approximation ratio improves to $4p$ for monotone submodular objectives. We empirically demonstrate the effectiveness of our algorithms on video summarization, location summarization, and movie recommendation tasks.

Generating Structured Adversarial Attacks Using Frank-Wolfe Method

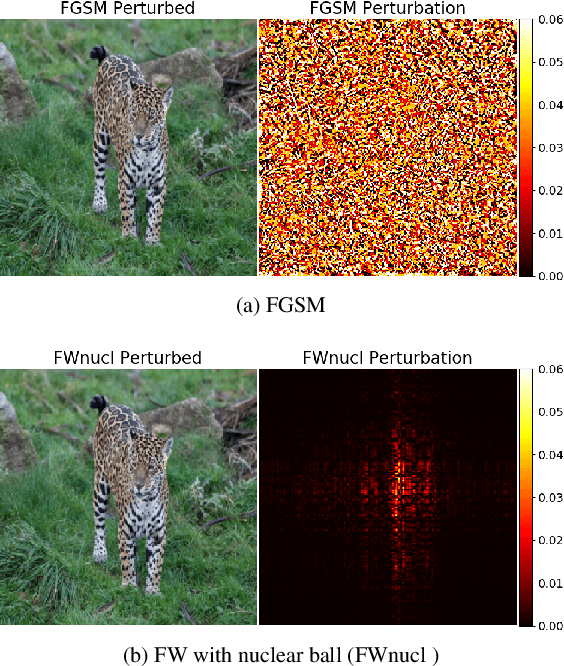
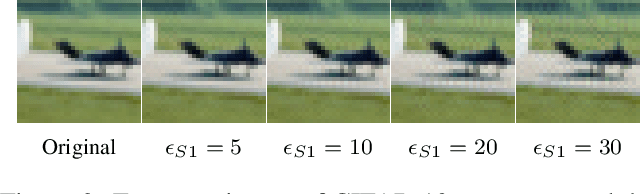
White box adversarial perturbations are generated via iterative optimization algorithms most often by minimizing an adversarial loss on a $\ell_p$ neighborhood of the original image, the so-called distortion set. Constraining the adversarial search with different norms results in disparately structured adversarial examples. Here we explore several distortion sets with structure-enhancing algorithms. These new structures for adversarial examples might provide challenges for provable and empirical robust mechanisms. Because adversarial robustness is still an empirical field, defense mechanisms should also reasonably be evaluated against differently structured attacks. Besides, these structured adversarial perturbations may allow for larger distortions size than their $\ell_p$ counter-part while remaining imperceptible or perceptible as natural distortions of the image. We will demonstrate in this work that the proposed structured adversarial examples can significantly bring down the classification accuracy of adversarialy trained classifiers while showing low $\ell_2$ distortion rate. For instance, on ImagNet dataset the structured attacks drop the accuracy of adversarial model to near zero with only 50\% of $\ell_2$ distortion generated using white-box attacks like PGD. As a byproduct, our finding on structured adversarial examples can be used for adversarial regularization of models to make models more robust or improve their generalization performance on datasets which are structurally different.

Trace-Norm Adversarial Examples

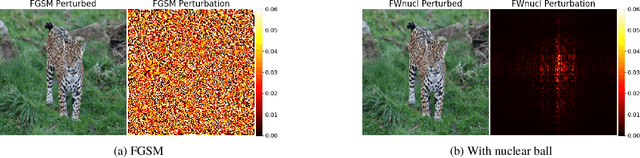
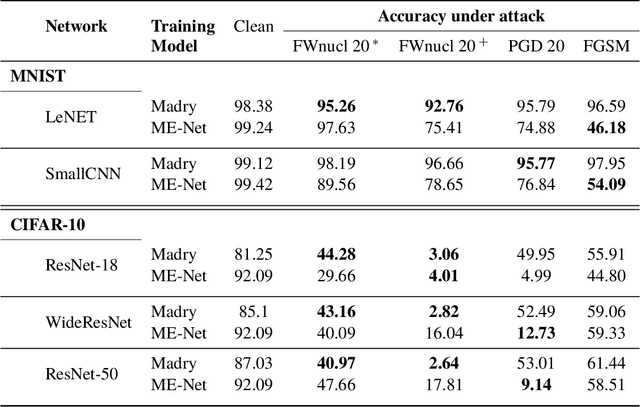
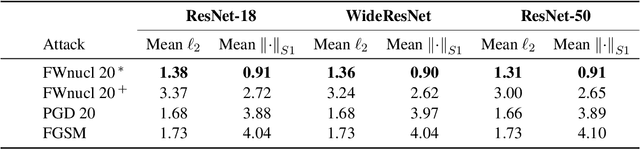
White box adversarial perturbations are sought via iterative optimization algorithms most often minimizing an adversarial loss on a $l_p$ neighborhood of the original image, the so-called distortion set. Constraining the adversarial search with different norms results in disparately structured adversarial examples. Here we explore several distortion sets with structure-enhancing algorithms. These new structures for adversarial examples, yet pervasive in optimization, are for instance a challenge for adversarial theoretical certification which again provides only $l_p$ certificates. Because adversarial robustness is still an empirical field, defense mechanisms should also reasonably be evaluated against differently structured attacks. Besides, these structured adversarial perturbations may allow for larger distortions size than their $l_p$ counter-part while remaining imperceptible or perceptible as natural slight distortions of the image. Finally, they allow some control on the generation of the adversarial perturbation, like (localized) bluriness.

On Adversarial Bias and the Robustness of Fair Machine Learning

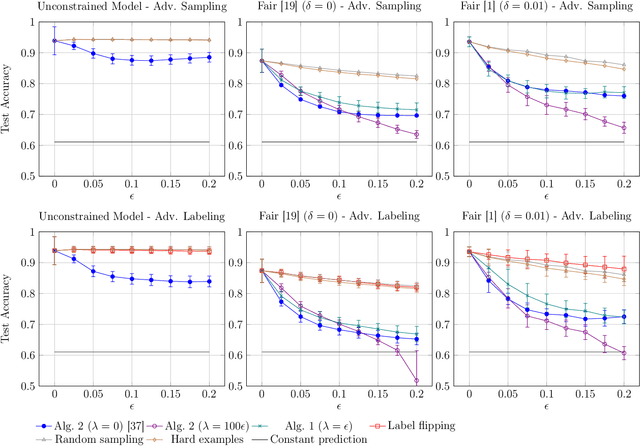
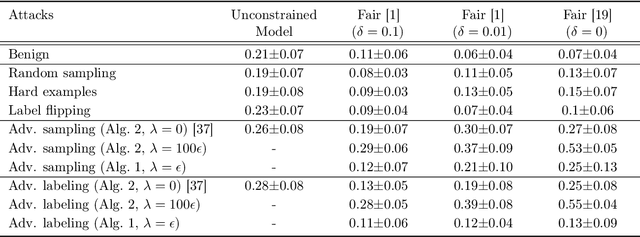
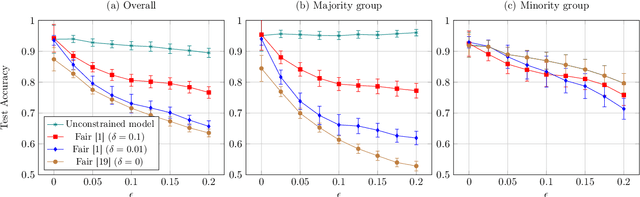
Optimizing prediction accuracy can come at the expense of fairness. Towards minimizing discrimination against a group, fair machine learning algorithms strive to equalize the behavior of a model across different groups, by imposing a fairness constraint on models. However, we show that giving the same importance to groups of different sizes and distributions, to counteract the effect of bias in training data, can be in conflict with robustness. We analyze data poisoning attacks against group-based fair machine learning, with the focus on equalized odds. An adversary who can control sampling or labeling for a fraction of training data, can reduce the test accuracy significantly beyond what he can achieve on unconstrained models. Adversarial sampling and adversarial labeling attacks can also worsen the model's fairness gap on test data, even though the model satisfies the fairness constraint on training data. We analyze the robustness of fair machine learning through an empirical evaluation of attacks on multiple algorithms and benchmark datasets.

Submodular Maximization Through Barrier Functions

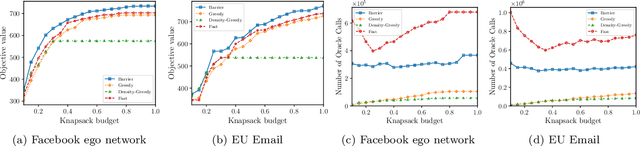
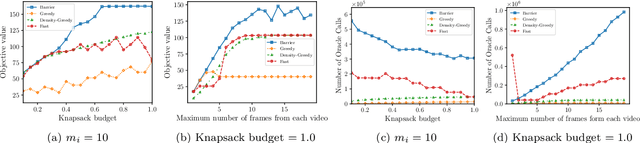
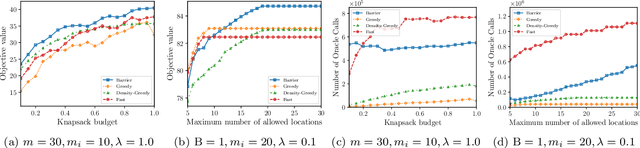
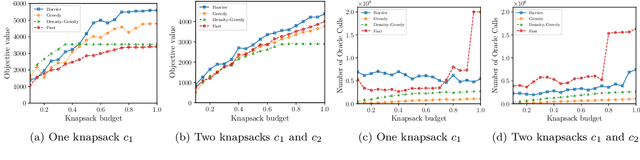
In this paper, we introduce a novel technique for constrained submodular maximization, inspired by barrier functions in continuous optimization. This connection not only improves the running time for constrained submodular maximization but also provides the state of the art guarantee. More precisely, for maximizing a monotone submodular function subject to the combination of a $k$-matchoid and $\ell$-knapsack constraint (for $\ell\leq k$), we propose a potential function that can be approximately minimized. Once we minimize the potential function up to an $\epsilon$ error it is guaranteed that we have found a feasible set with a $2(k+1+\epsilon)$-approximation factor which can indeed be further improved to $(k+1+\epsilon)$ by an enumeration technique. We extensively evaluate the performance of our proposed algorithm over several real-world applications, including a movie recommendation system, summarization tasks for YouTube videos, Twitter feeds and Yelp business locations, and a set cover problem.

Regularized Submodular Maximization at Scale

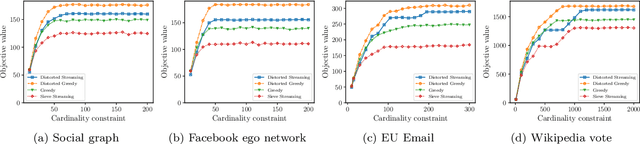
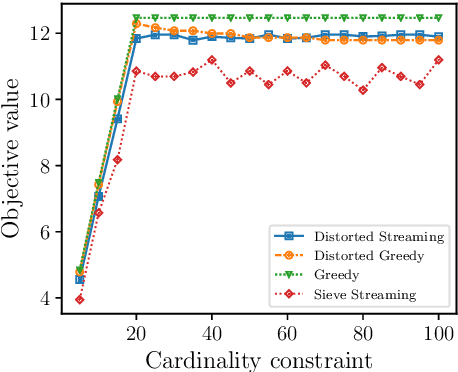
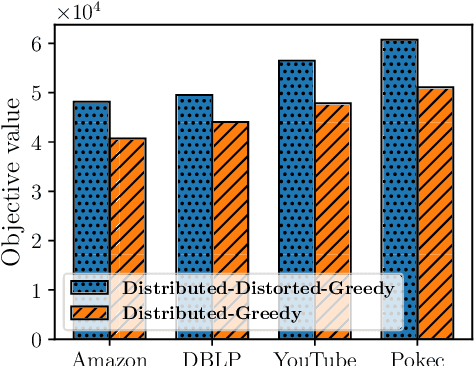
In this paper, we propose scalable methods for maximizing a regularized submodular function $f = g - \ell$ expressed as the difference between a monotone submodular function $g$ and a modular function $\ell$. Indeed, submodularity is inherently related to the notions of diversity, coverage, and representativeness. In particular, finding the mode of many popular probabilistic models of diversity, such as determinantal point processes, submodular probabilistic models, and strongly log-concave distributions, involves maximization of (regularized) submodular functions. Since a regularized function $f$ can potentially take on negative values, the classic theory of submodular maximization, which heavily relies on the non-negativity assumption of submodular functions, may not be applicable. To circumvent this challenge, we develop the first one-pass streaming algorithm for maximizing a regularized submodular function subject to a $k$-cardinality constraint. It returns a solution $S$ with the guarantee that $f(S)\geq(\phi^{-2}-\epsilon) \cdot g(OPT)-\ell (OPT)$, where $\phi$ is the golden ratio. Furthermore, we develop the first distributed algorithm that returns a solution $S$ with the guarantee that $\mathbb{E}[f(S)] \geq (1-\epsilon) [(1-e^{-1}) \cdot g(OPT)-\ell(OPT)]$ in $O(1/ \epsilon)$ rounds of MapReduce computation, without keeping multiple copies of the entire dataset in each round (as it is usually done). We should highlight that our result, even for the unregularized case where the modular term $\ell$ is zero, improves the memory and communication complexity of the existing work by a factor of $O(1/ \epsilon)$ while arguably provides a simpler distributed algorithm and a unifying analysis. We also empirically study the performance of our scalable methods on a set of real-life applications, including finding the mode of distributions, data summarization, and product recommendation.

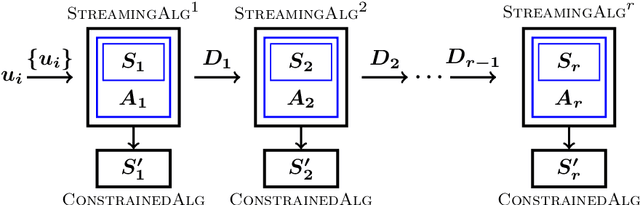
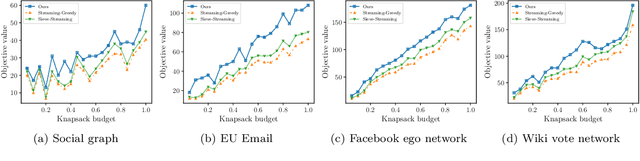
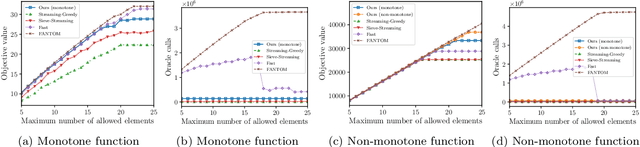
Streaming Submodular Maximization under a $k$-Set System Constraint

In this paper, we propose a novel framework that converts streaming algorithms for monotone submodular maximization into streaming algorithms for non-monotone submodular maximization. This reduction readily leads to the currently tightest deterministic approximation ratio for submodular maximization subject to a $k$-matchoid constraint. Moreover, we propose the first streaming algorithm for monotone submodular maximization subject to $k$-extendible and $k$-set system constraints. Together with our proposed reduction, we obtain $O(k\log k)$ and $O(k^2\log k)$ approximation ratio for submodular maximization subject to the above constraints, respectively. We extensively evaluate the empirical performance of our algorithm against the existing work in a series of experiments including finding the maximum independent set in randomly generated graphs, maximizing linear functions over social networks, movie recommendation, Yelp location summarization, and Twitter data summarization.