The Power of Subsampling in Submodular Maximization
Paper and Code
Apr 06, 2021
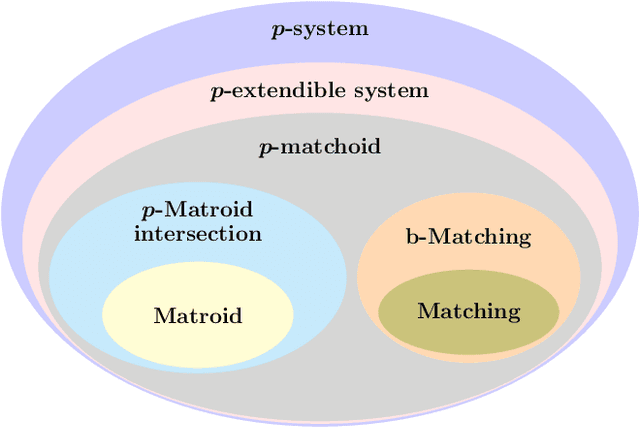

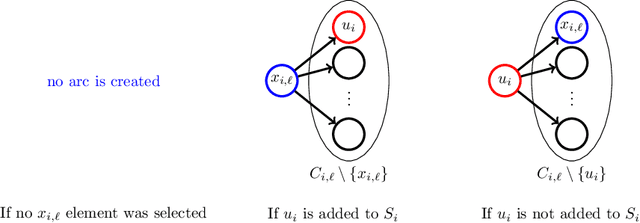
We propose subsampling as a unified algorithmic technique for submodular maximization in centralized and online settings. The idea is simple: independently sample elements from the ground set, and use simple combinatorial techniques (such as greedy or local search) on these sampled elements. We show that this approach leads to optimal/state-of-the-art results despite being much simpler than existing methods. In the usual offline setting, we present SampleGreedy, which obtains a $(p + 2 + o(1))$-approximation for maximizing a submodular function subject to a $p$-extendible system using $O(n + nk/p)$ evaluation and feasibility queries, where $k$ is the size of the largest feasible set. The approximation ratio improves to $p+1$ and $p$ for monotone submodular and linear objectives, respectively. In the streaming setting, we present SampleStreaming, which obtains a $(4p +2 - o(1))$-approximation for maximizing a submodular function subject to a $p$-matchoid using $O(k)$ memory and $O(km/p)$ evaluation and feasibility queries per element, where $m$ is the number of matroids defining the $p$-matchoid. The approximation ratio improves to $4p$ for monotone submodular objectives. We empirically demonstrate the effectiveness of our algorithms on video summarization, location summarization, and movie recommendation tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge