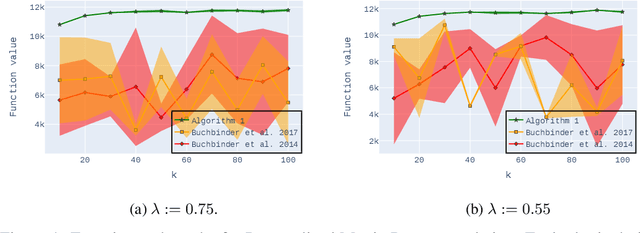
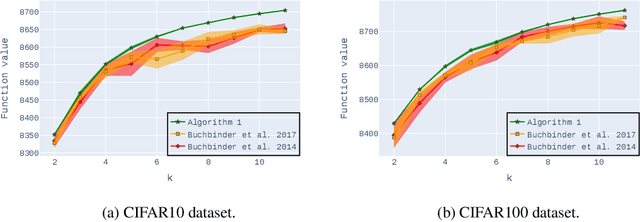
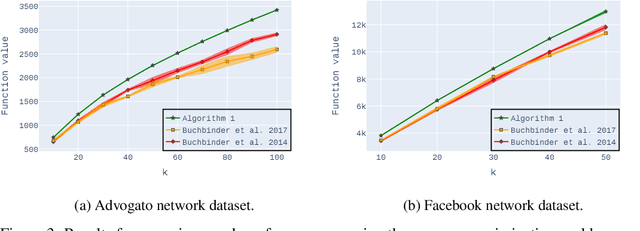
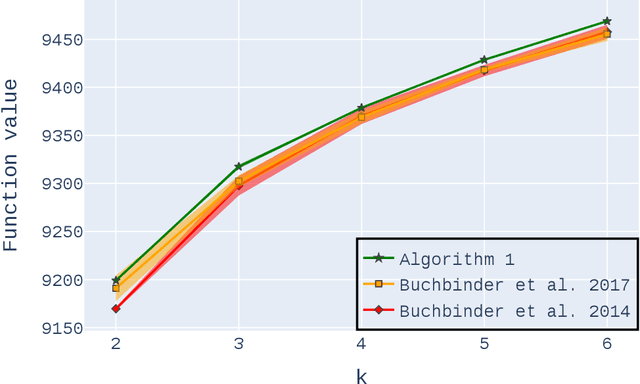
Practical $0.385$-Approximation for Submodular Maximization Subject to a Cardinality Constraint

Non-monotone constrained submodular maximization plays a crucial role in various machine learning applications. However, existing algorithms often struggle with a trade-off between approximation guarantees and practical efficiency. The current state-of-the-art is a recent $0.401$-approximation algorithm, but its computational complexity makes it highly impractical. The best practical algorithms for the problem only guarantee $1/e$-approximation. In this work, we present a novel algorithm for submodular maximization subject to a cardinality constraint that combines a guarantee of $0.385$-approximation with a low and practical query complexity of $O(n+k^2)$. Furthermore, we evaluate the empirical performance of our algorithm in experiments based on various machine learning applications, including Movie Recommendation, Image Summarization, and more. These experiments demonstrate the efficacy of our approach.

Submodular Minimax Optimization: Finding Effective Sets

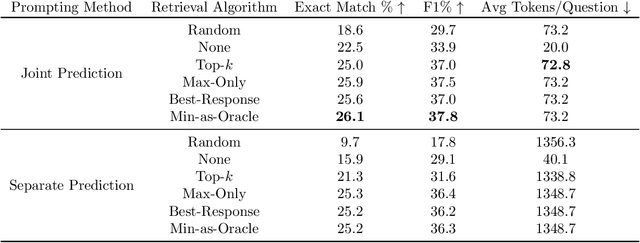
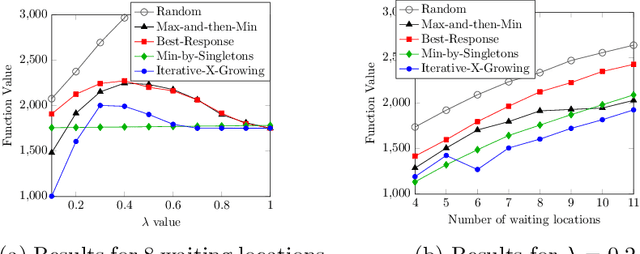
Despite the rich existing literature about minimax optimization in continuous settings, only very partial results of this kind have been obtained for combinatorial settings. In this paper, we fill this gap by providing a characterization of submodular minimax optimization, the problem of finding a set (for either the min or the max player) that is effective against every possible response. We show when and under what conditions we can find such sets. We also demonstrate how minimax submodular optimization provides robust solutions for downstream machine learning applications such as (i) efficient prompt engineering for question answering, (ii) prompt engineering for dialog state tracking, (iii) identifying robust waiting locations for ride-sharing, (iv) ride-share difficulty kernelization, and (v) finding adversarial images. Our experiments demonstrate that our proposed algorithms consistently outperform other baselines.

Resolving the Approximability of Offline and Online Non-monotone DR-Submodular Maximization over General Convex Sets

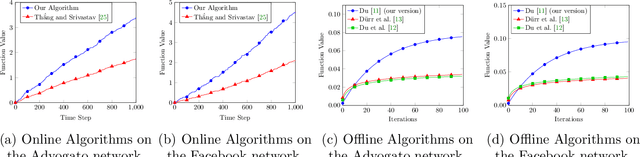
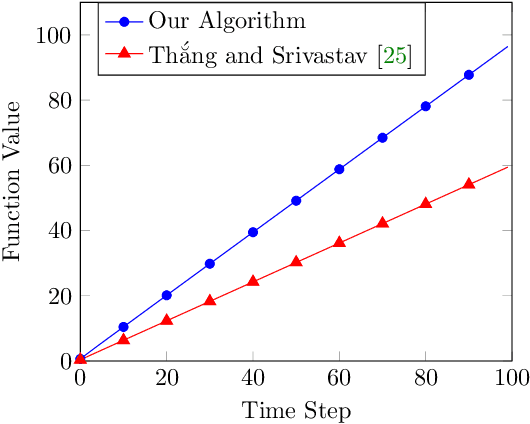
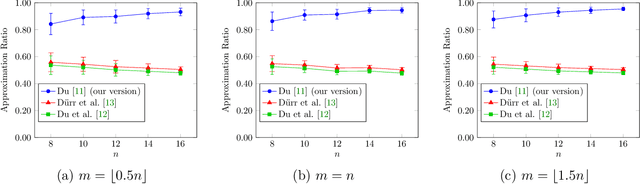
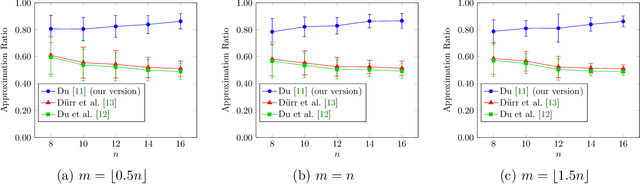
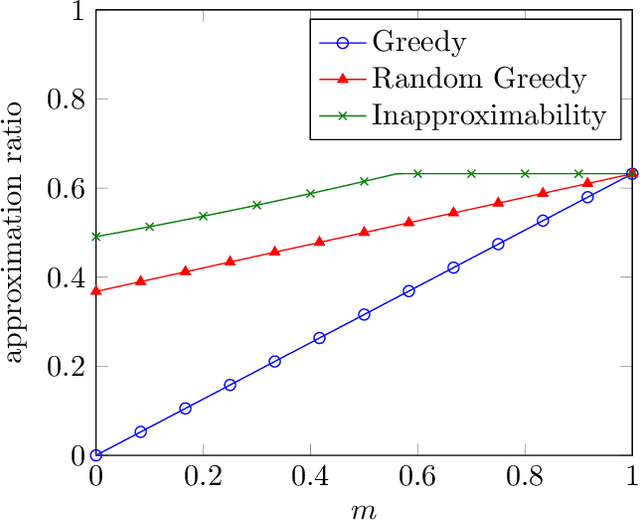
In recent years, maximization of DR-submodular continuous functions became an important research field, with many real-worlds applications in the domains of machine learning, communication systems, operation research and economics. Most of the works in this field study maximization subject to down-closed convex set constraints due to an inapproximability result by Vondr\'ak (2013). However, Durr et al. (2021) showed that one can bypass this inapproximability by proving approximation ratios that are functions of $m$, the minimum $\ell_{\infty}$-norm of any feasible vector. Given this observation, it is possible to get results for maximizing a DR-submodular function subject to general convex set constraints, which has led to multiple works on this problem. The most recent of which is a polynomial time $\tfrac{1}{4}(1 - m)$-approximation offline algorithm due to Du (2022). However, only a sub-exponential time $\tfrac{1}{3\sqrt{3}}(1 - m)$-approximation algorithm is known for the corresponding online problem. In this work, we present a polynomial time online algorithm matching the $\tfrac{1}{4}(1 - m)$-approximation of the state-of-the-art offline algorithm. We also present an inapproximability result showing that our online algorithm and Du's (2022) offline algorithm are both optimal in a strong sense. Finally, we study the empirical performance of our algorithm and the algorithm of Du (which was only theoretically studied previously), and show that they consistently outperform previously suggested algorithms on revenue maximization, location summarization and quadratic programming applications.

Using Partial Monotonicity in Submodular Maximization

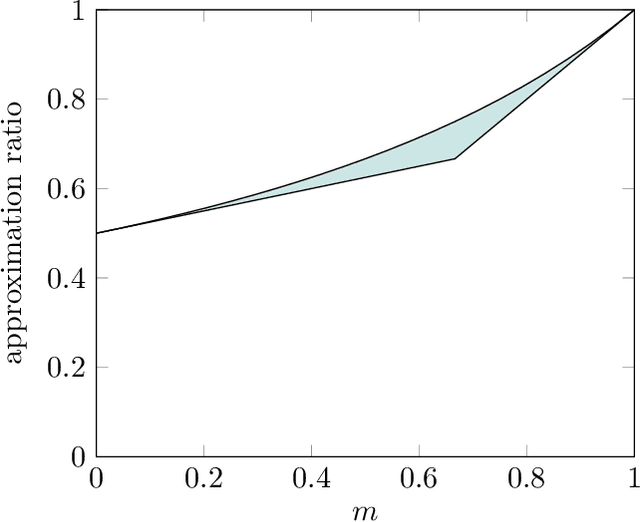
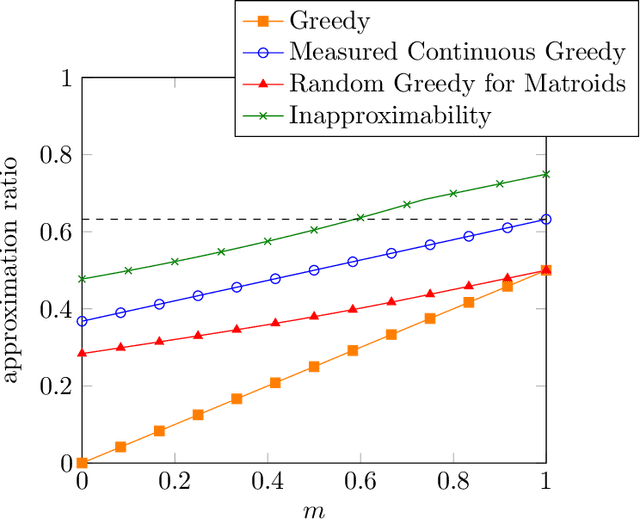
Over the last two decades, submodular function maximization has been the workhorse of many discrete optimization problems in machine learning applications. Traditionally, the study of submodular functions was based on binary function properties. However, such properties have an inherit weakness, namely, if an algorithm assumes functions that have a particular property, then it provides no guarantee for functions that violate this property, even when the violation is very slight. Therefore, recent works began to consider continuous versions of function properties. Probably the most significant among these (so far) are the submodularity ratio and the curvature, which were studied extensively together and separately. The monotonicity property of set functions plays a central role in submodular maximization. Nevertheless, and despite all the above works, no continuous version of this property has been suggested to date (as far as we know). This is unfortunate since submoduar functions that are almost monotone often arise in machine learning applications. In this work we fill this gap by defining the monotonicity ratio, which is a continues version of the monotonicity property. We then show that for many standard submodular maximization algorithms one can prove new approximation guarantees that depend on the monotonicity ratio; leading to improved approximation ratios for the common machine learning applications of movie recommendation, quadratic programming and image summarization.

Submodular + Concave

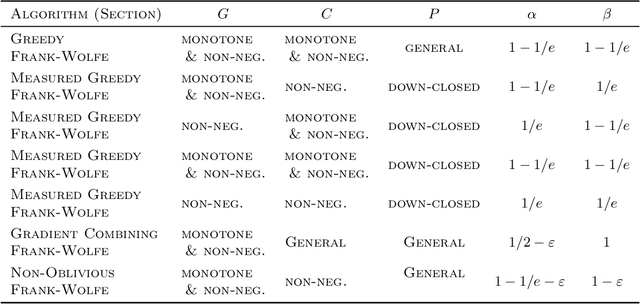
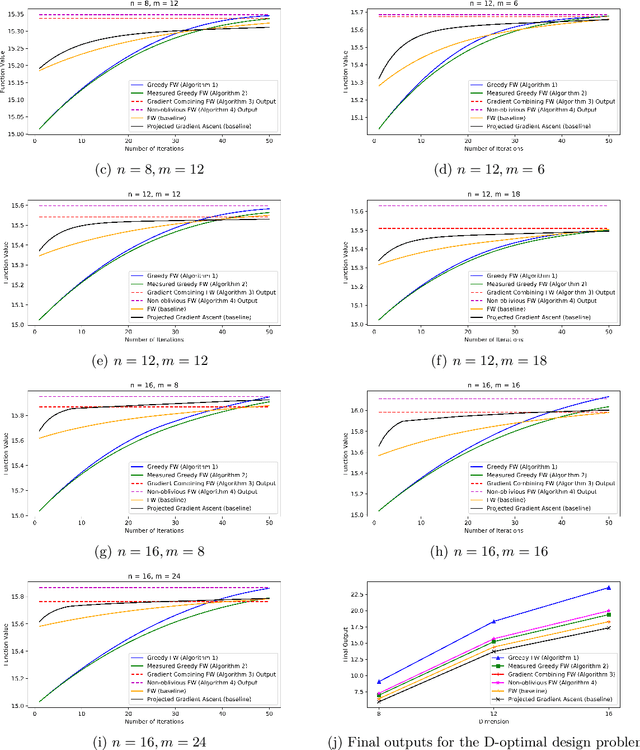
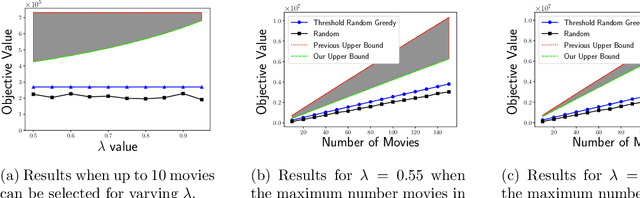
It has been well established that first order optimization methods can converge to the maximal objective value of concave functions and provide constant factor approximation guarantees for (non-convex/non-concave) continuous submodular functions. In this work, we initiate the study of the maximization of functions of the form $F(x) = G(x) +C(x)$ over a solvable convex body $P$, where $G$ is a smooth DR-submodular function and $C$ is a smooth concave function. This class of functions is a strict extension of both concave and continuous DR-submodular functions for which no theoretical guarantee is known. We provide a suite of Frank-Wolfe style algorithms, which, depending on the nature of the objective function (i.e., if $G$ and $C$ are monotone or not, and non-negative or not) and on the nature of the set $P$ (i.e., whether it is downward closed or not), provide $1-1/e$, $1/e$, or $1/2$ approximation guarantees. We then use our algorithms to get a framework to smoothly interpolate between choosing a diverse set of elements from a given ground set (corresponding to the mode of a determinantal point process) and choosing a clustered set of elements (corresponding to the maxima of a suitable concave function). Additionally, we apply our algorithms to various functions in the above class (DR-submodular + concave) in both constrained and unconstrained settings, and show that our algorithms consistently outperform natural baselines.

The Power of Subsampling in Submodular Maximization

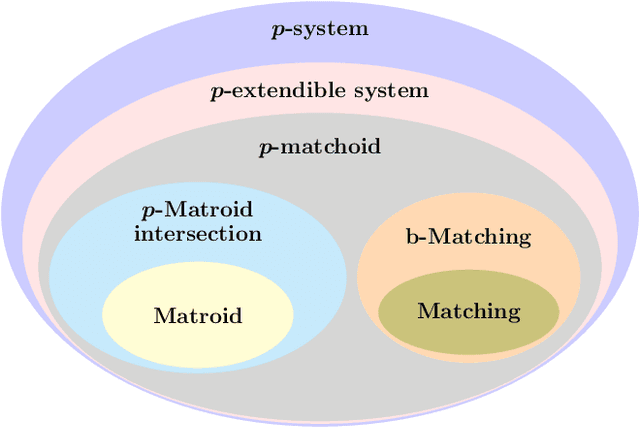
We propose subsampling as a unified algorithmic technique for submodular maximization in centralized and online settings. The idea is simple: independently sample elements from the ground set, and use simple combinatorial techniques (such as greedy or local search) on these sampled elements. We show that this approach leads to optimal/state-of-the-art results despite being much simpler than existing methods. In the usual offline setting, we present SampleGreedy, which obtains a $(p + 2 + o(1))$-approximation for maximizing a submodular function subject to a $p$-extendible system using $O(n + nk/p)$ evaluation and feasibility queries, where $k$ is the size of the largest feasible set. The approximation ratio improves to $p+1$ and $p$ for monotone submodular and linear objectives, respectively. In the streaming setting, we present SampleStreaming, which obtains a $(4p +2 - o(1))$-approximation for maximizing a submodular function subject to a $p$-matchoid using $O(k)$ memory and $O(km/p)$ evaluation and feasibility queries per element, where $m$ is the number of matroids defining the $p$-matchoid. The approximation ratio improves to $4p$ for monotone submodular objectives. We empirically demonstrate the effectiveness of our algorithms on video summarization, location summarization, and movie recommendation tasks.

Simultaneous Greedys: A Swiss Army Knife for Constrained Submodular Maximization

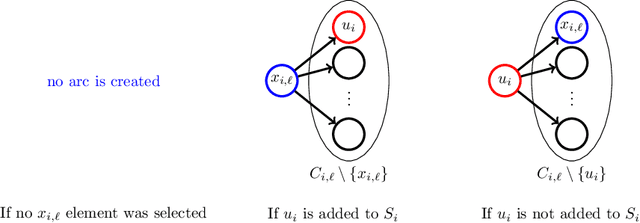
In this paper, we present SimultaneousGreedys, a deterministic algorithm for constrained submodular maximization. At a high level, the algorithm maintains $\ell$ solutions and greedily updates them in a simultaneous fashion, rather than a sequential one. SimultaneousGreedys achieves the tightest known approximation guarantees for both $k$-extendible systems and the more general $k$-systems, which are $(k+1)^2/k = k + \mathcal{O}(1)$ and $(1 + \sqrt{k+2})^2 = k + \mathcal{O}(\sqrt{k})$, respectively. This is in contrast to previous algorithms, which are designed to provide tight approximation guarantees in one setting, but not both. Furthermore, these approximation guarantees further improve to $k+1$ when the objective is monotone. We demonstrate that the algorithm may be modified to run in nearly linear time with an arbitrarily small loss in the approximation. This leads to the first nearly linear time algorithm for submodular maximization over $k$-extendible systems and $k$-systems. Finally, the technique is flexible enough to incorporate the intersection of $m$ additional knapsack constraints, while retaining similar approximation guarantees, which are roughly $k + 2m + \mathcal{O}(\sqrt{k+m})$ for $k$-systems and $k+2m + \mathcal{O}(\sqrt{m})$ for $k$-extendible systems. To complement our algorithmic contributions, we provide a hardness result which states that no algorithm making polynomially many queries to the value and independence oracles can achieve an approximation better than $k + 1/2 + \varepsilon$.

Continuous Submodular Maximization: Beyond DR-Submodularity

In this paper, we propose the first continuous optimization algorithms that achieve a constant factor approximation guarantee for the problem of monotone continuous submodular maximization subject to a linear constraint. We first prove that a simple variant of the vanilla coordinate ascent, called Coordinate-Ascent+, achieves a $(\frac{e-1}{2e-1}-\varepsilon)$-approximation guarantee while performing $O(n/\varepsilon)$ iterations, where the computational complexity of each iteration is roughly $O(n/\sqrt{\varepsilon}+n\log n)$ (here, $n$ denotes the dimension of the optimization problem). We then propose Coordinate-Ascent++, that achieves the tight $(1-1/e-\varepsilon)$-approximation guarantee while performing the same number of iterations, but at a higher computational complexity of roughly $O(n^3/\varepsilon^{2.5} + n^3 \log n / \varepsilon^2)$ per iteration. However, the computation of each round of Coordinate-Ascent++ can be easily parallelized so that the computational cost per machine scales as $O(n/\sqrt{\varepsilon}+n\log n)$.

Regularized Submodular Maximization at Scale

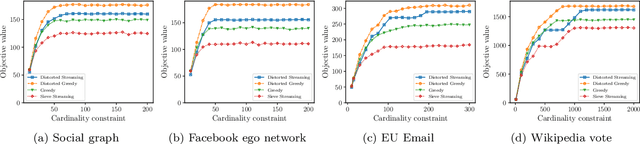
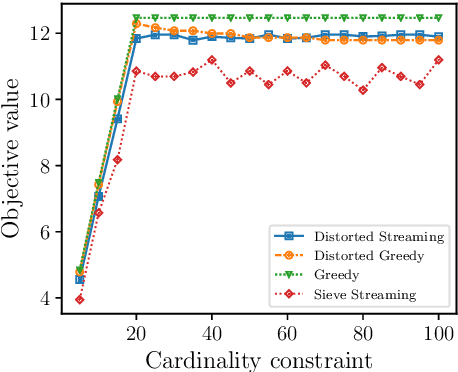
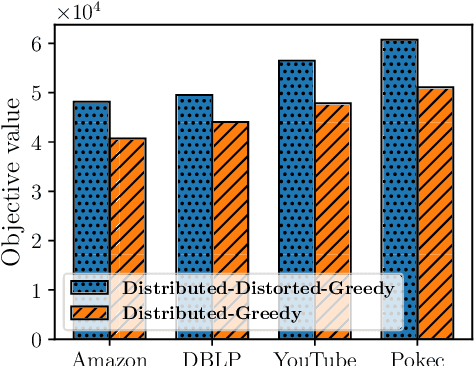
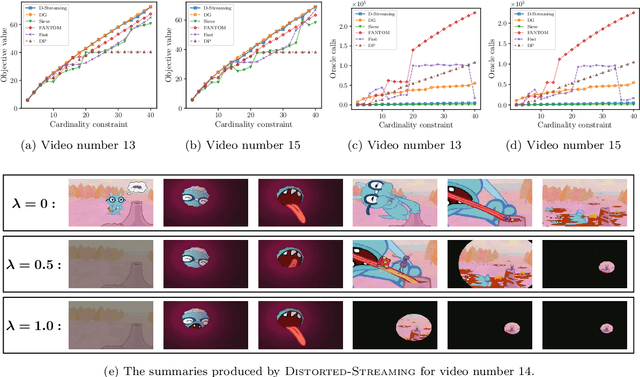
In this paper, we propose scalable methods for maximizing a regularized submodular function $f = g - \ell$ expressed as the difference between a monotone submodular function $g$ and a modular function $\ell$. Indeed, submodularity is inherently related to the notions of diversity, coverage, and representativeness. In particular, finding the mode of many popular probabilistic models of diversity, such as determinantal point processes, submodular probabilistic models, and strongly log-concave distributions, involves maximization of (regularized) submodular functions. Since a regularized function $f$ can potentially take on negative values, the classic theory of submodular maximization, which heavily relies on the non-negativity assumption of submodular functions, may not be applicable. To circumvent this challenge, we develop the first one-pass streaming algorithm for maximizing a regularized submodular function subject to a $k$-cardinality constraint. It returns a solution $S$ with the guarantee that $f(S)\geq(\phi^{-2}-\epsilon) \cdot g(OPT)-\ell (OPT)$, where $\phi$ is the golden ratio. Furthermore, we develop the first distributed algorithm that returns a solution $S$ with the guarantee that $\mathbb{E}[f(S)] \geq (1-\epsilon) [(1-e^{-1}) \cdot g(OPT)-\ell(OPT)]$ in $O(1/ \epsilon)$ rounds of MapReduce computation, without keeping multiple copies of the entire dataset in each round (as it is usually done). We should highlight that our result, even for the unregularized case where the modular term $\ell$ is zero, improves the memory and communication complexity of the existing work by a factor of $O(1/ \epsilon)$ while arguably provides a simpler distributed algorithm and a unifying analysis. We also empirically study the performance of our scalable methods on a set of real-life applications, including finding the mode of distributions, data summarization, and product recommendation.

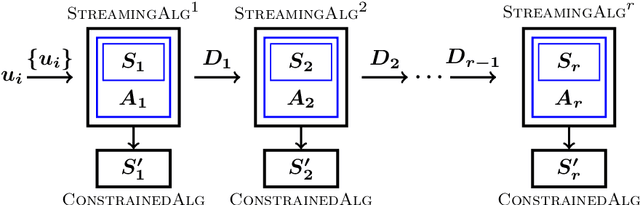
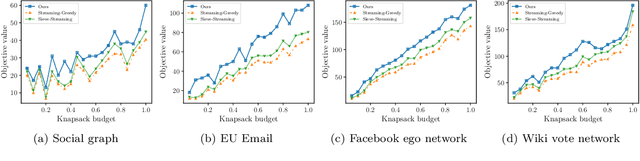
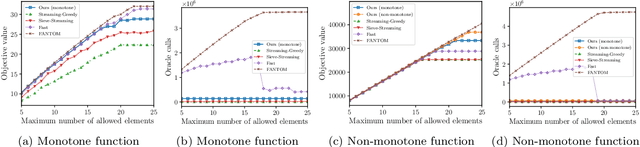
Streaming Submodular Maximization under a $k$-Set System Constraint

In this paper, we propose a novel framework that converts streaming algorithms for monotone submodular maximization into streaming algorithms for non-monotone submodular maximization. This reduction readily leads to the currently tightest deterministic approximation ratio for submodular maximization subject to a $k$-matchoid constraint. Moreover, we propose the first streaming algorithm for monotone submodular maximization subject to $k$-extendible and $k$-set system constraints. Together with our proposed reduction, we obtain $O(k\log k)$ and $O(k^2\log k)$ approximation ratio for submodular maximization subject to the above constraints, respectively. We extensively evaluate the empirical performance of our algorithm against the existing work in a series of experiments including finding the maximum independent set in randomly generated graphs, maximizing linear functions over social networks, movie recommendation, Yelp location summarization, and Twitter data summarization.