Fast Convergence of $Φ$-Divergence Along the Unadjusted Langevin Algorithm and Proximal Sampler

We study the mixing time of two popular discrete time Markov chains in continuous space, the unadjusted Langevin algorithm and the proximal sampler, which are discretizations of the Langevin dynamics. We extend mixing time analyses for these Markov chains to hold in $\Phi$-divergence. We show that any $\Phi$-divergence arising from a twice-differentiable strictly convex function $\Phi$ converges to $0$ exponentially fast along these Markov chains, under the assumption that their stationary distributions satisfies the corresponding $\Phi$-Sobolev inequality. Our rates of convergence are tight and include as special cases popular mixing time regimes, namely the mixing in chi-squared divergence under a Poincar\'e inequality, and the mixing in relative entropy under a log-Sobolev inequality. Our results follow by bounding the contraction coefficients arising in the appropriate strong data processing inequalities.

On Independent Samples Along the Langevin Diffusion and the Unadjusted Langevin Algorithm

We study the rate at which the initial and current random variables become independent along a Markov chain, focusing on the Langevin diffusion in continuous time and the Unadjusted Langevin Algorithm (ULA) in discrete time. We measure the dependence between random variables via their mutual information. For the Langevin diffusion, we show the mutual information converges to $0$ exponentially fast when the target is strongly log-concave, and at a polynomial rate when the target is weakly log-concave. These rates are analogous to the mixing time of the Langevin diffusion under similar assumptions. For the ULA, we show the mutual information converges to $0$ exponentially fast when the target is strongly log-concave and smooth. We prove our results by developing the mutual version of the mixing time analyses of these Markov chains. We also provide alternative proofs based on strong data processing inequalities for the Langevin diffusion and the ULA, and by showing regularity results for these processes in mutual information.

Langevin Thompson Sampling with Logarithmic Communication: Bandits and Reinforcement Learning

Thompson sampling (TS) is widely used in sequential decision making due to its ease of use and appealing empirical performance. However, many existing analytical and empirical results for TS rely on restrictive assumptions on reward distributions, such as belonging to conjugate families, which limits their applicability in realistic scenarios. Moreover, sequential decision making problems are often carried out in a batched manner, either due to the inherent nature of the problem or to serve the purpose of reducing communication and computation costs. In this work, we jointly study these problems in two popular settings, namely, stochastic multi-armed bandits (MABs) and infinite-horizon reinforcement learning (RL), where TS is used to learn the unknown reward distributions and transition dynamics, respectively. We propose batched $\textit{Langevin Thompson Sampling}$ algorithms that leverage MCMC methods to sample from approximate posteriors with only logarithmic communication costs in terms of batches. Our algorithms are computationally efficient and maintain the same order-optimal regret guarantees of $\mathcal{O}(\log T)$ for stochastic MABs, and $\mathcal{O}(\sqrt{T})$ for RL. We complement our theoretical findings with experimental results.

Submodular + Concave

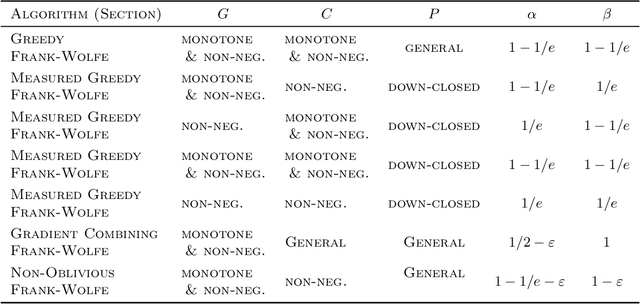
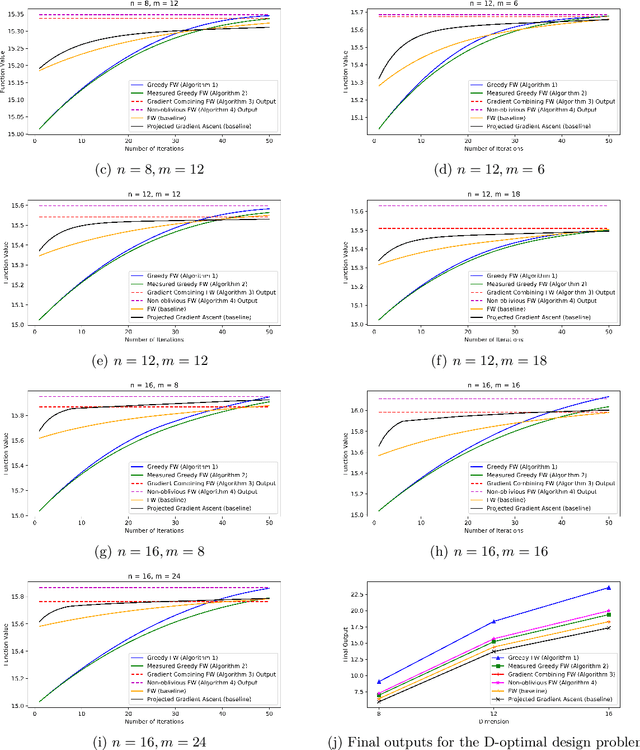
It has been well established that first order optimization methods can converge to the maximal objective value of concave functions and provide constant factor approximation guarantees for (non-convex/non-concave) continuous submodular functions. In this work, we initiate the study of the maximization of functions of the form $F(x) = G(x) +C(x)$ over a solvable convex body $P$, where $G$ is a smooth DR-submodular function and $C$ is a smooth concave function. This class of functions is a strict extension of both concave and continuous DR-submodular functions for which no theoretical guarantee is known. We provide a suite of Frank-Wolfe style algorithms, which, depending on the nature of the objective function (i.e., if $G$ and $C$ are monotone or not, and non-negative or not) and on the nature of the set $P$ (i.e., whether it is downward closed or not), provide $1-1/e$, $1/e$, or $1/2$ approximation guarantees. We then use our algorithms to get a framework to smoothly interpolate between choosing a diverse set of elements from a given ground set (corresponding to the mode of a determinantal point process) and choosing a clustered set of elements (corresponding to the maxima of a suitable concave function). Additionally, we apply our algorithms to various functions in the above class (DR-submodular + concave) in both constrained and unconstrained settings, and show that our algorithms consistently outperform natural baselines.

On Adaptivity in Information-constrained Online Learning

We study how to adapt to smoothly-varying (`easy') environments in well-known online learning problems where acquiring information is expensive. For the problem of label efficient prediction, which is a budgeted version of prediction with expert advice, we present an online algorithm whose regret depends optimally on the number of labels allowed and $Q^*$ (the quadratic variation of the losses of the best action in hindsight), along with a parameter-free counterpart whose regret depends optimally on $Q$ (the quadratic variation of the losses of all the actions). These quantities can be significantly smaller than $T$ (the total time horizon), yielding an improvement over existing, variation-independent results for the problem. We then extend our analysis to handle label efficient prediction with bandit feedback, i.e., label efficient bandits. Our work builds upon the framework of optimistic online mirror descent, and leverages second order corrections along with a carefully designed hybrid regularizer that encodes the constrained information structure of the problem. We then consider revealing action-partial monitoring games -- a version of label efficient prediction with additive information costs, which in general are known to lie in the \textit{hard} class of games having minimax regret of order $T^{\frac{2}{3}}$. We provide a strategy with an $\mathcal{O}((Q^*T)^{\frac{1}{3}})$ bound for revealing action games, along with an one with a $\mathcal{O}((QT)^{\frac{1}{3}})$ bound for the full class of hard partial monitoring games, both being strict improvements over current bounds.