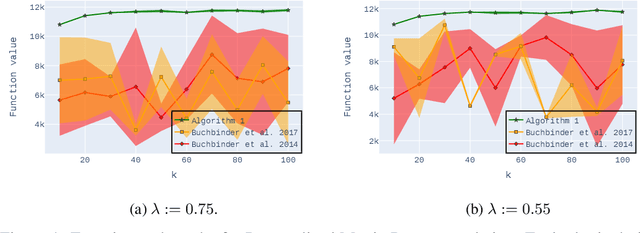
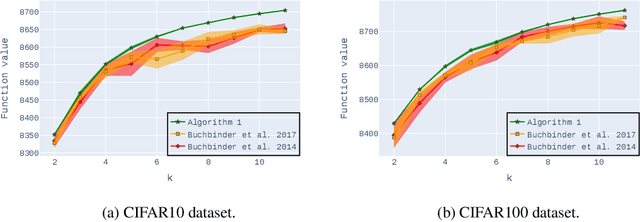
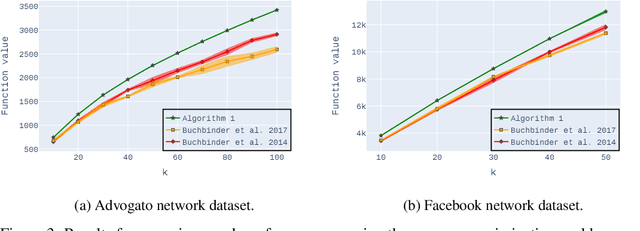
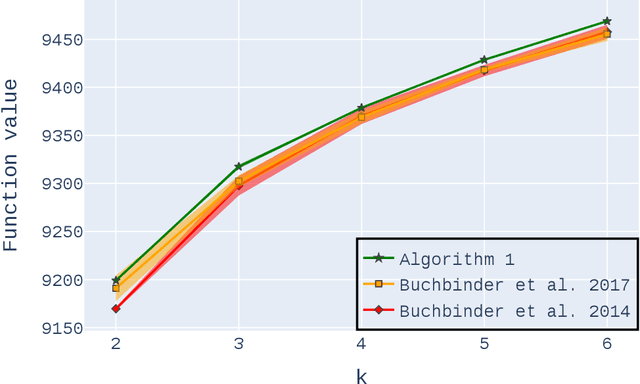
Practical $0.385$-Approximation for Submodular Maximization Subject to a Cardinality Constraint

Non-monotone constrained submodular maximization plays a crucial role in various machine learning applications. However, existing algorithms often struggle with a trade-off between approximation guarantees and practical efficiency. The current state-of-the-art is a recent $0.401$-approximation algorithm, but its computational complexity makes it highly impractical. The best practical algorithms for the problem only guarantee $1/e$-approximation. In this work, we present a novel algorithm for submodular maximization subject to a cardinality constraint that combines a guarantee of $0.385$-approximation with a low and practical query complexity of $O(n+k^2)$. Furthermore, we evaluate the empirical performance of our algorithm in experiments based on various machine learning applications, including Movie Recommendation, Image Summarization, and more. These experiments demonstrate the efficacy of our approach.

Bridging the Gap Between General and Down-Closed Convex Sets in Submodular Maximization

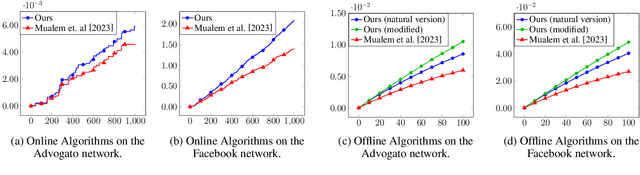
Optimization of DR-submodular functions has experienced a notable surge in significance in recent times, marking a pivotal development within the domain of non-convex optimization. Motivated by real-world scenarios, some recent works have delved into the maximization of non-monotone DR-submodular functions over general (not necessarily down-closed) convex set constraints. Up to this point, these works have all used the minimum $\ell_\infty$ norm of any feasible solution as a parameter. Unfortunately, a recent hardness result due to Mualem \& Feldman~\cite{mualem2023resolving} shows that this approach cannot yield a smooth interpolation between down-closed and non-down-closed constraints. In this work, we suggest novel offline and online algorithms that provably provide such an interpolation based on a natural decomposition of the convex body constraint into two distinct convex bodies: a down-closed convex body and a general convex body. We also empirically demonstrate the superiority of our proposed algorithms across three offline and two online applications.

ORBSLAM3-Enhanced Autonomous Toy Drones: Pioneering Indoor Exploration

Navigating toy drones through uncharted GPS-denied indoor spaces poses significant difficulties due to their reliance on GPS for location determination. In such circumstances, the necessity for achieving proper navigation is a primary concern. In response to this formidable challenge, we introduce a real-time autonomous indoor exploration system tailored for drones equipped with a monocular \emph{RGB} camera. Our system utilizes \emph{ORB-SLAM3}, a state-of-the-art vision feature-based SLAM, to handle both the localization of toy drones and the mapping of unmapped indoor terrains. Aside from the practicability of \emph{ORB-SLAM3}, the generated maps are represented as sparse point clouds, making them prone to the presence of outlier data. To address this challenge, we propose an outlier removal algorithm with provable guarantees. Furthermore, our system incorporates a novel exit detection algorithm, ensuring continuous exploration by the toy drone throughout the unfamiliar indoor environment. We also transform the sparse point to ensure proper path planning using existing path planners. To validate the efficacy and efficiency of our proposed system, we conducted offline and real-time experiments on the autonomous exploration of indoor spaces. The results from these endeavors demonstrate the effectiveness of our methods.

Submodular Minimax Optimization: Finding Effective Sets

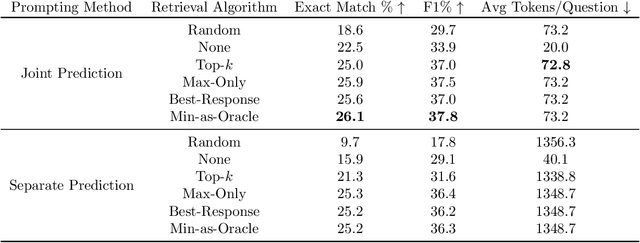
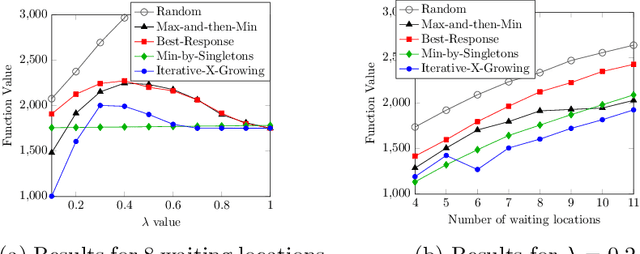
Despite the rich existing literature about minimax optimization in continuous settings, only very partial results of this kind have been obtained for combinatorial settings. In this paper, we fill this gap by providing a characterization of submodular minimax optimization, the problem of finding a set (for either the min or the max player) that is effective against every possible response. We show when and under what conditions we can find such sets. We also demonstrate how minimax submodular optimization provides robust solutions for downstream machine learning applications such as (i) efficient prompt engineering for question answering, (ii) prompt engineering for dialog state tracking, (iii) identifying robust waiting locations for ride-sharing, (iv) ride-share difficulty kernelization, and (v) finding adversarial images. Our experiments demonstrate that our proposed algorithms consistently outperform other baselines.

Resolving the Approximability of Offline and Online Non-monotone DR-Submodular Maximization over General Convex Sets

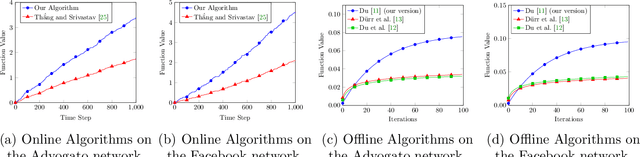
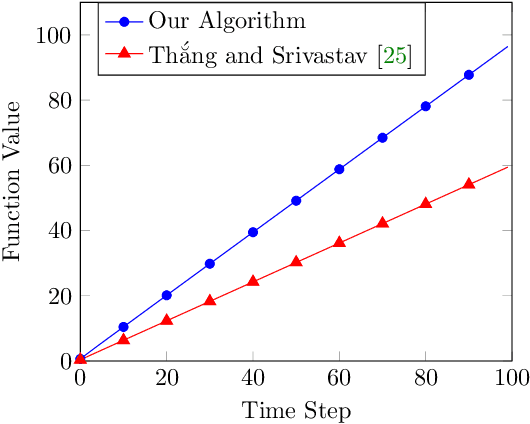
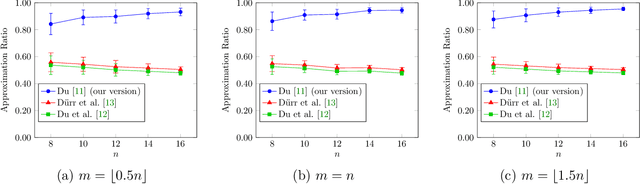
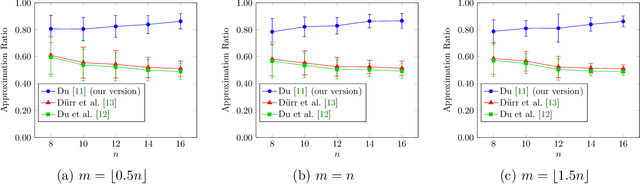
In recent years, maximization of DR-submodular continuous functions became an important research field, with many real-worlds applications in the domains of machine learning, communication systems, operation research and economics. Most of the works in this field study maximization subject to down-closed convex set constraints due to an inapproximability result by Vondr\'ak (2013). However, Durr et al. (2021) showed that one can bypass this inapproximability by proving approximation ratios that are functions of $m$, the minimum $\ell_{\infty}$-norm of any feasible vector. Given this observation, it is possible to get results for maximizing a DR-submodular function subject to general convex set constraints, which has led to multiple works on this problem. The most recent of which is a polynomial time $\tfrac{1}{4}(1 - m)$-approximation offline algorithm due to Du (2022). However, only a sub-exponential time $\tfrac{1}{3\sqrt{3}}(1 - m)$-approximation algorithm is known for the corresponding online problem. In this work, we present a polynomial time online algorithm matching the $\tfrac{1}{4}(1 - m)$-approximation of the state-of-the-art offline algorithm. We also present an inapproximability result showing that our online algorithm and Du's (2022) offline algorithm are both optimal in a strong sense. Finally, we study the empirical performance of our algorithm and the algorithm of Du (which was only theoretically studied previously), and show that they consistently outperform previously suggested algorithms on revenue maximization, location summarization and quadratic programming applications.

Pruning Neural Networks via Coresets and Convex Geometry: Towards No Assumptions

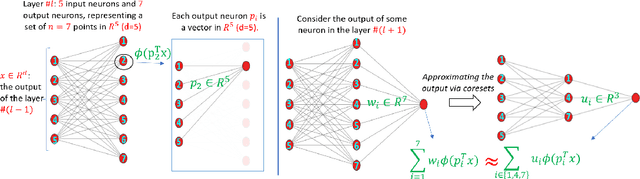
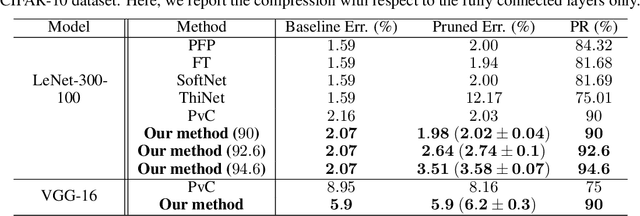
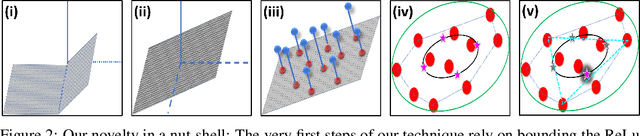
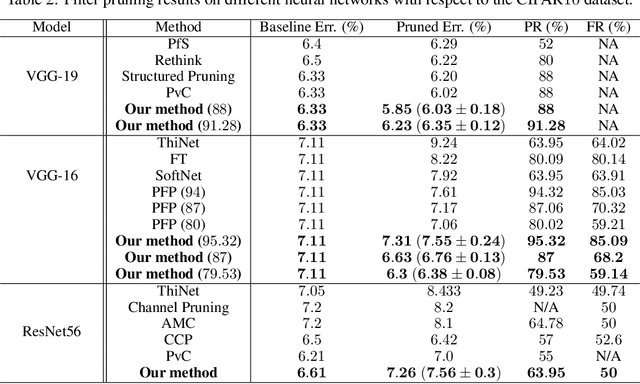
Pruning is one of the predominant approaches for compressing deep neural networks (DNNs). Lately, coresets (provable data summarizations) were leveraged for pruning DNNs, adding the advantage of theoretical guarantees on the trade-off between the compression rate and the approximation error. However, coresets in this domain were either data-dependent or generated under restrictive assumptions on both the model's weights and inputs. In real-world scenarios, such assumptions are rarely satisfied, limiting the applicability of coresets. To this end, we suggest a novel and robust framework for computing such coresets under mild assumptions on the model's weights and without any assumption on the training data. The idea is to compute the importance of each neuron in each layer with respect to the output of the following layer. This is achieved by a combination of L\"{o}wner ellipsoid and Caratheodory theorem. Our method is simultaneously data-independent, applicable to various networks and datasets (due to the simplified assumptions), and theoretically supported. Experimental results show that our method outperforms existing coreset based neural pruning approaches across a wide range of networks and datasets. For example, our method achieved a $62\%$ compression rate on ResNet50 on ImageNet with $1.09\%$ drop in accuracy.

Using Partial Monotonicity in Submodular Maximization

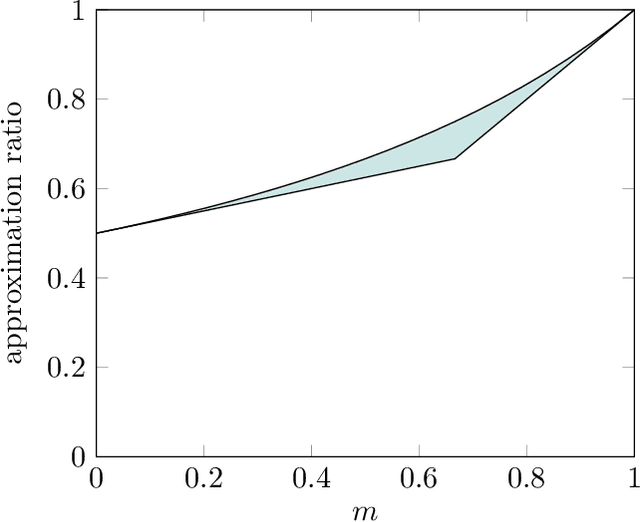
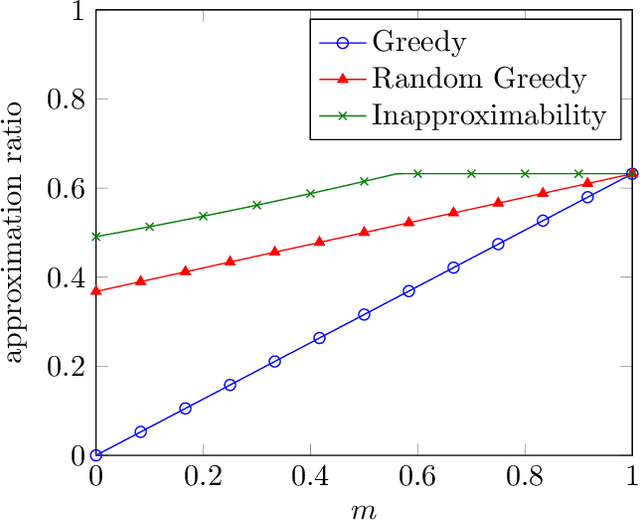
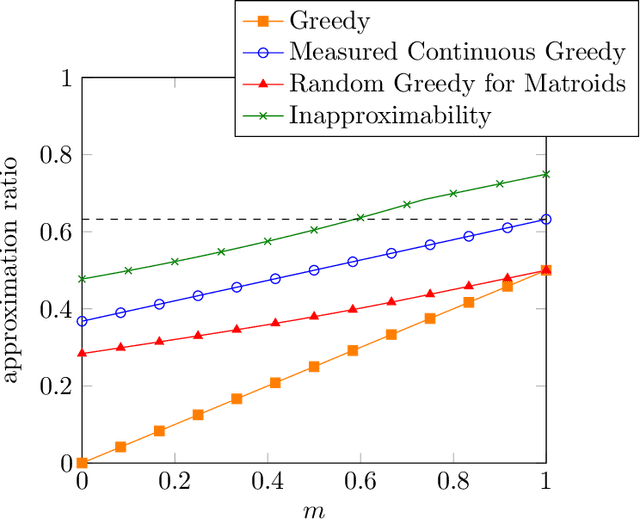
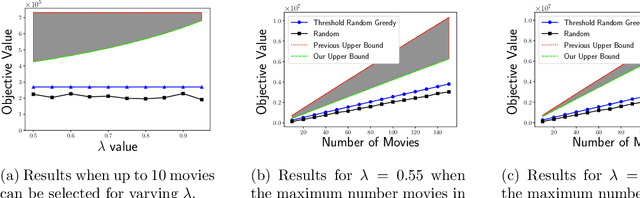
Over the last two decades, submodular function maximization has been the workhorse of many discrete optimization problems in machine learning applications. Traditionally, the study of submodular functions was based on binary function properties. However, such properties have an inherit weakness, namely, if an algorithm assumes functions that have a particular property, then it provides no guarantee for functions that violate this property, even when the violation is very slight. Therefore, recent works began to consider continuous versions of function properties. Probably the most significant among these (so far) are the submodularity ratio and the curvature, which were studied extensively together and separately. The monotonicity property of set functions plays a central role in submodular maximization. Nevertheless, and despite all the above works, no continuous version of this property has been suggested to date (as far as we know). This is unfortunate since submoduar functions that are almost monotone often arise in machine learning applications. In this work we fill this gap by defining the monotonicity ratio, which is a continues version of the monotonicity property. We then show that for many standard submodular maximization algorithms one can prove new approximation guarantees that depend on the monotonicity ratio; leading to improved approximation ratios for the common machine learning applications of movie recommendation, quadratic programming and image summarization.