Resolving the Approximability of Offline and Online Non-monotone DR-Submodular Maximization over General Convex Sets

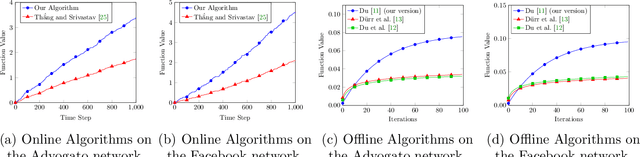
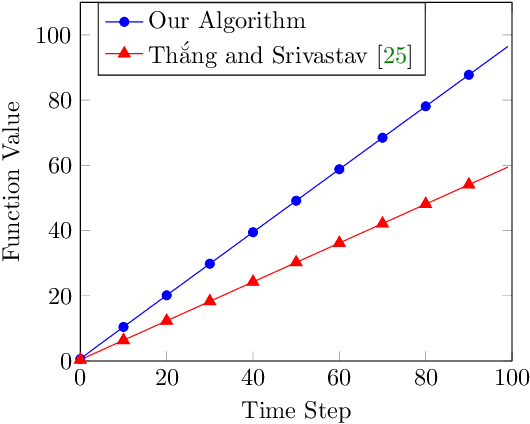
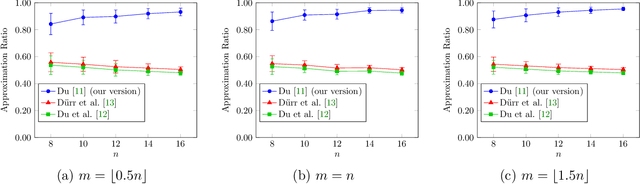
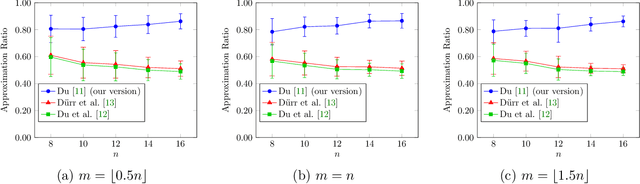
In recent years, maximization of DR-submodular continuous functions became an important research field, with many real-worlds applications in the domains of machine learning, communication systems, operation research and economics. Most of the works in this field study maximization subject to down-closed convex set constraints due to an inapproximability result by Vondr\'ak (2013). However, Durr et al. (2021) showed that one can bypass this inapproximability by proving approximation ratios that are functions of $m$, the minimum $\ell_{\infty}$-norm of any feasible vector. Given this observation, it is possible to get results for maximizing a DR-submodular function subject to general convex set constraints, which has led to multiple works on this problem. The most recent of which is a polynomial time $\tfrac{1}{4}(1 - m)$-approximation offline algorithm due to Du (2022). However, only a sub-exponential time $\tfrac{1}{3\sqrt{3}}(1 - m)$-approximation algorithm is known for the corresponding online problem. In this work, we present a polynomial time online algorithm matching the $\tfrac{1}{4}(1 - m)$-approximation of the state-of-the-art offline algorithm. We also present an inapproximability result showing that our online algorithm and Du's (2022) offline algorithm are both optimal in a strong sense. Finally, we study the empirical performance of our algorithm and the algorithm of Du (which was only theoretically studied previously), and show that they consistently outperform previously suggested algorithms on revenue maximization, location summarization and quadratic programming applications.