Thomas Kerdreux
Efficient Self-Supervised Learning for Earth Observation via Dynamic Dataset Curation
Apr 09, 2025
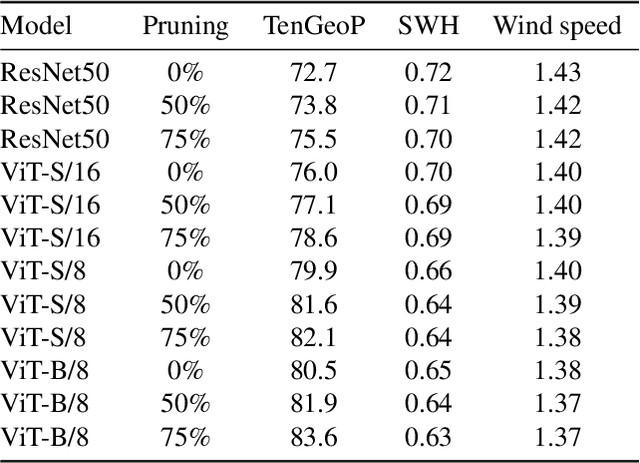
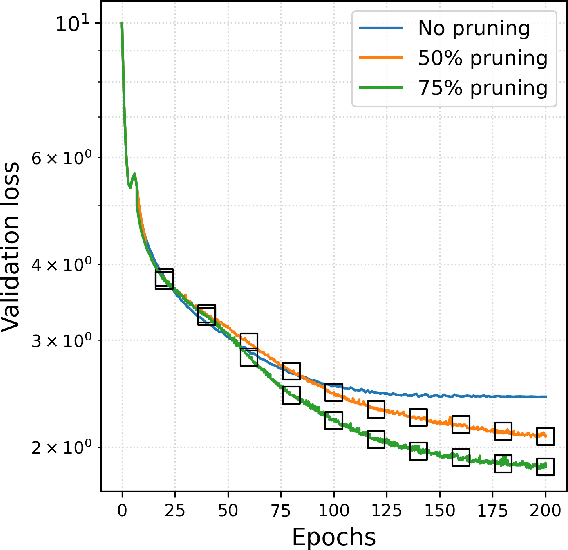
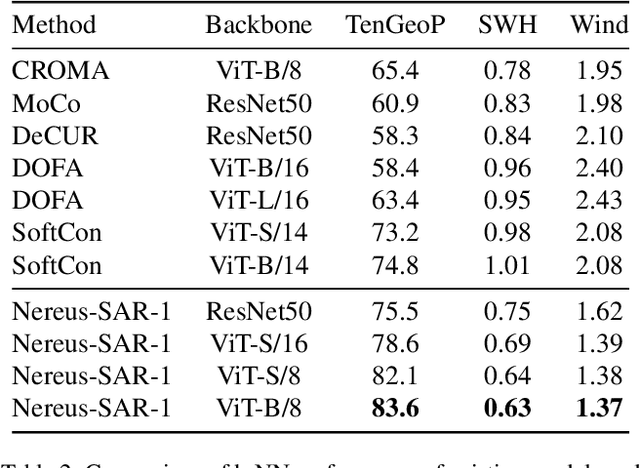
Abstract:Self-supervised learning (SSL) has enabled the development of vision foundation models for Earth Observation (EO), demonstrating strong transferability across diverse remote sensing tasks. While prior work has focused on network architectures and training strategies, the role of dataset curation, especially in balancing and diversifying pre-training datasets, remains underexplored. In EO, this challenge is amplified by the redundancy and heavy-tailed distributions common in satellite imagery, which can lead to biased representations and inefficient training. In this work, we propose a dynamic dataset pruning strategy designed to improve SSL pre-training by maximizing dataset diversity and balance. Our method iteratively refines the training set without requiring a pre-existing feature extractor, making it well-suited for domains where curated datasets are limited or unavailable. We demonstrate our approach on the Sentinel-1 Wave Mode (WV) Synthetic Aperture Radar (SAR) archive, a challenging dataset dominated by ocean observations. We train models from scratch on the entire Sentinel-1 WV archive spanning 10 years. Across three downstream tasks, our results show that dynamic pruning improves both computational efficiency and representation quality, leading to stronger transferability. We also release the weights of Nereus-SAR-1, the first model in the Nereus family, a series of foundation models for ocean observation and analysis using SAR imagery, at github.com/galeio-research/nereus-sar-models/.
Diffusion Models for Interferometric Satellite Aperture Radar
Aug 31, 2023Abstract:Probabilistic Diffusion Models (PDMs) have recently emerged as a very promising class of generative models, achieving high performance in natural image generation. However, their performance relative to non-natural images, like radar-based satellite data, remains largely unknown. Generating large amounts of synthetic (and especially labelled) satellite data is crucial to implement deep-learning approaches for the processing and analysis of (interferometric) satellite aperture radar data. Here, we leverage PDMs to generate several radar-based satellite image datasets. We show that PDMs succeed in generating images with complex and realistic structures, but that sampling time remains an issue. Indeed, accelerated sampling strategies, which work well on simple image datasets like MNIST, fail on our radar datasets. We provide a simple and versatile open-source https://github.com/thomaskerdreux/PDM_SAR_InSAR_generation to train, sample and evaluate PDMs using any dataset on a single GPU.
Autonomous Detection of Methane Emissions in Multispectral Satellite Data Using Deep Learning
Aug 21, 2023



Abstract:Methane is one of the most potent greenhouse gases, and its short atmospheric half-life makes it a prime target to rapidly curb global warming. However, current methane emission monitoring techniques primarily rely on approximate emission factors or self-reporting, which have been shown to often dramatically underestimate emissions. Although initially designed to monitor surface properties, satellite multispectral data has recently emerged as a powerful method to analyze atmospheric content. However, the spectral resolution of multispectral instruments is poor, and methane measurements are typically very noisy. Methane data products are also sensitive to absorption by the surface and other atmospheric gases (water vapor in particular) and therefore provide noisy maps of potential methane plumes, that typically require extensive human analysis. Here, we show that the image recognition capabilities of deep learning methods can be leveraged to automatize the detection of methane leaks in Sentinel-2 satellite multispectral data, with dramatically reduced false positive rates compared with state-of-the-art multispectral methane data products, and without the need for a priori knowledge of potential leak sites. Our proposed approach paves the way for the automated, high-definition and high-frequency monitoring of point-source methane emissions across the world.
Efficient Online-Bandit Strategies for Minimax Learning Problems
Jun 04, 2021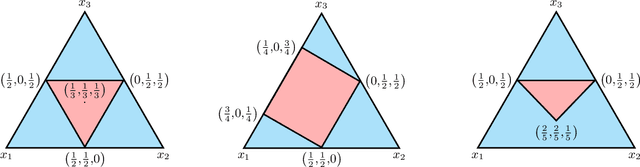
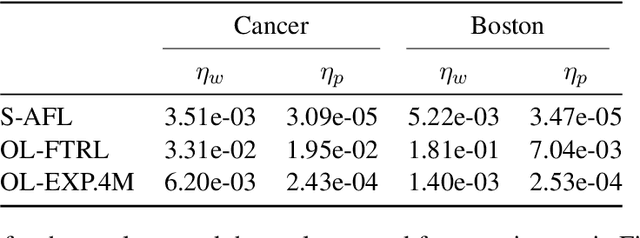
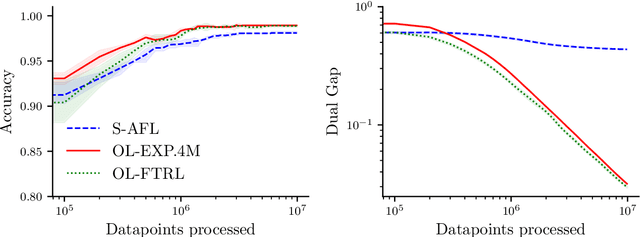

Abstract:Several learning problems involve solving min-max problems, e.g., empirical distributional robust learning or learning with non-standard aggregated losses. More specifically, these problems are convex-linear problems where the minimization is carried out over the model parameters $w\in\mathcal{W}$ and the maximization over the empirical distribution $p\in\mathcal{K}$ of the training set indexes, where $\mathcal{K}$ is the simplex or a subset of it. To design efficient methods, we let an online learning algorithm play against a (combinatorial) bandit algorithm. We argue that the efficiency of such approaches critically depends on the structure of $\mathcal{K}$ and propose two properties of $\mathcal{K}$ that facilitate designing efficient algorithms. We focus on a specific family of sets $\mathcal{S}_{n,k}$ encompassing various learning applications and provide high-probability convergence guarantees to the minimax values.
Linear Bandits on Uniformly Convex Sets
Mar 10, 2021Abstract:Linear bandit algorithms yield $\tilde{\mathcal{O}}(n\sqrt{T})$ pseudo-regret bounds on compact convex action sets $\mathcal{K}\subset\mathbb{R}^n$ and two types of structural assumptions lead to better pseudo-regret bounds. When $\mathcal{K}$ is the simplex or an $\ell_p$ ball with $p\in]1,2]$, there exist bandits algorithms with $\tilde{\mathcal{O}}(\sqrt{nT})$ pseudo-regret bounds. Here, we derive bandit algorithms for some strongly convex sets beyond $\ell_p$ balls that enjoy pseudo-regret bounds of $\tilde{\mathcal{O}}(\sqrt{nT})$, which answers an open question from [BCB12, \S 5.5.]. Interestingly, when the action set is uniformly convex but not necessarily strongly convex, we obtain pseudo-regret bounds with a dimension dependency smaller than $\mathcal{O}(\sqrt{n})$. However, this comes at the expense of asymptotic rates in $T$ varying between $\tilde{\mathcal{O}}(\sqrt{T})$ and $\tilde{\mathcal{O}}(T)$.
Local and Global Uniform Convexity Conditions
Feb 18, 2021Abstract:We review various characterizations of uniform convexity and smoothness on norm balls in finite-dimensional spaces and connect results stemming from the geometry of Banach spaces with \textit{scaling inequalities} used in analysing the convergence of optimization methods. In particular, we establish local versions of these conditions to provide sharper insights on a recent body of complexity results in learning theory, online learning, or offline optimization, which rely on the strong convexity of the feasible set. While they have a significant impact on complexity, these strong convexity or uniform convexity properties of feasible sets are not exploited as thoroughly as their functional counterparts, and this work is an effort to correct this imbalance. We conclude with some practical examples in optimization and machine learning where leveraging these conditions and localized assumptions lead to new complexity results.
Generating Structured Adversarial Attacks Using Frank-Wolfe Method
Feb 15, 2021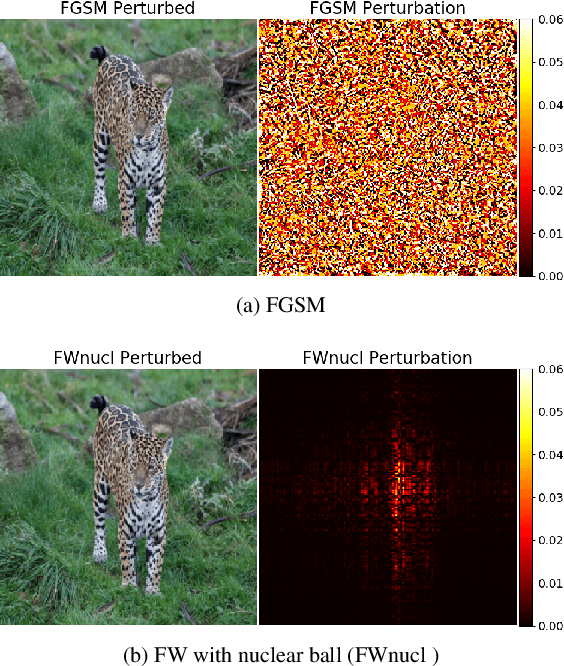

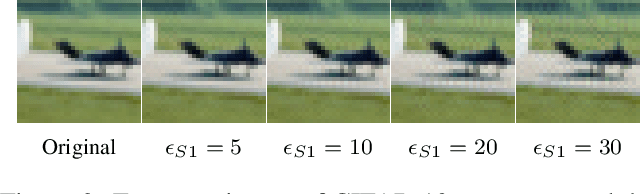

Abstract:White box adversarial perturbations are generated via iterative optimization algorithms most often by minimizing an adversarial loss on a $\ell_p$ neighborhood of the original image, the so-called distortion set. Constraining the adversarial search with different norms results in disparately structured adversarial examples. Here we explore several distortion sets with structure-enhancing algorithms. These new structures for adversarial examples might provide challenges for provable and empirical robust mechanisms. Because adversarial robustness is still an empirical field, defense mechanisms should also reasonably be evaluated against differently structured attacks. Besides, these structured adversarial perturbations may allow for larger distortions size than their $\ell_p$ counter-part while remaining imperceptible or perceptible as natural distortions of the image. We will demonstrate in this work that the proposed structured adversarial examples can significantly bring down the classification accuracy of adversarialy trained classifiers while showing low $\ell_2$ distortion rate. For instance, on ImagNet dataset the structured attacks drop the accuracy of adversarial model to near zero with only 50\% of $\ell_2$ distortion generated using white-box attacks like PGD. As a byproduct, our finding on structured adversarial examples can be used for adversarial regularization of models to make models more robust or improve their generalization performance on datasets which are structurally different.
Diptychs of human and machine perceptions
Oct 12, 2020

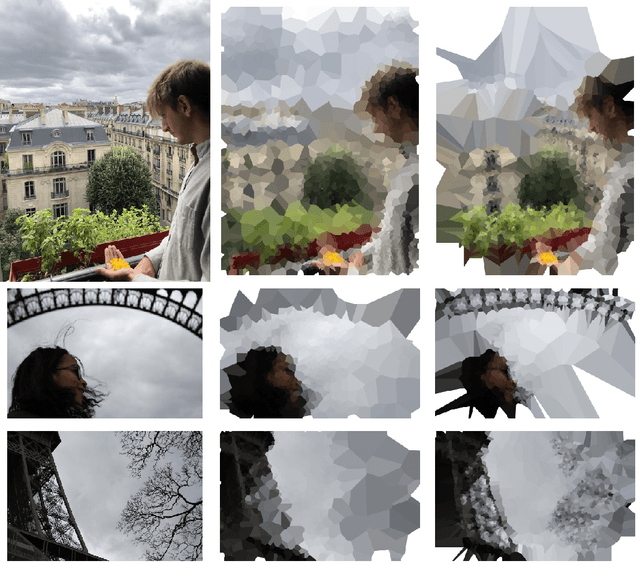

Abstract:We propose visual creations that put differences in algorithms and humans \emph{perceptions} into perspective. We exploit saliency maps of neural networks and visual focus of humans to create diptychs that are reinterpretations of an original image according to both machine and human attentions. Using those diptychs as a qualitative evaluation of perception, we discuss some crucial issues of current \textit{task-oriented} artificial intelligence.
Trace-Norm Adversarial Examples
Jul 02, 2020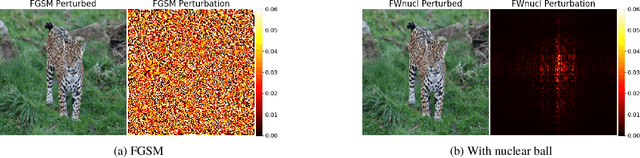
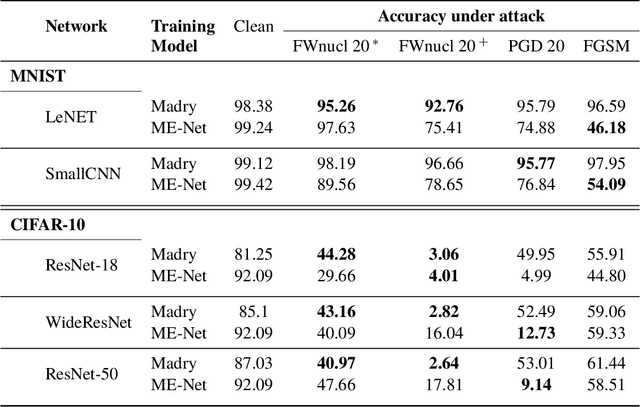

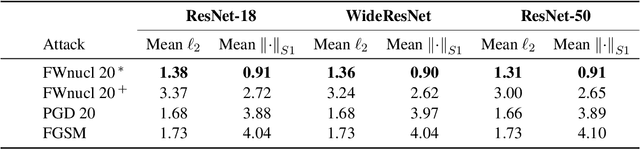
Abstract:White box adversarial perturbations are sought via iterative optimization algorithms most often minimizing an adversarial loss on a $l_p$ neighborhood of the original image, the so-called distortion set. Constraining the adversarial search with different norms results in disparately structured adversarial examples. Here we explore several distortion sets with structure-enhancing algorithms. These new structures for adversarial examples, yet pervasive in optimization, are for instance a challenge for adversarial theoretical certification which again provides only $l_p$ certificates. Because adversarial robustness is still an empirical field, defense mechanisms should also reasonably be evaluated against differently structured attacks. Besides, these structured adversarial perturbations may allow for larger distortions size than their $l_p$ counter-part while remaining imperceptible or perceptible as natural slight distortions of the image. Finally, they allow some control on the generation of the adversarial perturbation, like (localized) bluriness.
Interactive Neural Style Transfer with Artists
Mar 14, 2020



Abstract:We present interactive painting processes in which a painter and various neural style transfer algorithms interact on a real canvas. Understanding what these algorithms' outputs achieve is then paramount to describe the creative agency in our interactive experiments. We gather a set of paired painting-pictures images and present a new evaluation methodology based on the predictivity of neural style transfer algorithms. We point some algorithms' instabilities and show that they can be used to enlarge the diversity and pleasing oddity of the images synthesized by the numerous existing neural style transfer algorithms. This diversity of images was perceived as a source of inspiration for human painters, portraying the machine as a computational catalyst.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge