Relaxing Anchor-Frame Dominance for Mitigating Hallucinations in Video Large Language Models

Recent Video Large Language Models (Video-LLMs) have demonstrated strong capability in video understanding, yet they still suffer from hallucinations. Existing mitigation methods typically rely on training, input modification, auxiliary guidance, or additional decoding procedures, while largely overlooking a more fundamental challenge. During generation, Video-LLMs tend to over-rely on a limited portion of temporal evidence, leading to temporally imbalanced evidence aggregation across the video. To address this issue, we investigate a decoder-side phenomenon in which the model exhibits a temporally imbalanced concentration pattern. We term the frame with the highest aggregated frame-level attention mass the anchor frame. We find that this bias is largely independent of the input video and instead appears to reflect a persistent, model-specific structural or positional bias, whose over-dominance is closely associated with hallucination-prone generation. Motivated by this insight, we propose Decoder-side Temporal Rebalancing (DTR), a training-free, layer-selective inference method that rebalances temporal evidence allocation in middle-to-late decoder layers without altering visual encoding or requiring auxiliary models. DTR adaptively calibrates decoder-side visual attention to alleviate temporally imbalanced concentration and encourage under-attended frames to contribute more effectively to response generation. In this way, DTR guides the decoder to ground its outputs in temporally broader and more balanced video evidence. Extensive experiments on hallucination and video understanding benchmarks show that DTR consistently improves hallucination robustness across diverse Video-LLM families, while preserving competitive video understanding performance and high inference efficiency.

HTNav: A Hybrid Navigation Framework with Tiered Structure for Urban Aerial Vision-and-Language Navigation

Inspired by the general Vision-and-Language Navigation (VLN) task, aerial VLN has attracted widespread attention, owing to its significant practical value in applications such as logistics delivery and urban inspection. However, existing methods face several challenges in complex urban environments, including insufficient generalization to unseen scenes, suboptimal performance in long-range path planning, and inadequate understanding of spatial continuity. To address these challenges, we propose HTNav, a new collaborative navigation framework that integrates Imitation Learning (IL) and Reinforcement Learning (RL) within a hybrid IL-RL framework. This framework adopts a staged training mechanism to ensure the stability of the basic navigation strategy while enhancing its environmental exploration capability. By integrating a tiered decision-making mechanism, it achieves collaborative interaction between macro-level path planning and fine-grained action control. Furthermore, a map representation learning module is introduced to deepen its understanding of spatial continuity in open domains. On the CityNav benchmark, our method achieves state-of-the-art performance across all scene levels and task difficulties. Experimental results demonstrate that this framework significantly improves navigation precision and robustness in complex urban environments.

FutureX-Pro: Extending Future Prediction to High-Value Vertical Domains

Building upon FutureX, which established a live benchmark for general-purpose future prediction, this report introduces FutureX-Pro, including FutureX-Finance, FutureX-Retail, FutureX-PublicHealth, FutureX-NaturalDisaster, and FutureX-Search. These together form a specialized framework extending agentic future prediction to high-value vertical domains. While generalist agents demonstrate proficiency in open-domain search, their reliability in capital-intensive and safety-critical sectors remains under-explored. FutureX-Pro targets four economically and socially pivotal verticals: Finance, Retail, Public Health, and Natural Disaster. We benchmark agentic Large Language Models (LLMs) on entry-level yet foundational prediction tasks -- ranging from forecasting market indicators and supply chain demands to tracking epidemic trends and natural disasters. By adapting the contamination-free, live-evaluation pipeline of FutureX, we assess whether current State-of-the-Art (SOTA) agentic LLMs possess the domain grounding necessary for industrial deployment. Our findings reveal the performance gap between generalist reasoning and the precision required for high-value vertical applications.

HiGR: Efficient Generative Slate Recommendation via Hierarchical Planning and Multi-Objective Preference Alignment

Slate recommendation, where users are presented with a ranked list of items simultaneously, is widely adopted in online platforms. Recent advances in generative models have shown promise in slate recommendation by modeling sequences of discrete semantic IDs autoregressively. However, existing autoregressive approaches suffer from semantically entangled item tokenization and inefficient sequential decoding that lacks holistic slate planning. To address these limitations, we propose HiGR, an efficient generative slate recommendation framework that integrates hierarchical planning with listwise preference alignment. First, we propose an auto-encoder utilizing residual quantization and contrastive constraints to tokenize items into semantically structured IDs for controllable generation. Second, HiGR decouples generation into a list-level planning stage for global slate intent, followed by an item-level decoding stage for specific item selection. Third, we introduce a listwise preference alignment objective to directly optimize slate quality using implicit user feedback. Experiments on our large-scale commercial media platform demonstrate that HiGR delivers consistent improvements in both offline evaluations and online deployment. Specifically, it outperforms state-of-the-art methods by over 10% in offline recommendation quality with a 5x inference speedup, while further achieving a 1.22% and 1.73% increase in Average Watch Time and Average Video Views in online A/B tests.

Clipped Gradient Methods for Nonsmooth Convex Optimization under Heavy-Tailed Noise: A Refined Analysis

Optimization under heavy-tailed noise has become popular recently, since it better fits many modern machine learning tasks, as captured by empirical observations. Concretely, instead of a finite second moment on gradient noise, a bounded ${\frak p}$-th moment where ${\frak p}\in(1,2]$ has been recognized to be more realistic (say being upper bounded by $σ_{\frak l}^{\frak p}$ for some $σ_{\frak l}\ge0$). A simple yet effective operation, gradient clipping, is known to handle this new challenge successfully. Specifically, Clipped Stochastic Gradient Descent (Clipped SGD) guarantees a high-probability rate ${\cal O}(σ_{\frak l}\ln(1/δ)T^{1/{\frak p}-1})$ (resp. ${\cal O}(σ_{\frak l}^2\ln^2(1/δ)T^{2/{\frak p}-2})$) for nonsmooth convex (resp. strongly convex) problems, where $δ\in(0,1]$ is the failure probability and $T\in\mathbb{N}$ is the time horizon. In this work, we provide a refined analysis for Clipped SGD and offer two faster rates, ${\cal O}(σ_{\frak l}d_{\rm eff}^{-1/2{\frak p}}\ln^{1-1/{\frak p}}(1/δ)T^{1/{\frak p}-1})$ and ${\cal O}(σ_{\frak l}^2d_{\rm eff}^{-1/{\frak p}}\ln^{2-2/{\frak p}}(1/δ)T^{2/{\frak p}-2})$, than the aforementioned best results, where $d_{\rm eff}\ge1$ is a quantity we call the $\textit{generalized effective dimension}$. Our analysis improves upon the existing approach on two sides: better utilization of Freedman's inequality and finer bounds for clipping error under heavy-tailed noise. In addition, we extend the refined analysis to convergence in expectation and obtain new rates that break the known lower bounds. Lastly, to complement the study, we establish new lower bounds for both high-probability and in-expectation convergence. Notably, the in-expectation lower bounds match our new upper bounds, indicating the optimality of our refined analysis for convergence in expectation.

Online Convex Optimization with Heavy Tails: Old Algorithms, New Regrets, and Applications

In Online Convex Optimization (OCO), when the stochastic gradient has a finite variance, many algorithms provably work and guarantee a sublinear regret. However, limited results are known if the gradient estimate has a heavy tail, i.e., the stochastic gradient only admits a finite $\mathsf{p}$-th central moment for some $\mathsf{p}\in\left(1,2\right]$. Motivated by it, this work examines different old algorithms for OCO (e.g., Online Gradient Descent) in the more challenging heavy-tailed setting. Under the standard bounded domain assumption, we establish new regrets for these classical methods without any algorithmic modification. Remarkably, these regret bounds are fully optimal in all parameters (can be achieved even without knowing $\mathsf{p}$), suggesting that OCO with heavy tails can be solved effectively without any extra operation (e.g., gradient clipping). Our new results have several applications. A particularly interesting one is the first provable convergence result for nonsmooth nonconvex optimization under heavy-tailed noise without gradient clipping. Furthermore, we explore broader settings (e.g., smooth OCO) and extend our ideas to optimistic algorithms to handle different cases simultaneously.

Improved Last-Iterate Convergence of Shuffling Gradient Methods for Nonsmooth Convex Optimization

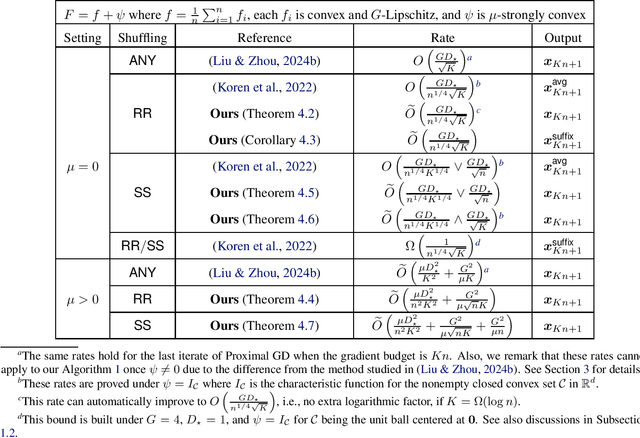
We study the convergence of the shuffling gradient method, a popular algorithm employed to minimize the finite-sum function with regularization, in which functions are passed to apply (Proximal) Gradient Descent (GD) one by one whose order is determined by a permutation on the indices of functions. In contrast to its easy implementation and effective performance in practice, the theoretical understanding remains limited. A recent advance by (Liu & Zhou, 2024b) establishes the first last-iterate convergence results under various settings, especially proving the optimal rates for smooth (strongly) convex optimization. However, their bounds for nonsmooth (strongly) convex functions are only as fast as Proximal GD. In this work, we provide the first improved last-iterate analysis for the nonsmooth case demonstrating that the widely used Random Reshuffle ($\textsf{RR}$) and Single Shuffle ($\textsf{SS}$) strategies are both provably faster than Proximal GD, reflecting the benefit of randomness. As an important implication, we give the first (nearly) optimal convergence result for the suffix average under the $\textsf{RR}$ sampling scheme in the general convex case, matching the lower bound shown by (Koren et al., 2022).

Nonconvex Stochastic Optimization under Heavy-Tailed Noises: Optimal Convergence without Gradient Clipping

Recently, the study of heavy-tailed noises in first-order nonconvex stochastic optimization has gotten a lot of attention since it was recognized as a more realistic condition as suggested by many empirical observations. Specifically, the stochastic noise (the difference between the stochastic and true gradient) is considered only to have a finite $\mathfrak{p}$-th moment where $\mathfrak{p}\in\left(1,2\right]$ instead of assuming it always satisfies the classical finite variance assumption. To deal with this more challenging setting, people have proposed different algorithms and proved them to converge at an optimal $\mathcal{O}(T^{\frac{1-\mathfrak{p}}{3\mathfrak{p}-2}})$ rate for smooth objectives after $T$ iterations. Notably, all these new-designed algorithms are based on the same technique - gradient clipping. Naturally, one may want to know whether the clipping method is a necessary ingredient and the only way to guarantee convergence under heavy-tailed noises. In this work, by revisiting the existing Batched Normalized Stochastic Gradient Descent with Momentum (Batched NSGDM) algorithm, we provide the first convergence result under heavy-tailed noises but without gradient clipping. Concretely, we prove that Batched NSGDM can achieve the optimal $\mathcal{O}(T^{\frac{1-\mathfrak{p}}{3\mathfrak{p}-2}})$ rate even under the relaxed smooth condition. More interestingly, we also establish the first $\mathcal{O}(T^{\frac{1-\mathfrak{p}}{2\mathfrak{p}}})$ convergence rate in the case where the tail index $\mathfrak{p}$ is unknown in advance, which is arguably the common scenario in practice.

On the Last-Iterate Convergence of Shuffling Gradient Methods

Shuffling gradient methods, which are also known as stochastic gradient descent (SGD) without replacement, are widely implemented in practice, particularly including three popular algorithms: Random Reshuffle (RR), Shuffle Once (SO), and Incremental Gradient (IG). Compared to the empirical success, the theoretical guarantee of shuffling gradient methods was not well-understanding for a long time. Until recently, the convergence rates had just been established for the average iterate for convex functions and the last iterate for strongly convex problems (using squared distance as the metric). However, when using the function value gap as the convergence criterion, existing theories cannot interpret the good performance of the last iterate in different settings (e.g., constrained optimization). To bridge this gap between practice and theory, we prove last-iterate convergence rates for shuffling gradient methods with respect to the objective value even without strong convexity. Our new results either (nearly) match the existing last-iterate lower bounds or are as fast as the previous best upper bounds for the average iterate.

Revisiting the Last-Iterate Convergence of Stochastic Gradient Methods

In the past several years, the convergence of the last iterate of the Stochastic Gradient Descent (SGD) algorithm has triggered people's interest due to its good performance in practice but lack of theoretical understanding. For Lipschitz and convex functions, different works have established the optimal $O(\log(1/\delta)\log T/\sqrt{T})$ or $O(\sqrt{\log(1/\delta)/T})$ high-probability convergence rates for the final iterate, where $T$ is the time horizon and $\delta$ is the failure probability. However, to prove these bounds, all the existing works are limited to compact domains or require almost surely bounded noises. It is natural to ask whether the last iterate of SGD can still guarantee the optimal convergence rate but without these two restrictive assumptions. Besides this important question, there are still lots of theoretical problems lacking an answer. For example, compared with the last iterate convergence of SGD for non-smooth problems, only few results for smooth optimization have yet been developed. Additionally, the existing results are all limited to a non-composite objective and the standard Euclidean norm. It still remains unclear whether the last-iterate convergence can be provably extended to wider composite optimization and non-Euclidean norms. In this work, to address the issues mentioned above, we revisit the last-iterate convergence of stochastic gradient methods and provide the first unified way to prove the convergence rates both in expectation and in high probability to accommodate general domains, composite objectives, non-Euclidean norms, Lipschitz conditions, smoothness and (strong) convexity simultaneously. Additionally, we extend our analysis to obtain the last-iterate convergence under heavy-tailed noises.