Zhengyuan Zhou
Optimal Bayesian Stopping for Efficient Inference of Consistent LLM Answers
Feb 05, 2026Abstract:A simple strategy for improving LLM accuracy, especially in math and reasoning problems, is to sample multiple responses and submit the answer most consistently reached. In this paper we leverage Bayesian prior information to save on sampling costs, stopping once sufficient consistency is reached. Although the exact posterior is computationally intractable, we further introduce an efficient "L-aggregated" stopping policy that tracks only the L-1 most frequent answer counts. Theoretically, we prove that L=3 is all you need: this coarse approximation is sufficient to achieve asymptotic optimality, and strictly dominates prior-free baselines, while having a fast posterior computation. Empirically, this identifies the most consistent (i.e., mode) LLM answer using fewer samples, and can achieve similar answer accuracy while cutting the number of LLM calls (i.e., saving on LLM inference costs) by up to 50%.
Surface-based Molecular Design with Multi-modal Flow Matching
Jan 08, 2026Abstract:Therapeutic peptides show promise in targeting previously undruggable binding sites, with recent advancements in deep generative models enabling full-atom peptide co-design for specific protein receptors. However, the critical role of molecular surfaces in protein-protein interactions (PPIs) has been underexplored. To bridge this gap, we propose an omni-design peptides generation paradigm, called SurfFlow, a novel surface-based generative algorithm that enables comprehensive co-design of sequence, structure, and surface for peptides. SurfFlow employs a multi-modality conditional flow matching (CFM) architecture to learn distributions of surface geometries and biochemical properties, enhancing peptide binding accuracy. Evaluated on the comprehensive PepMerge benchmark, SurfFlow consistently outperforms full-atom baselines across all metrics. These results highlight the advantages of considering molecular surfaces in de novo peptide discovery and demonstrate the potential of integrating multiple protein modalities for more effective therapeutic peptide discovery.
DR-SAC: Distributionally Robust Soft Actor-Critic for Reinforcement Learning under Uncertainty
Jun 14, 2025Abstract:Deep reinforcement learning (RL) has achieved significant success, yet its application in real-world scenarios is often hindered by a lack of robustness to environmental uncertainties. To solve this challenge, some robust RL algorithms have been proposed, but most are limited to tabular settings. In this work, we propose Distributionally Robust Soft Actor-Critic (DR-SAC), a novel algorithm designed to enhance the robustness of the state-of-the-art Soft Actor-Critic (SAC) algorithm. DR-SAC aims to maximize the expected value with entropy against the worst possible transition model lying in an uncertainty set. A distributionally robust version of the soft policy iteration is derived with a convergence guarantee. For settings where nominal distributions are unknown, such as offline RL, a generative modeling approach is proposed to estimate the required nominal distributions from data. Furthermore, experimental results on a range of continuous control benchmark tasks demonstrate our algorithm achieves up to $9.8$ times the average reward of the SAC baseline under common perturbations. Additionally, compared with existing robust reinforcement learning algorithms, DR-SAC significantly improves computing efficiency and applicability to large-scale problems.
Improved Last-Iterate Convergence of Shuffling Gradient Methods for Nonsmooth Convex Optimization
May 29, 2025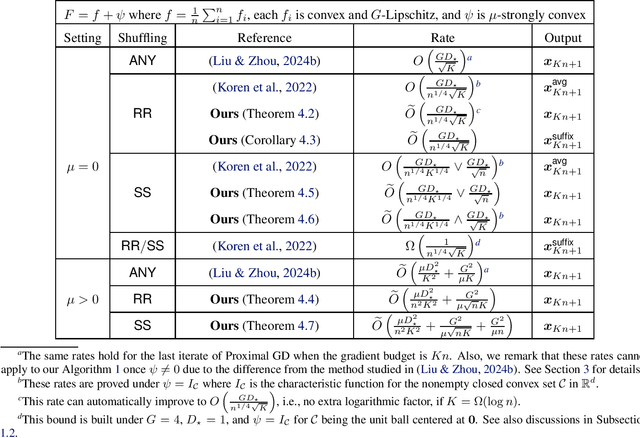
Abstract:We study the convergence of the shuffling gradient method, a popular algorithm employed to minimize the finite-sum function with regularization, in which functions are passed to apply (Proximal) Gradient Descent (GD) one by one whose order is determined by a permutation on the indices of functions. In contrast to its easy implementation and effective performance in practice, the theoretical understanding remains limited. A recent advance by (Liu & Zhou, 2024b) establishes the first last-iterate convergence results under various settings, especially proving the optimal rates for smooth (strongly) convex optimization. However, their bounds for nonsmooth (strongly) convex functions are only as fast as Proximal GD. In this work, we provide the first improved last-iterate analysis for the nonsmooth case demonstrating that the widely used Random Reshuffle ($\textsf{RR}$) and Single Shuffle ($\textsf{SS}$) strategies are both provably faster than Proximal GD, reflecting the benefit of randomness. As an important implication, we give the first (nearly) optimal convergence result for the suffix average under the $\textsf{RR}$ sampling scheme in the general convex case, matching the lower bound shown by (Koren et al., 2022).
Joint Value Estimation and Bidding in Repeated First-Price Auctions
Feb 24, 2025Abstract:We study regret minimization in repeated first-price auctions (FPAs), where a bidder observes only the realized outcome after each auction -- win or loss. This setup reflects practical scenarios in online display advertising where the actual value of an impression depends on the difference between two potential outcomes, such as clicks or conversion rates, when the auction is won versus lost. We analyze three outcome models: (1) adversarial outcomes without features, (2) linear potential outcomes with features, and (3) linear treatment effects in features. For each setting, we propose algorithms that jointly estimate private values and optimize bidding strategies, achieving near-optimal regret bounds. Notably, our framework enjoys a unique feature that the treatments are also actively chosen, and hence eliminates the need for the overlap condition commonly required in causal inference.
Learning an Optimal Assortment Policy under Observational Data
Feb 10, 2025Abstract:We study the fundamental problem of offline assortment optimization under the Multinomial Logit (MNL) model, where sellers must determine the optimal subset of the products to offer based solely on historical customer choice data. While most existing approaches to learning-based assortment optimization focus on the online learning of the optimal assortment through repeated interactions with customers, such exploration can be costly or even impractical in many real-world settings. In this paper, we consider the offline learning paradigm and investigate the minimal data requirements for efficient offline assortment optimization. To this end, we introduce Pessimistic Rank-Breaking (PRB), an algorithm that combines rank-breaking with pessimistic estimation. We prove that PRB is nearly minimax optimal by establishing the tight suboptimality upper bound and a nearly matching lower bound. This further shows that "optimal item coverage" - where each item in the optimal assortment appears sufficiently often in the historical data - is both sufficient and necessary for efficient offline learning. This significantly relaxes the previous requirement of observing the complete optimal assortment in the data. Our results provide fundamental insights into the data requirements for offline assortment optimization under the MNL model.
Nonconvex Stochastic Optimization under Heavy-Tailed Noises: Optimal Convergence without Gradient Clipping
Dec 27, 2024Abstract:Recently, the study of heavy-tailed noises in first-order nonconvex stochastic optimization has gotten a lot of attention since it was recognized as a more realistic condition as suggested by many empirical observations. Specifically, the stochastic noise (the difference between the stochastic and true gradient) is considered only to have a finite $\mathfrak{p}$-th moment where $\mathfrak{p}\in\left(1,2\right]$ instead of assuming it always satisfies the classical finite variance assumption. To deal with this more challenging setting, people have proposed different algorithms and proved them to converge at an optimal $\mathcal{O}(T^{\frac{1-\mathfrak{p}}{3\mathfrak{p}-2}})$ rate for smooth objectives after $T$ iterations. Notably, all these new-designed algorithms are based on the same technique - gradient clipping. Naturally, one may want to know whether the clipping method is a necessary ingredient and the only way to guarantee convergence under heavy-tailed noises. In this work, by revisiting the existing Batched Normalized Stochastic Gradient Descent with Momentum (Batched NSGDM) algorithm, we provide the first convergence result under heavy-tailed noises but without gradient clipping. Concretely, we prove that Batched NSGDM can achieve the optimal $\mathcal{O}(T^{\frac{1-\mathfrak{p}}{3\mathfrak{p}-2}})$ rate even under the relaxed smooth condition. More interestingly, we also establish the first $\mathcal{O}(T^{\frac{1-\mathfrak{p}}{2\mathfrak{p}}})$ convergence rate in the case where the tail index $\mathfrak{p}$ is unknown in advance, which is arguably the common scenario in practice.
Distributionally Robust Policy Learning under Concept Drifts
Dec 18, 2024Abstract:Distributionally robust policy learning aims to find a policy that performs well under the worst-case distributional shift, and yet most existing methods for robust policy learning consider the worst-case joint distribution of the covariate and the outcome. The joint-modeling strategy can be unnecessarily conservative when we have more information on the source of distributional shifts. This paper studiesa more nuanced problem -- robust policy learning under the concept drift, when only the conditional relationship between the outcome and the covariate changes. To this end, we first provide a doubly-robust estimator for evaluating the worst-case average reward of a given policy under a set of perturbed conditional distributions. We show that the policy value estimator enjoys asymptotic normality even if the nuisance parameters are estimated with a slower-than-root-$n$ rate. We then propose a learning algorithm that outputs the policy maximizing the estimated policy value within a given policy class $\Pi$, and show that the sub-optimality gap of the proposed algorithm is of the order $\kappa(\Pi)n^{-1/2}$, with $\kappa(\Pi)$ is the entropy integral of $\Pi$ under the Hamming distance and $n$ is the sample size. A matching lower bound is provided to show the optimality of the rate. The proposed methods are implemented and evaluated in numerical studies, demonstrating substantial improvement compared with existing benchmarks.
Statistical Learning of Distributionally Robust Stochastic Control in Continuous State Spaces
Jun 17, 2024
Abstract:We explore the control of stochastic systems with potentially continuous state and action spaces, characterized by the state dynamics $X_{t+1} = f(X_t, A_t, W_t)$. Here, $X$, $A$, and $W$ represent the state, action, and exogenous random noise processes, respectively, with $f$ denoting a known function that describes state transitions. Traditionally, the noise process $\{W_t, t \geq 0\}$ is assumed to be independent and identically distributed, with a distribution that is either fully known or can be consistently estimated. However, the occurrence of distributional shifts, typical in engineering settings, necessitates the consideration of the robustness of the policy. This paper introduces a distributionally robust stochastic control paradigm that accommodates possibly adaptive adversarial perturbation to the noise distribution within a prescribed ambiguity set. We examine two adversary models: current-action-aware and current-action-unaware, leading to different dynamic programming equations. Furthermore, we characterize the optimal finite sample minimax rates for achieving uniform learning of the robust value function across continuum states under both adversary types, considering ambiguity sets defined by $f_k$-divergence and Wasserstein distance. Finally, we demonstrate the applicability of our framework across various real-world settings.
Adaptively Learning to Select-Rank in Online Platforms
Jun 07, 2024



Abstract:Ranking algorithms are fundamental to various online platforms across e-commerce sites to content streaming services. Our research addresses the challenge of adaptively ranking items from a candidate pool for heterogeneous users, a key component in personalizing user experience. We develop a user response model that considers diverse user preferences and the varying effects of item positions, aiming to optimize overall user satisfaction with the ranked list. We frame this problem within a contextual bandits framework, with each ranked list as an action. Our approach incorporates an upper confidence bound to adjust predicted user satisfaction scores and selects the ranking action that maximizes these adjusted scores, efficiently solved via maximum weight imperfect matching. We demonstrate that our algorithm achieves a cumulative regret bound of $O(d\sqrt{NKT})$ for ranking $K$ out of $N$ items in a $d$-dimensional context space over $T$ rounds, under the assumption that user responses follow a generalized linear model. This regret alleviates dependence on the ambient action space, whose cardinality grows exponentially with $N$ and $K$ (thus rendering direct application of existing adaptive learning algorithms -- such as UCB or Thompson sampling -- infeasible). Experiments conducted on both simulated and real-world datasets demonstrate our algorithm outperforms the baseline.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge