Learning Fair Policies for Multi-stage Selection Problems from Observational Data

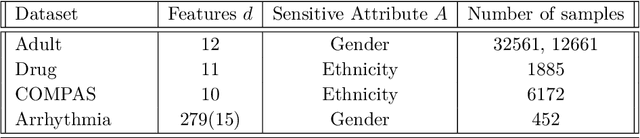
We consider the problem of learning fair policies for multi-stage selection problems from observational data. This problem arises in several high-stakes domains such as company hiring, loan approval, or bail decisions where outcomes (e.g., career success, loan repayment, recidivism) are only observed for those selected. We propose a multi-stage framework that can be augmented with various fairness constraints, such as demographic parity or equal opportunity. This problem is a highly intractable infinite chance-constrained program involving the unknown joint distribution of covariates and outcomes. Motivated by the potential impact of selection decisions on people's lives and livelihoods, we propose to focus on interpretable linear selection rules. Leveraging tools from causal inference and sample average approximation, we obtain an asymptotically consistent solution to this selection problem by solving a mixed binary conic optimization problem, which can be solved using standard off-the-shelf solvers. We conduct extensive computational experiments on a variety of datasets adapted from the UCI repository on which we show that our proposed approaches can achieve an 11.6% improvement in precision and a 38% reduction in the measure of unfairness compared to the existing selection policy.

Wasserstein Robust Support Vector Machines with Fairness Constraints

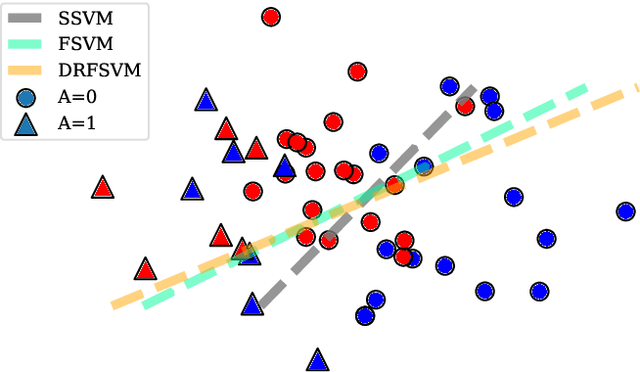
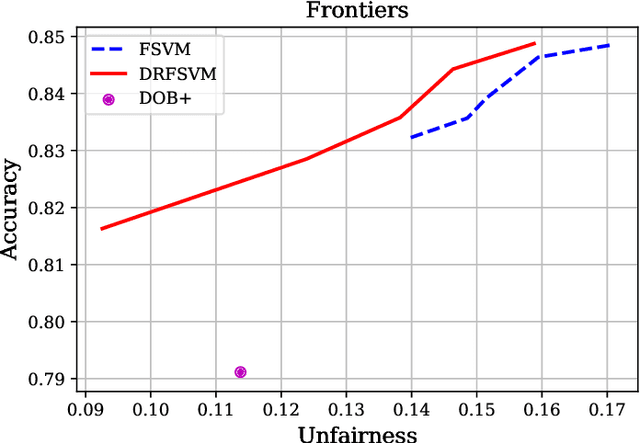
We propose a distributionally robust support vector machine with a fairness constraint that encourages the classifier to be fair in view of the equality of opportunity criterion. We use a type-$\infty$ Wasserstein ambiguity set centered at the empirical distribution to model distributional uncertainty and derive an exact reformulation for worst-case unfairness measure. We establish that the model is equivalent to a mixed-binary optimization problem, which can be solved by standard off-the-shelf solvers. We further prove that the expectation of the hinge loss objective function constitutes an upper bound on the misclassification probability. Finally, we numerically demonstrate that our proposed approach improves fairness with negligible loss of predictive accuracy.

A Robust Spectral Clustering Algorithm for Sub-Gaussian Mixture Models with Outliers

We consider the problem of clustering datasets in the presence of arbitrary outliers. Traditional clustering algorithms such as k-means and spectral clustering are known to perform poorly for datasets contaminated with even a small number of outliers. In this paper, we develop a provably robust spectral clustering algorithm that applies a simple rounding scheme to denoise a Gaussian kernel matrix built from the data points and uses vanilla spectral clustering to recover the cluster labels of data points. We analyze the performance of our algorithm under the assumption that the "good" data points are generated from a mixture of sub-gaussians (we term these "inliers"), while the outlier points can come from any arbitrary probability distribution. For this general class of models, we show that the asymptotic mis-classification error decays at an exponential rate in the signal-to-noise ratio, provided the number of outliers are a small fraction of the inlier points. Surprisingly, this derived error bound matches with the best-known bound for semidefinite programs (SDPs) under the same setting without outliers. We conduct extensive experiments on a variety of simulated and real-world datasets to demonstrate that our algorithm is less sensitive to outliers compared to other state-of-the-art algorithms proposed in the literature.