A Federated Distributionally Robust Support Vector Machine with Mixture of Wasserstein Balls Ambiguity Set for Distributed Fault Diagnosis

The training of classification models for fault diagnosis tasks using geographically dispersed data is a crucial task for original parts manufacturers (OEMs) seeking to provide long-term service contracts (LTSCs) to their customers. Due to privacy and bandwidth constraints, such models must be trained in a federated fashion. Moreover, due to harsh industrial settings the data often suffers from feature and label uncertainty. Therefore, we study the problem of training a distributionally robust (DR) support vector machine (SVM) in a federated fashion over a network comprised of a central server and $G$ clients without sharing data. We consider the setting where the local data of each client $g$ is sampled from a unique true distribution $\mathbb{P}_g$, and the clients can only communicate with the central server. We propose a novel Mixture of Wasserstein Balls (MoWB) ambiguity set that relies on local Wasserstein balls centered at the empirical distribution of the data at each client. We study theoretical aspects of the proposed ambiguity set, deriving its out-of-sample performance guarantees and demonstrating that it naturally allows for the separability of the DR problem. Subsequently, we propose two distributed optimization algorithms for training the global FDR-SVM: i) a subgradient method-based algorithm, and ii) an alternating direction method of multipliers (ADMM)-based algorithm. We derive the optimization problems to be solved by each client and provide closed-form expressions for the computations performed by the central server during each iteration for both algorithms. Finally, we thoroughly examine the performance of the proposed algorithms in a series of numerical experiments utilizing both simulation data and popular real-world datasets.

Learning Fair Policies for Multi-stage Selection Problems from Observational Data

We consider the problem of learning fair policies for multi-stage selection problems from observational data. This problem arises in several high-stakes domains such as company hiring, loan approval, or bail decisions where outcomes (e.g., career success, loan repayment, recidivism) are only observed for those selected. We propose a multi-stage framework that can be augmented with various fairness constraints, such as demographic parity or equal opportunity. This problem is a highly intractable infinite chance-constrained program involving the unknown joint distribution of covariates and outcomes. Motivated by the potential impact of selection decisions on people's lives and livelihoods, we propose to focus on interpretable linear selection rules. Leveraging tools from causal inference and sample average approximation, we obtain an asymptotically consistent solution to this selection problem by solving a mixed binary conic optimization problem, which can be solved using standard off-the-shelf solvers. We conduct extensive computational experiments on a variety of datasets adapted from the UCI repository on which we show that our proposed approaches can achieve an 11.6% improvement in precision and a 38% reduction in the measure of unfairness compared to the existing selection policy.

On the Partial Convexification for Low-Rank Spectral Optimization: Rank Bounds and Algorithms

A Low-rank Spectral Optimization Problem (LSOP) minimizes a linear objective subject to multiple two-sided linear matrix inequalities intersected with a low-rank and spectral constrained domain set. Although solving LSOP is, in general, NP-hard, its partial convexification (i.e., replacing the domain set by its convex hull) termed "LSOP-R," is often tractable and yields a high-quality solution. This motivates us to study the strength of LSOP-R. Specifically, we derive rank bounds for any extreme point of the feasible set of LSOP-R and prove their tightness for the domain sets with different matrix spaces. The proposed rank bounds recover two well-known results in the literature from a fresh angle and also allow us to derive sufficient conditions under which the relaxation LSOP-R is equivalent to the original LSOP. To effectively solve LSOP-R, we develop a column generation algorithm with a vector-based convex pricing oracle, coupled with a rank-reduction algorithm, which ensures the output solution satisfies the theoretical rank bound. Finally, we numerically verify the strength of the LSOP-R and the efficacy of the proposed algorithms.

On the Exactness of Dantzig-Wolfe Relaxation for Rank Constrained Optimization Problems

This paper studies the rank constrained optimization problem (RCOP) that aims to minimize a linear objective function over intersecting a prespecified closed rank constrained domain set with m two-sided linear constraints. Replacing the domain set by its closed convex hull offers us a convex Dantzig-Wolfe Relaxation (DWR) of the RCOP. Our goal is to characterize necessary and sufficient conditions under which the DWR and RCOP are equivalent in the sense of extreme point, convex hull, and objective value. More precisely, we develop the first-known necessary and sufficient conditions about when the DWR feasible set matches that of RCOP for any m linear constraints from two perspectives: (i) extreme point exactness -- all extreme points in the DWR feasible set belong to that of the RCOP; and (ii) convex hull exactness -- the DWR feasible set is identical to the closed convex hull of RCOP feasible set. From the optimization view, we also investigate (iii) objective exactness -- the optimal values of the DWR and RCOP coincide for any $m$ linear constraints and a family of linear objective functions. We derive the first-known necessary and sufficient conditions of objective exactness when the DWR admits four favorable classes of linear objective functions, respectively. From the primal perspective, this paper presents how our proposed conditions refine and extend the existing exactness results in the quadratically constrained quadratic program (QCQP) and fair unsupervised learning.

Smooth Robust Tensor Completion for Background/Foreground Separation with Missing Pixels: Novel Algorithm with Convergence Guarantee

The objective of this study is to address the problem of background/foreground separation with missing pixels by combining the video acquisition, video recovery, background/foreground separation into a single framework. To achieve this, a smooth robust tensor completion (SRTC) model is proposed to recover the data and decompose it into the static background and smooth foreground, respectively. Specifically, the static background is modeled by the low-rank tucker decomposition and the smooth foreground (moving objects) is modeled by the spatiotemporal continuity, which is enforced by the total variation regularization. An efficient algorithm based on tensor proximal alternating minimization (tenPAM) is implemented to solve the proposed model with global convergence guarantee under very mild conditions. Extensive experiments on real data demonstrate that the proposed method significantly outperforms the state-of-the-art approaches for background/foreground separation with missing pixels.

Unbiased Subdata Selection for Fair Classification: A Unified Framework and Scalable Algorithms

As an important problem in modern data analytics, classification has witnessed varieties of applications from different domains. Different from conventional classification approaches, fair classification concerns the issues of unintentional biases against the sensitive features (e.g., gender, race). Due to high nonconvexity of fairness measures, existing methods are often unable to model exact fairness, which can cause inferior fair classification outcomes. This paper fills the gap by developing a novel unified framework to jointly optimize accuracy and fairness. The proposed framework is versatile and can incorporate different fairness measures studied in literature precisely as well as can be applicable to many classifiers including deep classification models. Specifically, in this paper, we first prove Fisher consistency of the proposed framework. We then show that many classification models within this framework can be recast as mixed-integer convex programs, which can be solved effectively by off-the-shelf solvers when the instance sizes are moderate and can be used as benchmarks to compare the efficiency of approximation algorithms. We prove that in the proposed framework, when the classification outcomes are known, the resulting problem, termed "unbiased subdata selection," is strongly polynomial-solvable and can be used to enhance the classification fairness by selecting more representative data points. This motivates us to develop an iterative refining strategy (IRS) to solve the large-scale instances, where we improve the classification accuracy and conduct the unbiased subdata selection in an alternating fashion. We study the convergence property of IRS and derive its approximation bound. More broadly, this framework can be leveraged to improve classification models with unbalanced data by taking F1 score into consideration.

Exact and Approximation Algorithms for Sparse PCA

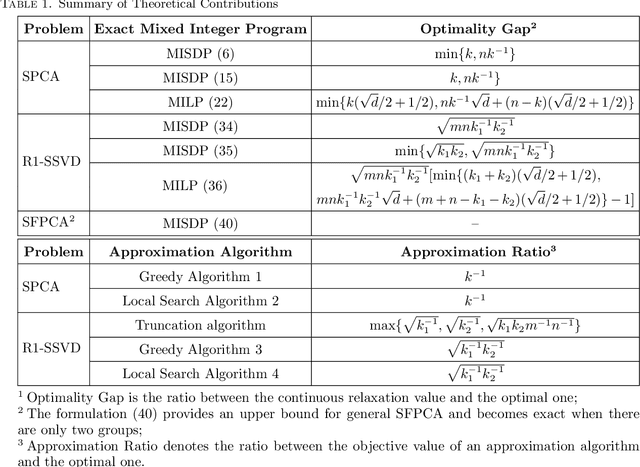
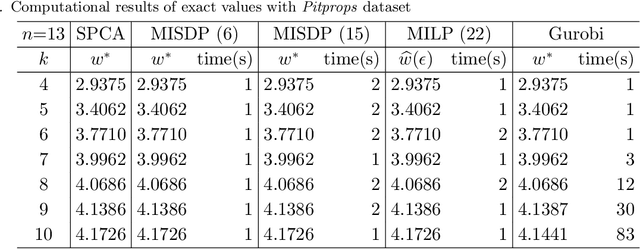
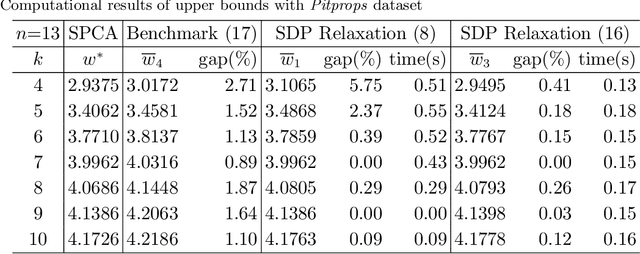
Sparse PCA (SPCA) is a fundamental model in machine learning and data analytics, which has witnessed a variety of application areas such as finance, manufacturing, biology, healthcare. To select a prespecified-size principal submatrix from a covariance matrix to maximize its largest eigenvalue for the better interpretability purpose, SPCA advances the conventional PCA with both feature selection and dimensionality reduction. This paper proposes two exact mixed-integer SDPs (MISDPs) by exploiting the spectral decomposition of the covariance matrix and the properties of the largest eigenvalues. We then analyze the theoretical optimality gaps of their continuous relaxation values and prove that they are stronger than that of the state-of-art one. We further show that the continuous relaxations of two MISDPs can be recast as saddle point problems without involving semi-definite cones, and thus can be effectively solved by first-order methods such as the subgradient method. Since off-the-shelf solvers, in general, have difficulty in solving MISDPs, we approximate SPCA with arbitrary accuracy by a mixed-integer linear program (MILP) of a similar size as MISDPs. To be more scalable, we also analyze greedy and local search algorithms, prove their first-known approximation ratios, and show that the approximation ratios are tight. Our numerical study demonstrates that the continuous relaxation values of the proposed MISDPs are quite close to optimality, the proposed MILP model can solve small and medium-size instances to optimality, and the approximation algorithms work very well for all the instances. Finally, we extend the analyses to Rank-one Sparse SVD (R1-SSVD) with non-symmetric matrices and Sparse Fair PCA (SFPCA) when there are multiple covariance matrices, each corresponding to a protected group.

Best Principal Submatrix Selection for the Maximum Entropy Sampling Problem: Scalable Algorithms and Performance Guarantees

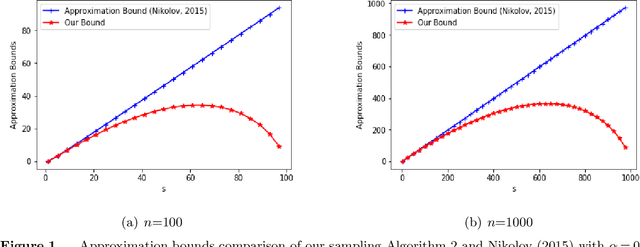
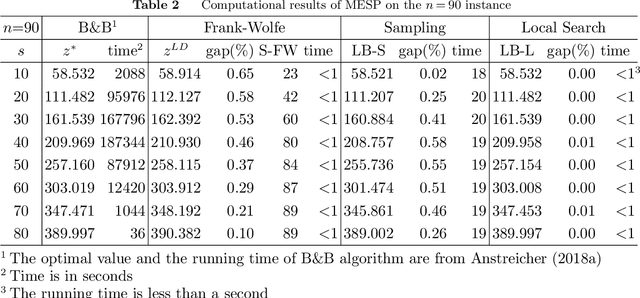
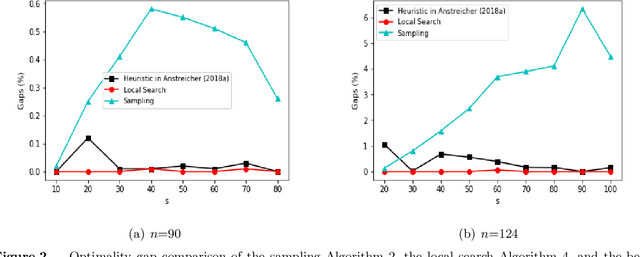
This paper studies a classic maximum entropy sampling problem (MESP), which aims to select the most informative principal submatrix of a prespecified size from a covariance matrix. MESP has been widely applied to many areas, including healthcare, power system, manufacturing and data science. By investigating its Lagrangian dual and primal characterization, we derive a novel convex integer program for MESP and show that its continuous relaxation yields a near-optimal solution. The results motivate us to study an efficient sampling algorithm and develop its approximation bound for MESP, which improves the best-known bound in literature. We then provide an efficient deterministic implementation of the sampling algorithm with the same approximation bound. By developing new mathematical tools for the singular matrices and analyzing the Lagrangian dual of the proposed convex integer program, we investigate the widely-used local search algorithm and prove its first-known approximation bound for MESP. The proof techniques further inspire us with an efficient implementation of the local search algorithm. Our numerical experiments demonstrate that these approximation algorithms can efficiently solve medium-sized and large-scale instances to near-optimality. Our proposed algorithms are coded and released as open-source software. Finally, we extend the analyses to the A-Optimal MESP (A-MESP), where the objective is to minimize the trace of the inverse of the selected principal submatrix.

Approximate Positively Correlated Distributions and Approximation Algorithms for D-optimal Design

Experimental design is a classical problem in statistics and has also found new applications in machine learning. In the experimental design problem, the aim is to estimate an unknown vector x in m-dimensions from linear measurements where a Gaussian noise is introduced in each measurement. The goal is to pick k out of the given n experiments so as to make the most accurate estimate of the unknown parameter x. Given a set S of chosen experiments, the most likelihood estimate x' can be obtained by a least squares computation. One of the robust measures of error estimation is the D-optimality criterion which aims to minimize the generalized variance of the estimator. This corresponds to minimizing the volume of the standard confidence ellipsoid for the estimation error x-x'. The problem gives rise to two natural variants depending on whether repetitions are allowed or not. The latter variant, while being more general, has also found applications in the geographical location of sensors. In this work, we first show that a 1/e-approximation for the D-optimal design problem with and without repetitions giving us the first constant factor approximation for the problem. We also consider the case when the number of experiments chosen is much larger than the dimension of the measurements and provide an asymptotically optimal approximation algorithm.