Exact and Approximation Algorithms for Sparse PCA
Paper and Code
Aug 28, 2020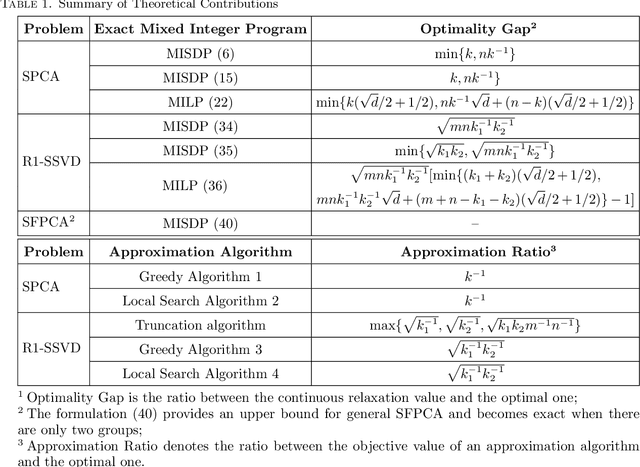
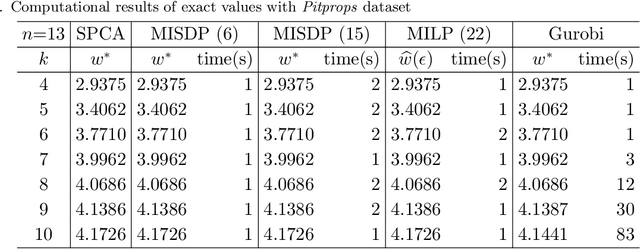
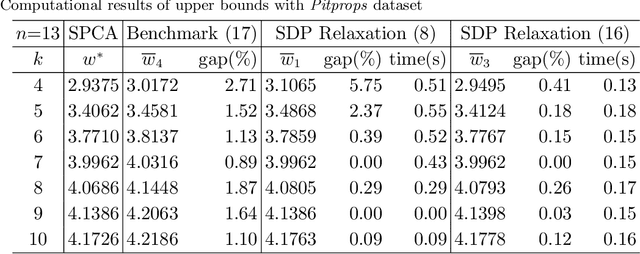
Sparse PCA (SPCA) is a fundamental model in machine learning and data analytics, which has witnessed a variety of application areas such as finance, manufacturing, biology, healthcare. To select a prespecified-size principal submatrix from a covariance matrix to maximize its largest eigenvalue for the better interpretability purpose, SPCA advances the conventional PCA with both feature selection and dimensionality reduction. This paper proposes two exact mixed-integer SDPs (MISDPs) by exploiting the spectral decomposition of the covariance matrix and the properties of the largest eigenvalues. We then analyze the theoretical optimality gaps of their continuous relaxation values and prove that they are stronger than that of the state-of-art one. We further show that the continuous relaxations of two MISDPs can be recast as saddle point problems without involving semi-definite cones, and thus can be effectively solved by first-order methods such as the subgradient method. Since off-the-shelf solvers, in general, have difficulty in solving MISDPs, we approximate SPCA with arbitrary accuracy by a mixed-integer linear program (MILP) of a similar size as MISDPs. To be more scalable, we also analyze greedy and local search algorithms, prove their first-known approximation ratios, and show that the approximation ratios are tight. Our numerical study demonstrates that the continuous relaxation values of the proposed MISDPs are quite close to optimality, the proposed MILP model can solve small and medium-size instances to optimality, and the approximation algorithms work very well for all the instances. Finally, we extend the analyses to Rank-one Sparse SVD (R1-SSVD) with non-symmetric matrices and Sparse Fair PCA (SFPCA) when there are multiple covariance matrices, each corresponding to a protected group.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge