Micro-Expression Recognition by Motion Feature Extraction based on Pre-training

Micro-expressions (MEs) are spontaneous, unconscious facial expressions that have promising applications in various fields such as psychotherapy and national security. Thus, micro-expression recognition (MER) has attracted more and more attention from researchers. Although various MER methods have emerged especially with the development of deep learning techniques, the task still faces several challenges, e.g. subtle motion and limited training data. To address these problems, we propose a novel motion extraction strategy (MoExt) for the MER task and use additional macro-expression data in the pre-training process. We primarily pretrain the feature separator and motion extractor using the contrastive loss, thus enabling them to extract representative motion features. In MoExt, shape features and texture features are first extracted separately from onset and apex frames, and then motion features related to MEs are extracted based on the shape features of both frames. To enable the model to more effectively separate features, we utilize the extracted motion features and the texture features from the onset frame to reconstruct the apex frame. Through pre-training, the module is enabled to extract inter-frame motion features of facial expressions while excluding irrelevant information. The feature separator and motion extractor are ultimately integrated into the MER network, which is then fine-tuned using the target ME data. The effectiveness of proposed method is validated on three commonly used datasets, i.e., CASME II, SMIC, SAMM, and CAS(ME)3 dataset. The results show that our method performs favorably against state-of-the-art methods.

On the Partial Convexification for Low-Rank Spectral Optimization: Rank Bounds and Algorithms

A Low-rank Spectral Optimization Problem (LSOP) minimizes a linear objective subject to multiple two-sided linear matrix inequalities intersected with a low-rank and spectral constrained domain set. Although solving LSOP is, in general, NP-hard, its partial convexification (i.e., replacing the domain set by its convex hull) termed "LSOP-R," is often tractable and yields a high-quality solution. This motivates us to study the strength of LSOP-R. Specifically, we derive rank bounds for any extreme point of the feasible set of LSOP-R and prove their tightness for the domain sets with different matrix spaces. The proposed rank bounds recover two well-known results in the literature from a fresh angle and also allow us to derive sufficient conditions under which the relaxation LSOP-R is equivalent to the original LSOP. To effectively solve LSOP-R, we develop a column generation algorithm with a vector-based convex pricing oracle, coupled with a rank-reduction algorithm, which ensures the output solution satisfies the theoretical rank bound. Finally, we numerically verify the strength of the LSOP-R and the efficacy of the proposed algorithms.

On the Exactness of Dantzig-Wolfe Relaxation for Rank Constrained Optimization Problems

This paper studies the rank constrained optimization problem (RCOP) that aims to minimize a linear objective function over intersecting a prespecified closed rank constrained domain set with m two-sided linear constraints. Replacing the domain set by its closed convex hull offers us a convex Dantzig-Wolfe Relaxation (DWR) of the RCOP. Our goal is to characterize necessary and sufficient conditions under which the DWR and RCOP are equivalent in the sense of extreme point, convex hull, and objective value. More precisely, we develop the first-known necessary and sufficient conditions about when the DWR feasible set matches that of RCOP for any m linear constraints from two perspectives: (i) extreme point exactness -- all extreme points in the DWR feasible set belong to that of the RCOP; and (ii) convex hull exactness -- the DWR feasible set is identical to the closed convex hull of RCOP feasible set. From the optimization view, we also investigate (iii) objective exactness -- the optimal values of the DWR and RCOP coincide for any $m$ linear constraints and a family of linear objective functions. We derive the first-known necessary and sufficient conditions of objective exactness when the DWR admits four favorable classes of linear objective functions, respectively. From the primal perspective, this paper presents how our proposed conditions refine and extend the existing exactness results in the quadratically constrained quadratic program (QCQP) and fair unsupervised learning.

Exact and Approximation Algorithms for Sparse PCA

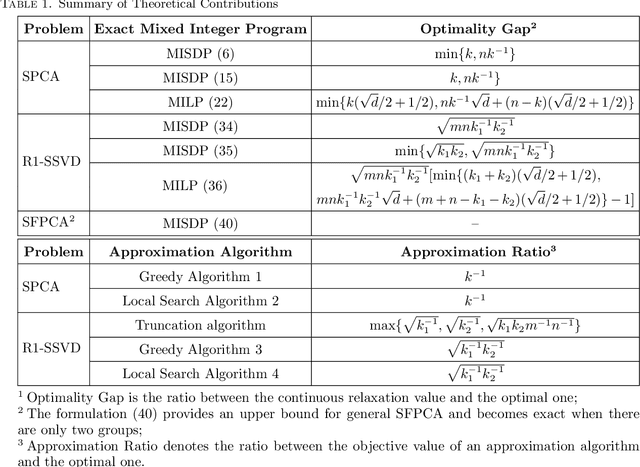
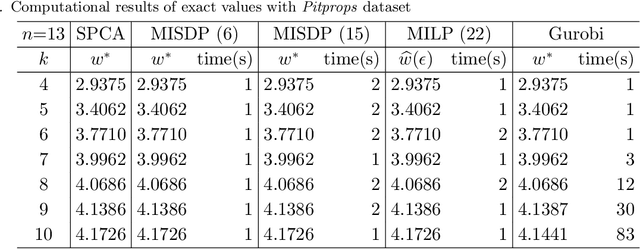
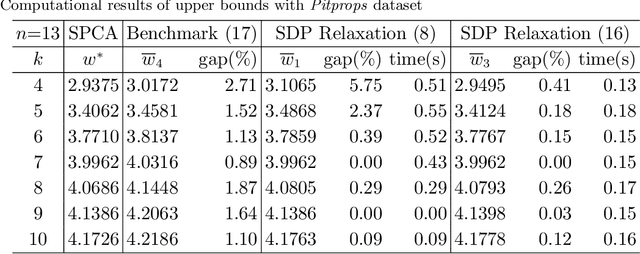
Sparse PCA (SPCA) is a fundamental model in machine learning and data analytics, which has witnessed a variety of application areas such as finance, manufacturing, biology, healthcare. To select a prespecified-size principal submatrix from a covariance matrix to maximize its largest eigenvalue for the better interpretability purpose, SPCA advances the conventional PCA with both feature selection and dimensionality reduction. This paper proposes two exact mixed-integer SDPs (MISDPs) by exploiting the spectral decomposition of the covariance matrix and the properties of the largest eigenvalues. We then analyze the theoretical optimality gaps of their continuous relaxation values and prove that they are stronger than that of the state-of-art one. We further show that the continuous relaxations of two MISDPs can be recast as saddle point problems without involving semi-definite cones, and thus can be effectively solved by first-order methods such as the subgradient method. Since off-the-shelf solvers, in general, have difficulty in solving MISDPs, we approximate SPCA with arbitrary accuracy by a mixed-integer linear program (MILP) of a similar size as MISDPs. To be more scalable, we also analyze greedy and local search algorithms, prove their first-known approximation ratios, and show that the approximation ratios are tight. Our numerical study demonstrates that the continuous relaxation values of the proposed MISDPs are quite close to optimality, the proposed MILP model can solve small and medium-size instances to optimality, and the approximation algorithms work very well for all the instances. Finally, we extend the analyses to Rank-one Sparse SVD (R1-SSVD) with non-symmetric matrices and Sparse Fair PCA (SFPCA) when there are multiple covariance matrices, each corresponding to a protected group.

Best Principal Submatrix Selection for the Maximum Entropy Sampling Problem: Scalable Algorithms and Performance Guarantees

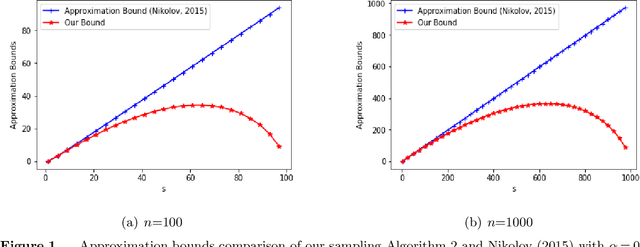
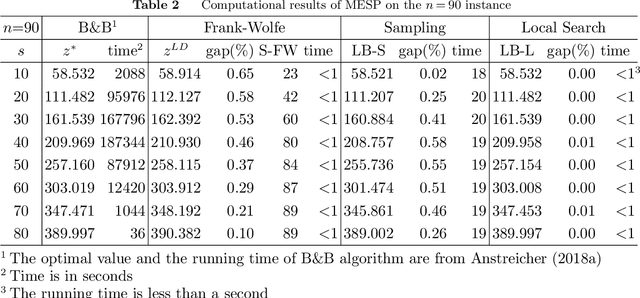
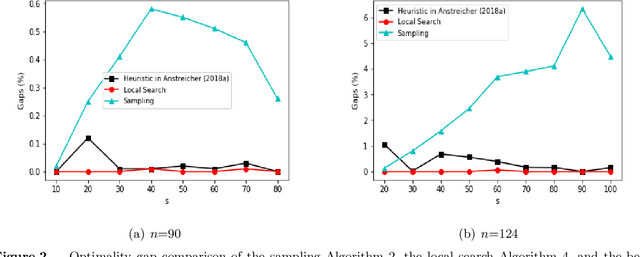
This paper studies a classic maximum entropy sampling problem (MESP), which aims to select the most informative principal submatrix of a prespecified size from a covariance matrix. MESP has been widely applied to many areas, including healthcare, power system, manufacturing and data science. By investigating its Lagrangian dual and primal characterization, we derive a novel convex integer program for MESP and show that its continuous relaxation yields a near-optimal solution. The results motivate us to study an efficient sampling algorithm and develop its approximation bound for MESP, which improves the best-known bound in literature. We then provide an efficient deterministic implementation of the sampling algorithm with the same approximation bound. By developing new mathematical tools for the singular matrices and analyzing the Lagrangian dual of the proposed convex integer program, we investigate the widely-used local search algorithm and prove its first-known approximation bound for MESP. The proof techniques further inspire us with an efficient implementation of the local search algorithm. Our numerical experiments demonstrate that these approximation algorithms can efficiently solve medium-sized and large-scale instances to near-optimality. Our proposed algorithms are coded and released as open-source software. Finally, we extend the analyses to the A-Optimal MESP (A-MESP), where the objective is to minimize the trace of the inverse of the selected principal submatrix.