Best Principal Submatrix Selection for the Maximum Entropy Sampling Problem: Scalable Algorithms and Performance Guarantees
Paper and Code
Jan 23, 2020
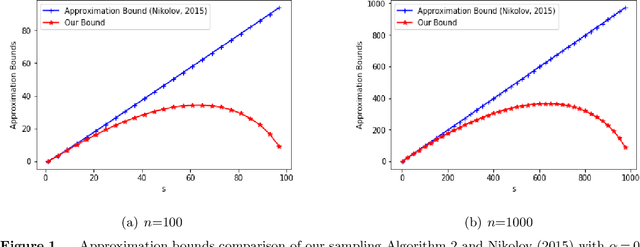
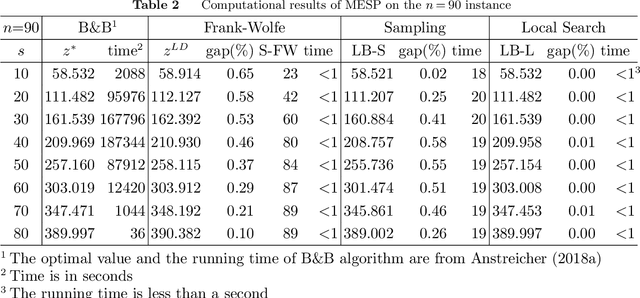
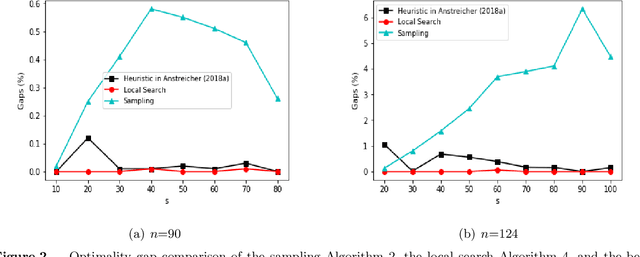
This paper studies a classic maximum entropy sampling problem (MESP), which aims to select the most informative principal submatrix of a prespecified size from a covariance matrix. MESP has been widely applied to many areas, including healthcare, power system, manufacturing and data science. By investigating its Lagrangian dual and primal characterization, we derive a novel convex integer program for MESP and show that its continuous relaxation yields a near-optimal solution. The results motivate us to study an efficient sampling algorithm and develop its approximation bound for MESP, which improves the best-known bound in literature. We then provide an efficient deterministic implementation of the sampling algorithm with the same approximation bound. By developing new mathematical tools for the singular matrices and analyzing the Lagrangian dual of the proposed convex integer program, we investigate the widely-used local search algorithm and prove its first-known approximation bound for MESP. The proof techniques further inspire us with an efficient implementation of the local search algorithm. Our numerical experiments demonstrate that these approximation algorithms can efficiently solve medium-sized and large-scale instances to near-optimality. Our proposed algorithms are coded and released as open-source software. Finally, we extend the analyses to the A-Optimal MESP (A-MESP), where the objective is to minimize the trace of the inverse of the selected principal submatrix.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge