Prognostic Framework for Robotic Manipulators Operating Under Dynamic Task Severities

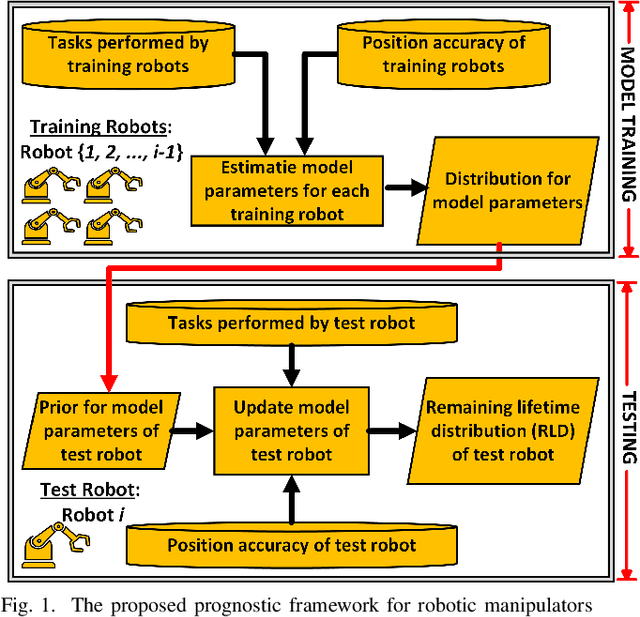
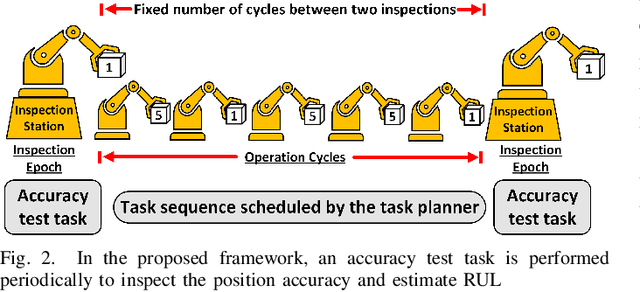
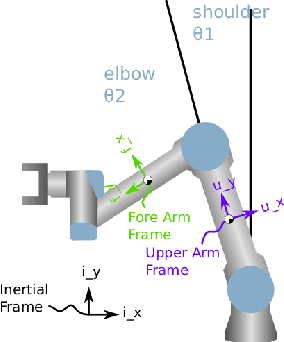
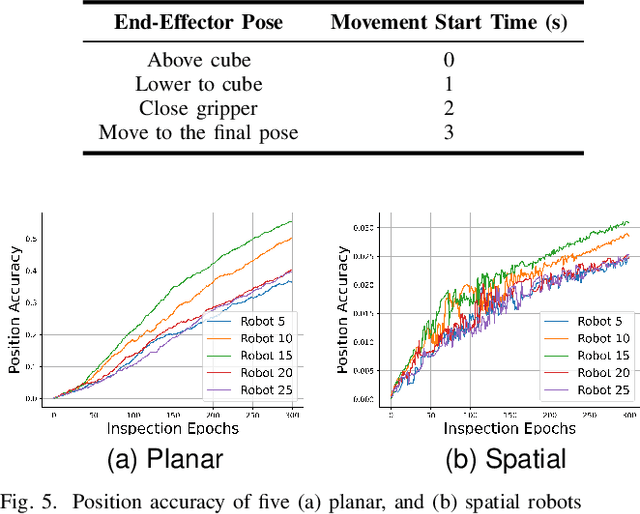
Robotic manipulators are critical in many applications but are known to degrade over time. This degradation is influenced by the nature of the tasks performed by the robot. Tasks with higher severity, such as handling heavy payloads, can accelerate the degradation process. One way this degradation is reflected is in the position accuracy of the robot's end-effector. In this paper, we present a prognostic modeling framework that predicts a robotic manipulator's Remaining Useful Life (RUL) while accounting for the effects of task severity. Our framework represents the robot's position accuracy as a Brownian motion process with a random drift parameter that is influenced by task severity. The dynamic nature of task severity is modeled using a continuous-time Markov chain (CTMC). To evaluate RUL, we discuss two approaches -- (1) a novel closed-form expression for Remaining Lifetime Distribution (RLD), and (2) Monte Carlo simulations, commonly used in prognostics literature. Theoretical results establish the equivalence between these RUL computation approaches. We validate our framework through experiments using two distinct physics-based simulators for planar and spatial robot fleets. Our findings show that robots in both fleets experience shorter RUL when handling a higher proportion of high-severity tasks.

Sensor-fusion based Prognostics Framework for Complex Engineering Systems Exhibiting Multiple Failure Modes

Complex engineering systems are often subject to multiple failure modes. Developing a remaining useful life (RUL) prediction model that does not consider the failure mode causing degradation is likely to result in inaccurate predictions. However, distinguishing between causes of failure without manually inspecting the system is nontrivial. This challenge is increased when the causes of historically observed failures are unknown. Sensors, which are useful for monitoring the state-of-health of systems, can also be used for distinguishing between multiple failure modes as the presence of multiple failure modes results in discriminatory behavior of the sensor signals. When systems are equipped with multiple sensors, some sensors may exhibit behavior correlated with degradation, while other sensors do not. Furthermore, which sensors exhibit this behavior may differ for each failure mode. In this paper, we present a simultaneous clustering and sensor selection approach for unlabeled training datasets of systems exhibiting multiple failure modes. The cluster assignments and the selected sensors are then utilized in real-time to first diagnose the active failure mode and then to predict the system RUL. We validate the complete pipeline of the methodology using a simulated dataset of systems exhibiting two failure modes and on a turbofan degradation dataset from NASA.

A Federated Distributionally Robust Support Vector Machine with Mixture of Wasserstein Balls Ambiguity Set for Distributed Fault Diagnosis

The training of classification models for fault diagnosis tasks using geographically dispersed data is a crucial task for original parts manufacturers (OEMs) seeking to provide long-term service contracts (LTSCs) to their customers. Due to privacy and bandwidth constraints, such models must be trained in a federated fashion. Moreover, due to harsh industrial settings the data often suffers from feature and label uncertainty. Therefore, we study the problem of training a distributionally robust (DR) support vector machine (SVM) in a federated fashion over a network comprised of a central server and $G$ clients without sharing data. We consider the setting where the local data of each client $g$ is sampled from a unique true distribution $\mathbb{P}_g$, and the clients can only communicate with the central server. We propose a novel Mixture of Wasserstein Balls (MoWB) ambiguity set that relies on local Wasserstein balls centered at the empirical distribution of the data at each client. We study theoretical aspects of the proposed ambiguity set, deriving its out-of-sample performance guarantees and demonstrating that it naturally allows for the separability of the DR problem. Subsequently, we propose two distributed optimization algorithms for training the global FDR-SVM: i) a subgradient method-based algorithm, and ii) an alternating direction method of multipliers (ADMM)-based algorithm. We derive the optimization problems to be solved by each client and provide closed-form expressions for the computations performed by the central server during each iteration for both algorithms. Finally, we thoroughly examine the performance of the proposed algorithms in a series of numerical experiments utilizing both simulation data and popular real-world datasets.

Deep Learning based Covert Attack Identification for Industrial Control Systems

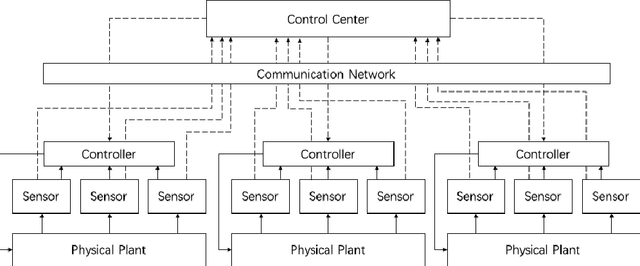
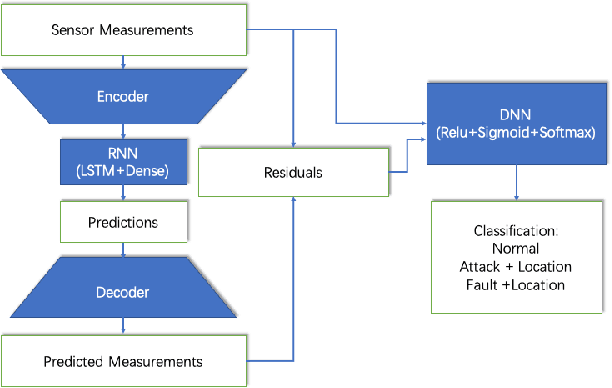
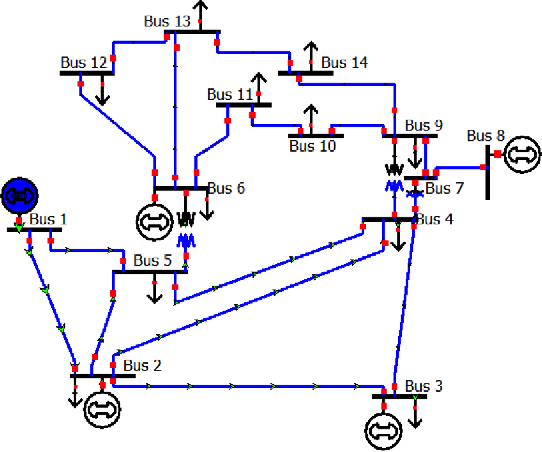
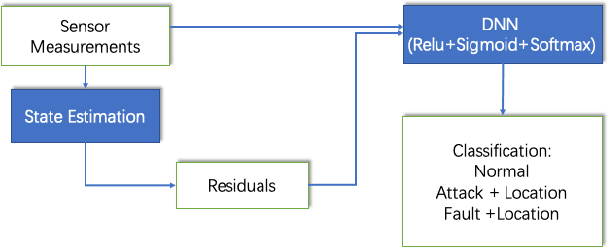
Cybersecurity of Industrial Control Systems (ICS) is drawing significant concerns as data communication increasingly leverages wireless networks. A lot of data-driven methods were developed for detecting cyberattacks, but few are focused on distinguishing them from equipment faults. In this paper, we develop a data-driven framework that can be used to detect, diagnose, and localize a type of cyberattack called covert attacks on smart grids. The framework has a hybrid design that combines an autoencoder, a recurrent neural network (RNN) with a Long-Short-Term-Memory (LSTM) layer, and a Deep Neural Network (DNN). This data-driven framework considers the temporal behavior of a generic physical system that extracts features from the time series of the sensor measurements that can be used for detecting covert attacks, distinguishing them from equipment faults, as well as localize the attack/fault. We evaluate the performance of the proposed method through a realistic simulation study on the IEEE 14-bus model as a typical example of ICS. We compare the performance of the proposed method with the traditional model-based method to show its applicability and efficacy.

Multi-Sensor Slope Change Detection

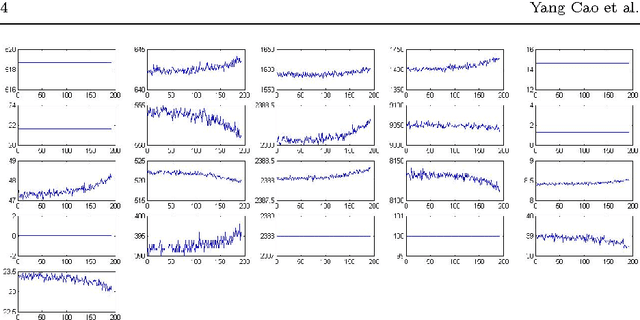
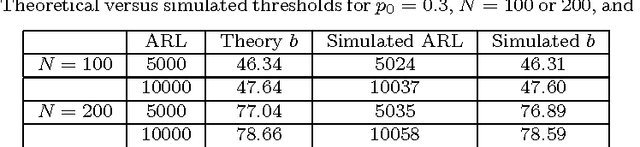
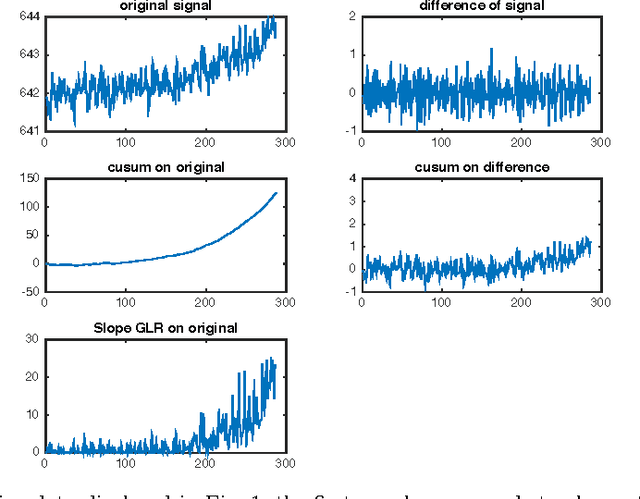
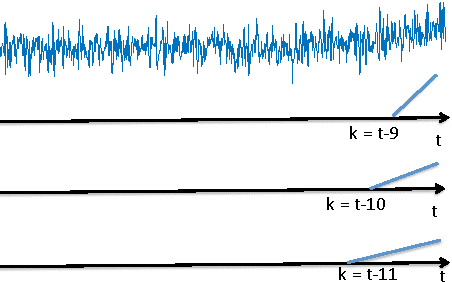
We develop a mixture procedure for multi-sensor systems to monitor data streams for a change-point that causes a gradual degradation to a subset of the streams. Observations are assumed to be initially normal random variables with known constant means and variances. After the change-point, observations in the subset will have increasing or decreasing means. The subset and the rate-of-changes are unknown. Our procedure uses a mixture statistics, which assumes that each sensor is affected by the change-point with probability $p_0$. Analytic expressions are obtained for the average run length (ARL) and the expected detection delay (EDD) of the mixture procedure, which are demonstrated to be quite accurate numerically. We establish the asymptotic optimality of the mixture procedure. Numerical examples demonstrate the good performance of the proposed procedure. We also discuss an adaptive mixture procedure using empirical Bayes. This paper extends our earlier work on detecting an abrupt change-point that causes a mean-shift, by tackling the challenges posed by the non-stationarity of the slope-change problem.