A Federated Generalized Expectation-Maximization Algorithm for Mixture Models with an Unknown Number of Components

We study the problem of federated clustering when the total number of clusters $K$ across clients is unknown, and the clients have heterogeneous but potentially overlapping cluster sets in their local data. To that end, we develop FedGEM: a federated generalized expectation-maximization algorithm for the training of mixture models with an unknown number of components. Our proposed algorithm relies on each of the clients performing EM steps locally, and constructing an uncertainty set around the maximizer associated with each local component. The central server utilizes the uncertainty sets to learn potential cluster overlaps between clients, and infer the global number of clusters via closed-form computations. We perform a thorough theoretical study of our algorithm, presenting probabilistic convergence guarantees under common assumptions. Subsequently, we study the specific setting of isotropic GMMs, providing tractable, low-complexity computations to be performed by each client during each iteration of the algorithm, as well as rigorously verifying assumptions required for algorithm convergence. We perform various numerical experiments, where we empirically demonstrate that our proposed method achieves comparable performance to centralized EM, and that it outperforms various existing federated clustering methods.

A Federated Distributionally Robust Support Vector Machine with Mixture of Wasserstein Balls Ambiguity Set for Distributed Fault Diagnosis

The training of classification models for fault diagnosis tasks using geographically dispersed data is a crucial task for original parts manufacturers (OEMs) seeking to provide long-term service contracts (LTSCs) to their customers. Due to privacy and bandwidth constraints, such models must be trained in a federated fashion. Moreover, due to harsh industrial settings the data often suffers from feature and label uncertainty. Therefore, we study the problem of training a distributionally robust (DR) support vector machine (SVM) in a federated fashion over a network comprised of a central server and $G$ clients without sharing data. We consider the setting where the local data of each client $g$ is sampled from a unique true distribution $\mathbb{P}_g$, and the clients can only communicate with the central server. We propose a novel Mixture of Wasserstein Balls (MoWB) ambiguity set that relies on local Wasserstein balls centered at the empirical distribution of the data at each client. We study theoretical aspects of the proposed ambiguity set, deriving its out-of-sample performance guarantees and demonstrating that it naturally allows for the separability of the DR problem. Subsequently, we propose two distributed optimization algorithms for training the global FDR-SVM: i) a subgradient method-based algorithm, and ii) an alternating direction method of multipliers (ADMM)-based algorithm. We derive the optimization problems to be solved by each client and provide closed-form expressions for the computations performed by the central server during each iteration for both algorithms. Finally, we thoroughly examine the performance of the proposed algorithms in a series of numerical experiments utilizing both simulation data and popular real-world datasets.

The CausalBench challenge: A machine learning contest for gene network inference from single-cell perturbation data

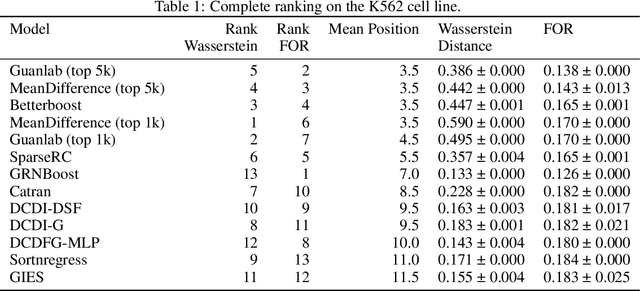
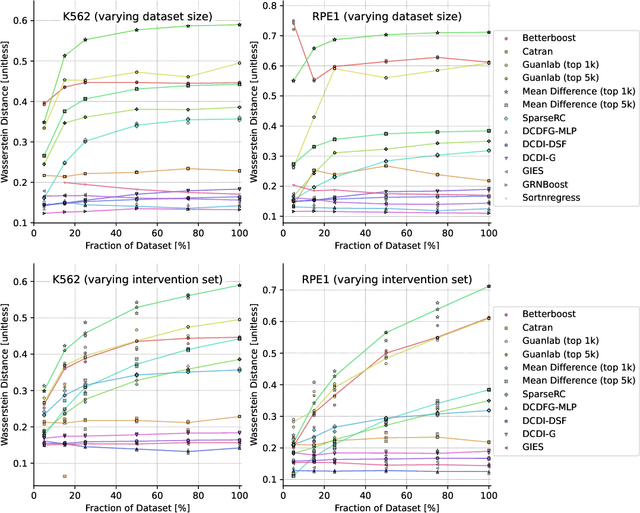
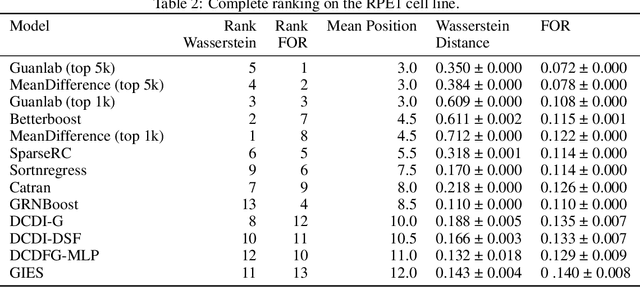
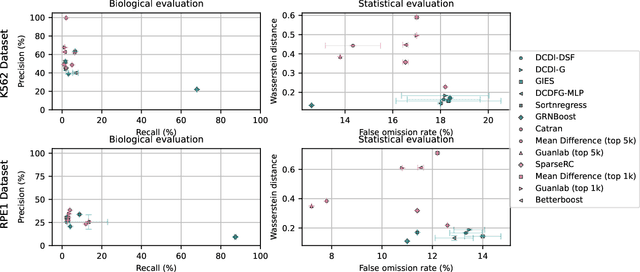
In drug discovery, mapping interactions between genes within cellular systems is a crucial early step. This helps formulate hypotheses regarding molecular mechanisms that could potentially be targeted by future medicines. The CausalBench Challenge was an initiative to invite the machine learning community to advance the state of the art in constructing gene-gene interaction networks. These networks, derived from large-scale, real-world datasets of single cells under various perturbations, are crucial for understanding the causal mechanisms underlying disease biology. Using the framework provided by the CausalBench benchmark, participants were tasked with enhancing the capacity of the state of the art methods to leverage large-scale genetic perturbation data. This report provides an analysis and summary of the methods submitted during the challenge to give a partial image of the state of the art at the time of the challenge. The winning solutions significantly improved performance compared to previous baselines, establishing a new state of the art for this critical task in biology and medicine.