Distributionally Robust Policy Learning under Concept Drifts

Distributionally robust policy learning aims to find a policy that performs well under the worst-case distributional shift, and yet most existing methods for robust policy learning consider the worst-case joint distribution of the covariate and the outcome. The joint-modeling strategy can be unnecessarily conservative when we have more information on the source of distributional shifts. This paper studiesa more nuanced problem -- robust policy learning under the concept drift, when only the conditional relationship between the outcome and the covariate changes. To this end, we first provide a doubly-robust estimator for evaluating the worst-case average reward of a given policy under a set of perturbed conditional distributions. We show that the policy value estimator enjoys asymptotic normality even if the nuisance parameters are estimated with a slower-than-root-$n$ rate. We then propose a learning algorithm that outputs the policy maximizing the estimated policy value within a given policy class $\Pi$, and show that the sub-optimality gap of the proposed algorithm is of the order $\kappa(\Pi)n^{-1/2}$, with $\kappa(\Pi)$ is the entropy integral of $\Pi$ under the Hamming distance and $n$ is the sample size. A matching lower bound is provided to show the optimality of the rate. The proposed methods are implemented and evaluated in numerical studies, demonstrating substantial improvement compared with existing benchmarks.

Conformal Alignment: Knowing When to Trust Foundation Models with Guarantees

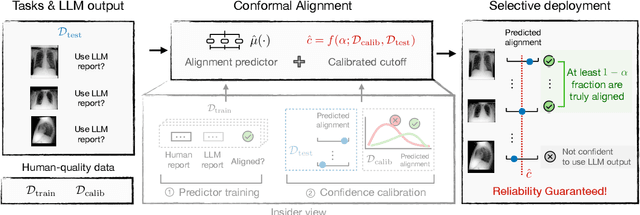
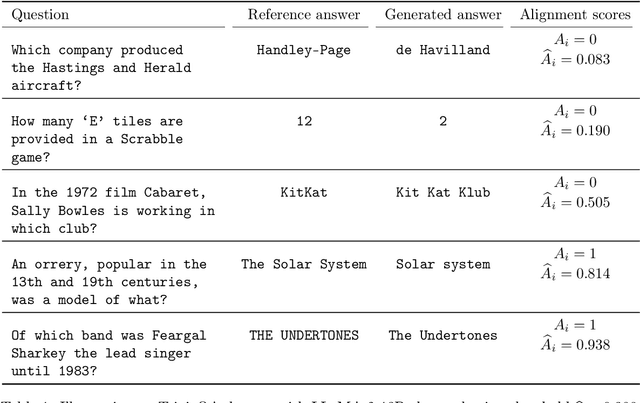
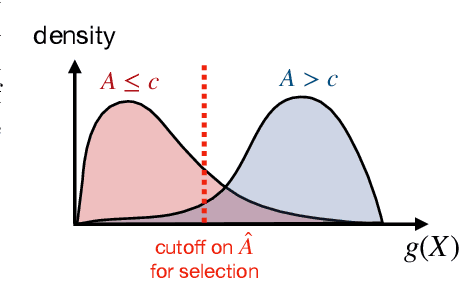
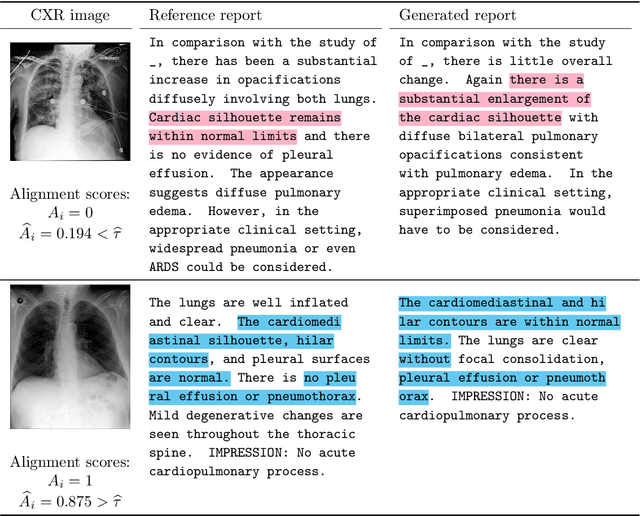
Before deploying outputs from foundation models in high-stakes tasks, it is imperative to ensure that they align with human values. For instance, in radiology report generation, reports generated by a vision-language model must align with human evaluations before their use in medical decision-making. This paper presents Conformal Alignment, a general framework for identifying units whose outputs meet a user-specified alignment criterion. It is guaranteed that on average, a prescribed fraction of selected units indeed meet the alignment criterion, regardless of the foundation model or the data distribution. Given any pre-trained model and new units with model-generated outputs, Conformal Alignment leverages a set of reference data with ground-truth alignment status to train an alignment predictor. It then selects new units whose predicted alignment scores surpass a data-dependent threshold, certifying their corresponding outputs as trustworthy. Through applications to question answering and radiology report generation, we demonstrate that our method is able to accurately identify units with trustworthy outputs via lightweight training over a moderate amount of reference data. En route, we investigate the informativeness of various features in alignment prediction and combine them with standard models to construct the alignment predictor.

Confidence on the Focal: Conformal Prediction with Selection-Conditional Coverage

Conformal prediction builds marginally valid prediction intervals which cover the unknown outcome of a randomly drawn new test point with a prescribed probability. In practice, a common scenario is that, after seeing the test unit(s), practitioners decide which test unit(s) to focus on in a data-driven manner, and wish to quantify the uncertainty for the focal unit(s). In such cases, marginally valid prediction intervals for these focal units can be misleading due to selection bias. This paper presents a general framework for constructing a prediction set with finite-sample exact coverage conditional on the unit being selected. Its general form works for arbitrary selection rules, and generalizes Mondrian Conformal Prediction to multiple test units and non-equivariant classifiers. We then work out computationally efficient implementation of our framework for a number of realistic selection rules, including top-K selection, optimization-based selection, selection based on conformal p-values, and selection based on properties of preliminary conformal prediction sets. The performance of our methods is demonstrated via applications in drug discovery and health risk prediction.

Iterative Approximate Cross-Validation

Cross-validation (CV) is one of the most popular tools for assessing and selecting predictive models. However, standard CV suffers from high computational cost when the number of folds is large. Recently, under the empirical risk minimization (ERM) framework, a line of works proposed efficient methods to approximate CV based on the solution of the ERM problem trained on the full dataset. However, in large-scale problems, it can be hard to obtain the exact solution of the ERM problem, either due to limited computational resources or due to early stopping as a way of preventing overfitting. In this paper, we propose a new paradigm to efficiently approximate CV when the ERM problem is solved via an iterative first-order algorithm, without running until convergence. Our new method extends existing guarantees for CV approximation to hold along the whole trajectory of the algorithm, including at convergence, thus generalizing existing CV approximation methods. Finally, we illustrate the accuracy and computational efficiency of our method through a range of empirical studies.

Policy learning "without'' overlap: Pessimism and generalized empirical Bernstein's inequality

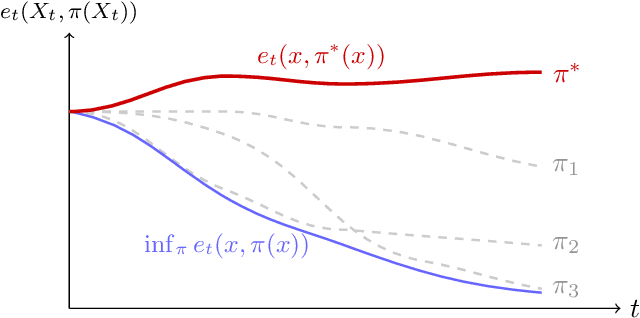
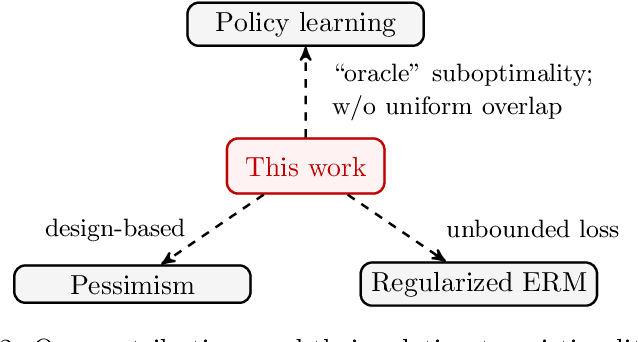
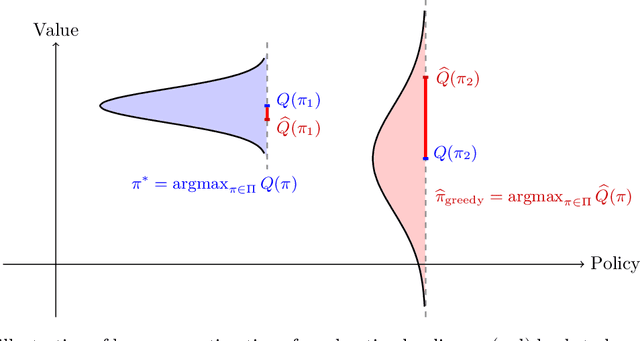
This paper studies offline policy learning, which aims at utilizing observations collected a priori (from either fixed or adaptively evolving behavior policies) to learn an optimal individualized decision rule that achieves the best overall outcomes for a given population. Existing policy learning methods rely on a uniform overlap assumption, i.e., the propensities of exploring all actions for all individual characteristics are lower bounded in the offline dataset; put differently, the performance of the existing methods depends on the worst-case propensity in the offline dataset. As one has no control over the data collection process, this assumption can be unrealistic in many situations, especially when the behavior policies are allowed to evolve over time with diminishing propensities for certain actions. In this paper, we propose a new algorithm that optimizes lower confidence bounds (LCBs) -- instead of point estimates -- of the policy values. The LCBs are constructed using knowledge of the behavior policies for collecting the offline data. Without assuming any uniform overlap condition, we establish a data-dependent upper bound for the suboptimality of our algorithm, which only depends on (i) the overlap for the optimal policy, and (ii) the complexity of the policy class we optimize over. As an implication, for adaptively collected data, we ensure efficient policy learning as long as the propensities for optimal actions are lower bounded over time, while those for suboptimal ones are allowed to diminish arbitrarily fast. In our theoretical analysis, we develop a new self-normalized type concentration inequality for inverse-propensity-weighting estimators, generalizing the well-known empirical Bernstein's inequality to unbounded and non-i.i.d. data.

Policy Learning with Adaptively Collected Data

Learning optimal policies from historical data enables the gains from personalization to be realized in a wide variety of applications. The growing policy learning literature focuses on a setting where the treatment assignment policy does not adapt to the data. However, adaptive data collection is becoming more common in practice, from two primary sources: 1) data collected from adaptive experiments that are designed to improve inferential efficiency; 2) data collected from production systems that are adaptively evolving an operational policy to improve performance over time (e.g. contextual bandits). In this paper, we aim to address the challenge of learning the optimal policy with adaptively collected data and provide one of the first theoretical inquiries into this problem. We propose an algorithm based on generalized augmented inverse propensity weighted estimators and establish its finite-sample regret bound. We complement this regret upper bound with a lower bound that characterizes the fundamental difficulty of policy learning with adaptive data. Finally, we demonstrate our algorithm's effectiveness using both synthetic data and public benchmark datasets.

Conformalized Survival Analysis

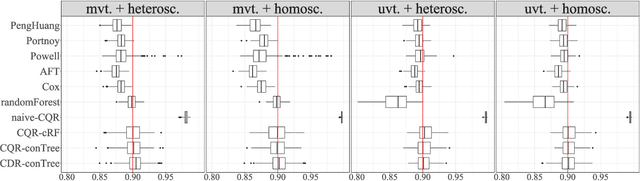
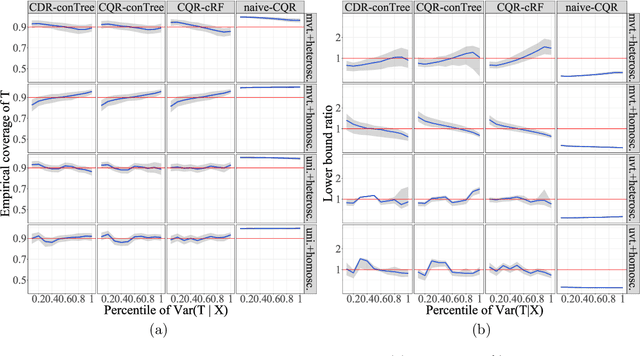
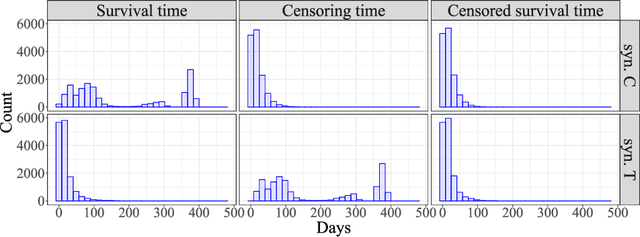
Existing survival analysis techniques heavily rely on strong modelling assumptions and are, therefore, prone to model misspecification errors. In this paper, we develop an inferential method based on ideas from conformal prediction, which can wrap around any survival prediction algorithm to produce calibrated, covariate-dependent lower predictive bounds on survival times. In the Type I right-censoring setting, when the censoring times are completely exogenous, the lower predictive bounds have guaranteed coverage in finite samples without any assumptions other than that of operating on independent and identically distributed data points. Under a more general conditionally independent censoring assumption, the bounds satisfy a doubly robust property which states the following: marginal coverage is approximately guaranteed if either the censoring mechanism or the conditional survival function is estimated well. Further, we demonstrate that the lower predictive bounds remain valid and informative for other types of censoring. The validity and efficiency of our procedure are demonstrated on synthetic data and real COVID-19 data from the UK Biobank.

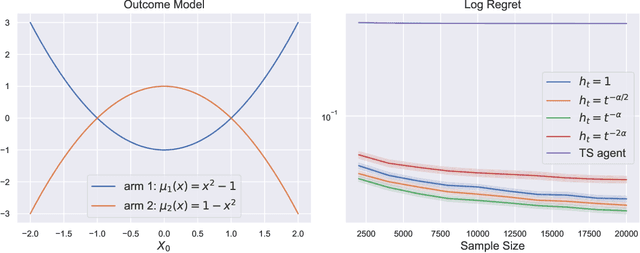
Doubly-Adaptive Thompson Sampling for Multi-Armed and Contextual Bandits

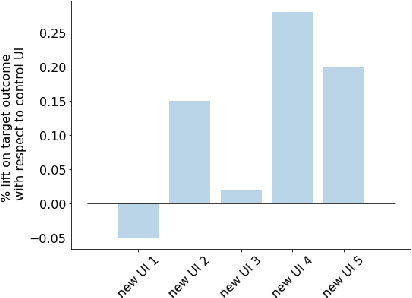
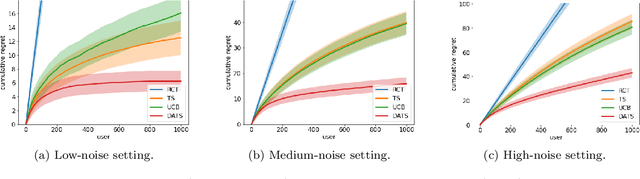
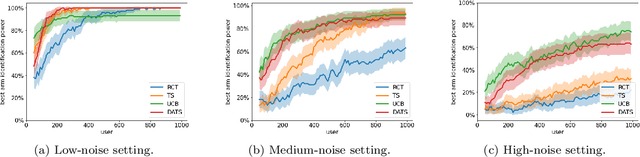
To balance exploration and exploitation, multi-armed bandit algorithms need to conduct inference on the true mean reward of each arm in every time step using the data collected so far. However, the history of arms and rewards observed up to that time step is adaptively collected and there are known challenges in conducting inference with non-iid data. In particular, sample averages, which play a prominent role in traditional upper confidence bound algorithms and traditional Thompson sampling algorithms, are neither unbiased nor asymptotically normal. We propose a variant of a Thompson sampling based algorithm that leverages recent advances in the causal inference literature and adaptively re-weighs the terms of a doubly robust estimator on the true mean reward of each arm -- hence its name doubly-adaptive Thompson sampling. The regret of the proposed algorithm matches the optimal (minimax) regret rate and its empirical evaluation in a semi-synthetic experiment based on data from a randomized control trial of a web service is performed: we see that the proposed doubly-adaptive Thompson sampling has superior empirical performance to existing baselines in terms of cumulative regret and statistical power in identifying the best arm. Further, we extend this approach to contextual bandits, where there are more sources of bias present apart from the adaptive data collection -- such as the mismatch between the true data generating process and the reward model assumptions or the unequal representations of certain regions of the context space in initial stages of learning -- and propose the linear contextual doubly-adaptive Thompson sampling and the non-parametric contextual doubly-adaptive Thompson sampling extensions of our approach.

Dynamic Batch Learning in High-Dimensional Sparse Linear Contextual Bandits

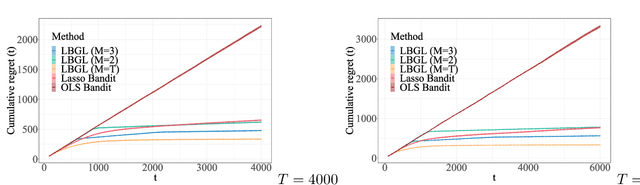
We study the problem of dynamic batch learning in high-dimensional sparse linear contextual bandits, where a decision maker, under a given maximum-number-of-batch constraint and only able to observe rewards at the end of each batch, can dynamically decide how many individuals to include in the next batch (at the end of the current batch) and what personalized action-selection scheme to adopt within each batch. Such batch constraints are ubiquitous in a variety of practical contexts, including personalized product offerings in marketing and medical treatment selection in clinical trials. We characterize the fundamental learning limit in this problem via a regret lower bound and provide a matching upper bound (up to log factors), thus prescribing an optimal scheme for this problem. To the best of our knowledge, our work provides the first inroad into a theoretical understanding of dynamic batch learning in high-dimensional sparse linear contextual bandits. Notably, even a special case of our result (when no batch constraint is present) yields the first minimax optimal $\tilde{O}(\sqrt{s_0T})$ regret bound for standard online learning in high-dimensional linear contextual bandits (for the no-margin case), where $s_0$ is the sparsity parameter (or an upper bound thereof) and $T$ is the learning horizon. This result (both that $\tilde{O}(\sqrt{s_0 T})$ is achievable and that $\Omega(\sqrt{s_0 T})$ is a lower bound) appears to be unknown in the emerging literature of high-dimensional contextual bandits.

Batched Multi-armed Bandits Problem

In this paper, we study the multi-armed bandit problem in the batched setting where the employed policy must split data into a small number of batches. While the minimax regret for the two-armed stochastic bandits has been completely characterized in \cite{perchet2016batched}, the effect of the number of arms on the regret for the multi-armed case is still open. Moreover, the question whether adaptively chosen batch sizes will help to reduce the regret also remains underexplored. In this paper, we propose the BaSE (batched successive elimination) policy to achieve the rate-optimal regret (within logarithmic factors) for batched multi-armed bandits, with matching lower bounds even if the batch sizes are determined in a data-driven manner.