Statistical Inference under Performativity

Performativity of predictions refers to the phenomena that prediction-informed decisions may influence the target they aim to predict, which is widely observed in policy-making in social sciences and economics. In this paper, we initiate the study of statistical inference under performativity. Our contribution is two-fold. First, we build a central limit theorem for estimation and inference under performativity, which enables inferential purposes in policy-making such as constructing confidence intervals or testing hypotheses. Second, we further leverage the derived central limit theorem to investigate prediction-powered inference (PPI) under performativity, which is based on a small labeled dataset and a much larger dataset of machine-learning predictions. This enables us to obtain more precise estimation and improved confidence regions for the model parameter (i.e., policy) of interest in performative prediction. We demonstrate the power of our framework by numerical experiments. To the best of our knowledge, this paper is the first one to establish statistical inference under performativity, which brings up new challenges and inference settings that we believe will add significant values to policy-making, statistics, and machine learning.

Conformal Tail Risk Control for Large Language Model Alignment

Recent developments in large language models (LLMs) have led to their widespread usage for various tasks. The prevalence of LLMs in society implores the assurance on the reliability of their performance. In particular, risk-sensitive applications demand meticulous attention to unexpectedly poor outcomes, i.e., tail events, for instance, toxic answers, humiliating language, and offensive outputs. Due to the costly nature of acquiring human annotations, general-purpose scoring models have been created to automate the process of quantifying these tail events. This phenomenon introduces potential human-machine misalignment between the respective scoring mechanisms. In this work, we present a lightweight calibration framework for blackbox models that ensures the alignment of humans and machines with provable guarantees. Our framework provides a rigorous approach to controlling any distortion risk measure that is characterized by a weighted average of quantiles of the loss incurred by the LLM with high confidence. The theoretical foundation of our method relies on the connection between conformal risk control and a traditional family of statistics, i.e., L-statistics. To demonstrate the utility of our framework, we conduct comprehensive experiments that address the issue of human-machine misalignment.

Predictions as Surrogates: Revisiting Surrogate Outcomes in the Age of AI

We establish a formal connection between the decades-old surrogate outcome model in biostatistics and economics and the emerging field of prediction-powered inference (PPI). The connection treats predictions from pre-trained models, prevalent in the age of AI, as cost-effective surrogates for expensive outcomes. Building on the surrogate outcomes literature, we develop recalibrated prediction-powered inference, a more efficient approach to statistical inference than existing PPI proposals. Our method departs from the existing proposals by using flexible machine learning techniques to learn the optimal ``imputed loss'' through a step we call recalibration. Importantly, the method always improves upon the estimator that relies solely on the data with available true outcomes, even when the optimal imputed loss is estimated imperfectly, and it achieves the smallest asymptotic variance among PPI estimators if the estimate is consistent. Computationally, our optimization objective is convex whenever the loss function that defines the target parameter is convex. We further analyze the benefits of recalibration, both theoretically and numerically, in several common scenarios where machine learning predictions systematically deviate from the outcome of interest. We demonstrate significant gains in effective sample size over existing PPI proposals via three applications leveraging state-of-the-art machine learning/AI models.

Bellman Conformal Inference: Calibrating Prediction Intervals For Time Series

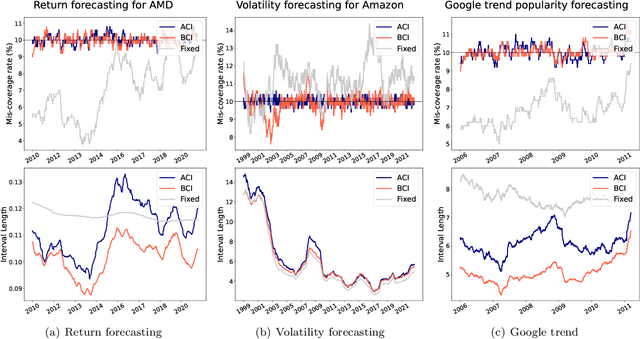
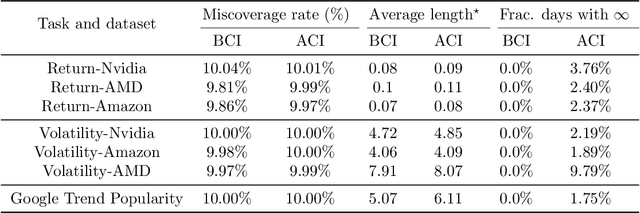
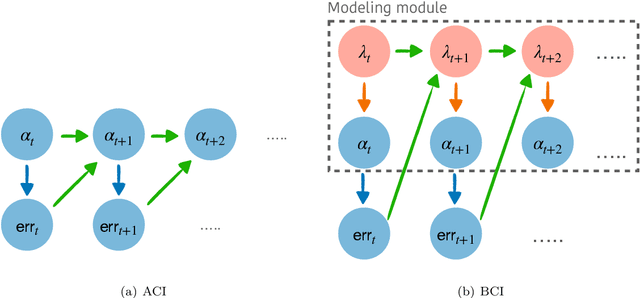
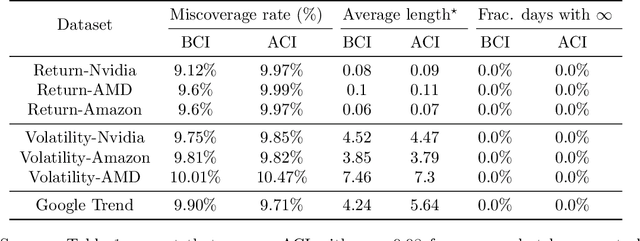
We introduce Bellman Conformal Inference (BCI), a framework that wraps around any time series forecasting models and provides approximately calibrated prediction intervals. Unlike existing methods, BCI is able to leverage multi-step ahead forecasts and explicitly optimize the average interval lengths by solving a one-dimensional stochastic control problem (SCP) at each time step. In particular, we use the dynamic programming algorithm to find the optimal policy for the SCP. We prove that BCI achieves long-term coverage under arbitrary distribution shifts and temporal dependence, even with poor multi-step ahead forecasts. We find empirically that BCI avoids uninformative intervals that have infinite lengths and generates substantially shorter prediction intervals in multiple applications when compared with existing methods.

Model-Agnostic Covariate-Assisted Inference on Partially Identified Causal Effects

Many causal estimands are only partially identifiable since they depend on the unobservable joint distribution between potential outcomes. Stratification on pretreatment covariates can yield sharper partial identification bounds; however, unless the covariates are discrete with relatively small support, this approach typically requires consistent estimation of the conditional distributions of the potential outcomes given the covariates. Thus, existing approaches may fail under model misspecification or if consistency assumptions are violated. In this study, we propose a unified and model-agnostic inferential approach for a wide class of partially identified estimands, based on duality theory for optimal transport problems. In randomized experiments, our approach can wrap around any estimates of the conditional distributions and provide uniformly valid inference, even if the initial estimates are arbitrarily inaccurate. Also, our approach is doubly robust in observational studies. Notably, this property allows analysts to use the multiplier bootstrap to select covariates and models without sacrificing validity even if the true model is not included. Furthermore, if the conditional distributions are estimated at semiparametric rates, our approach matches the performance of an oracle with perfect knowledge of the outcome model. Finally, we propose an efficient computational framework, enabling implementation on many practical problems in causal inference.

Learning from a Biased Sample

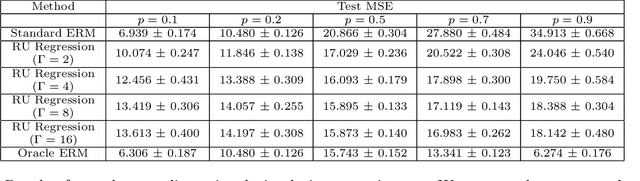
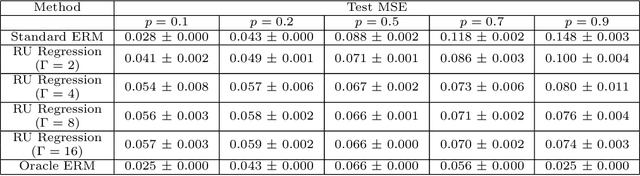
The empirical risk minimization approach to data-driven decision making assumes that we can learn a decision rule from training data drawn under the same conditions as the ones we want to deploy it under. However, in a number of settings, we may be concerned that our training sample is biased, and that some groups (characterized by either observable or unobservable attributes) may be under- or over-represented relative to the general population; and in this setting empirical risk minimization over the training set may fail to yield rules that perform well at deployment. Building on concepts from distributionally robust optimization and sensitivity analysis, we propose a method for learning a decision rule that minimizes the worst-case risk incurred under a family of test distributions whose conditional distributions of outcomes $Y$ given covariates $X$ differ from the conditional training distribution by at most a constant factor, and whose covariate distributions are absolutely continuous with respect to the covariate distribution of the training data. We apply a result of Rockafellar and Uryasev to show that this problem is equivalent to an augmented convex risk minimization problem. We give statistical guarantees for learning a robust model using the method of sieves and propose a deep learning algorithm whose loss function captures our robustness target. We empirically validate our proposed method in simulations and a case study with the MIMIC-III dataset.

Machine learning meets false discovery rate

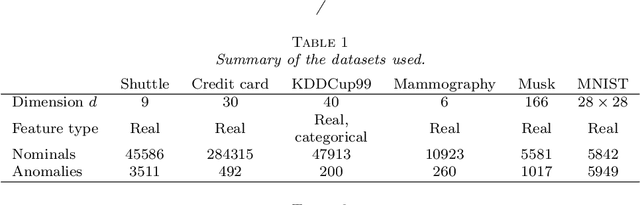
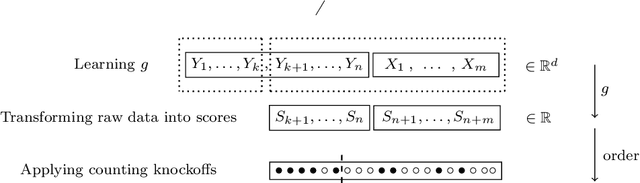
Classical false discovery rate (FDR) controlling procedures offer strong and interpretable guarantees, while they often lack of flexibility. On the other hand, recent machine learning classification algorithms, as those based on random forests (RF) or neural networks (NN), have great practical performances but lack of interpretation and of theoretical guarantees. In this paper, we make these two meet by introducing a new adaptive novelty detection procedure with FDR control, called AdaDetect. It extends the scope of recent works of multiple testing literature to the high dimensional setting, notably the one in Yang et al. (2021). AdaDetect is shown to both control strongly the FDR and to have a power that mimics the one of the oracle in a specific sense. The interest and validity of our approach is demonstrated with theoretical results, numerical experiments on several benchmark datasets and with an application to astrophysical data. In particular, while AdaDetect can be used in combination with any classifier, it is particularly efficient on real-world datasets with RF, and on images with NN.

Conformal Risk Control

We extend conformal prediction to control the expected value of any monotone loss function. The algorithm generalizes split conformal prediction together with its coverage guarantee. Like conformal prediction, the conformal risk control procedure is tight up to an $\mathcal{O}(1/n)$ factor. Worked examples from computer vision and natural language processing demonstrate the usage of our algorithm to bound the false negative rate, graph distance, and token-level F1-score.

Learn then Test: Calibrating Predictive Algorithms to Achieve Risk Control

We introduce Learn then Test, a framework for calibrating machine learning models so that their predictions satisfy explicit, finite-sample statistical guarantees regardless of the underlying model and (unknown) data-generating distribution. The framework addresses, among other examples, false discovery rate control in multi-label classification, intersection-over-union control in instance segmentation, and the simultaneous control of the type-1 error of outlier detection and confidence set coverage in classification or regression. To accomplish this, we solve a key technical challenge: the control of arbitrary risks that are not necessarily monotonic. Our main insight is to reframe the risk-control problem as multiple hypothesis testing, enabling techniques and mathematical arguments different from those in the previous literature. We use our framework to provide new calibration methods for several core machine learning tasks with detailed worked examples in computer vision.

Testing for Outliers with Conformal p-values

This paper studies the construction of p-values for nonparametric outlier detection, taking a multiple-testing perspective. The goal is to test whether new independent samples belong to the same distribution as a reference data set or are outliers. We propose a solution based on conformal inference, a broadly applicable framework which yields p-values that are marginally valid but mutually dependent for different test points. We prove these p-values are positively dependent and enable exact false discovery rate control, although in a relatively weak marginal sense. We then introduce a new method to compute p-values that are both valid conditionally on the training data and independent of each other for different test points; this paves the way to stronger type-I error guarantees. Our results depart from classical conformal inference as we leverage concentration inequalities rather than combinatorial arguments to establish our finite-sample guarantees. Furthermore, our techniques also yield a uniform confidence bound for the false positive rate of any outlier detection algorithm, as a function of the threshold applied to its raw statistics. Finally, the relevance of our results is demonstrated by numerical experiments on real and simulated data.