Synthetic continued pretraining

Pretraining on large-scale, unstructured internet text has enabled language models to acquire a significant amount of world knowledge. However, this knowledge acquisition is data-inefficient -- to learn a given fact, models must be trained on hundreds to thousands of diverse representations of it. This poses a challenge when adapting a pretrained model to a small corpus of domain-specific documents, where each fact may appear rarely or only once. We propose to bridge this gap with synthetic continued pretraining: using the small domain-specific corpus to synthesize a large corpus more amenable to learning, and then performing continued pretraining on the synthesized corpus. We instantiate this proposal with EntiGraph, a synthetic data augmentation algorithm that extracts salient entities from the source documents and then generates diverse text by drawing connections between the sampled entities. Synthetic continued pretraining using EntiGraph enables a language model to answer questions and follow generic instructions related to the source documents without access to them. If instead, the source documents are available at inference time, we show that the knowledge acquired through our approach compounds with retrieval-augmented generation. To better understand these results, we build a simple mathematical model of EntiGraph, and show how synthetic data augmentation can "rearrange" knowledge to enable more data-efficient learning.

Bellman Conformal Inference: Calibrating Prediction Intervals For Time Series

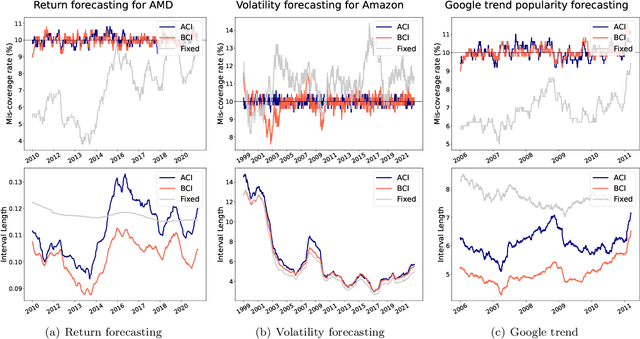
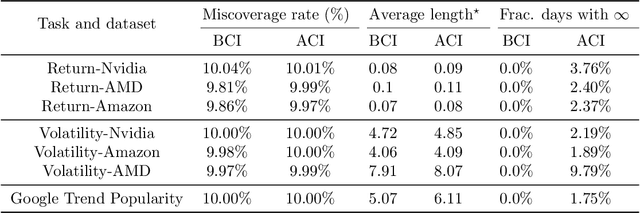
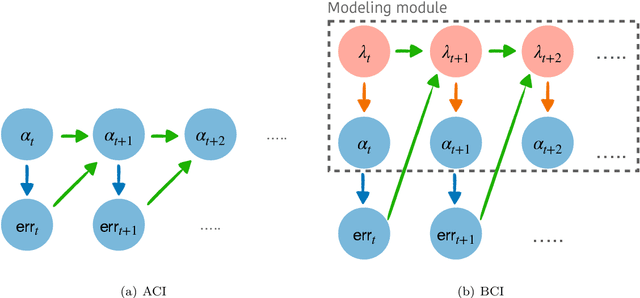
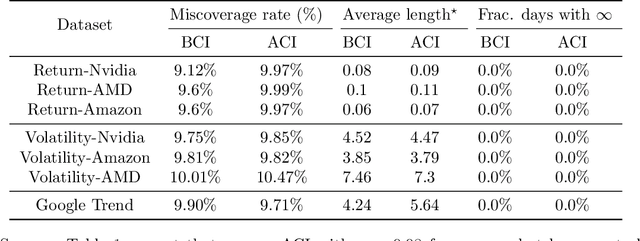
We introduce Bellman Conformal Inference (BCI), a framework that wraps around any time series forecasting models and provides approximately calibrated prediction intervals. Unlike existing methods, BCI is able to leverage multi-step ahead forecasts and explicitly optimize the average interval lengths by solving a one-dimensional stochastic control problem (SCP) at each time step. In particular, we use the dynamic programming algorithm to find the optimal policy for the SCP. We prove that BCI achieves long-term coverage under arbitrary distribution shifts and temporal dependence, even with poor multi-step ahead forecasts. We find empirically that BCI avoids uninformative intervals that have infinite lengths and generates substantially shorter prediction intervals in multiple applications when compared with existing methods.

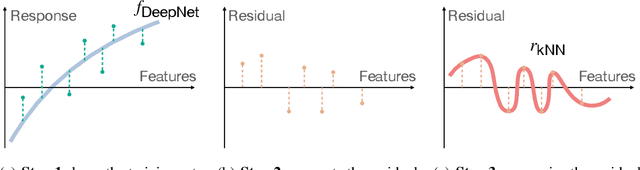
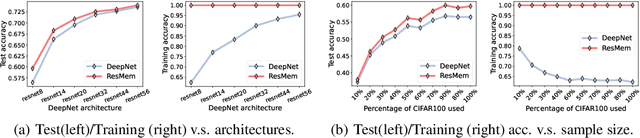
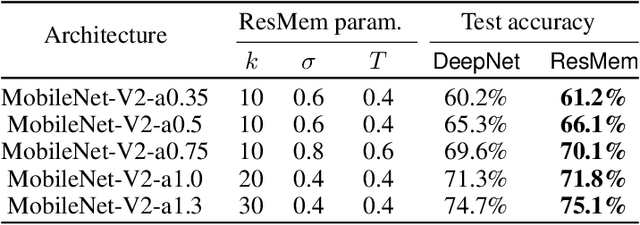
ResMem: Learn what you can and memorize the rest

The impressive generalization performance of modern neural networks is attributed in part to their ability to implicitly memorize complex training patterns. Inspired by this, we explore a novel mechanism to improve model generalization via explicit memorization. Specifically, we propose the residual-memorization (ResMem) algorithm, a new method that augments an existing prediction model (e.g. a neural network) by fitting the model's residuals with a $k$-nearest neighbor based regressor. The final prediction is then the sum of the original model and the fitted residual regressor. By construction, ResMem can explicitly memorize the training labels. Empirically, we show that ResMem consistently improves the test set generalization of the original prediction model across various standard vision and natural language processing benchmarks. Theoretically, we formulate a stylized linear regression problem and rigorously show that ResMem results in a more favorable test risk over the base predictor.

Predicting Out-of-Distribution Error with the Projection Norm

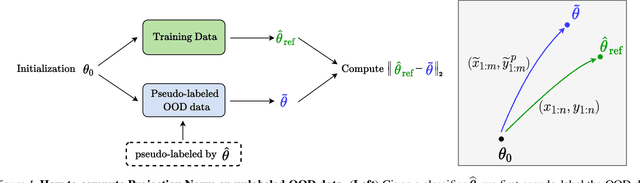
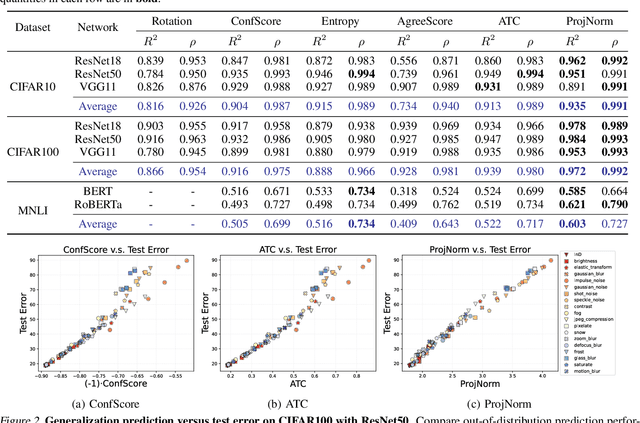
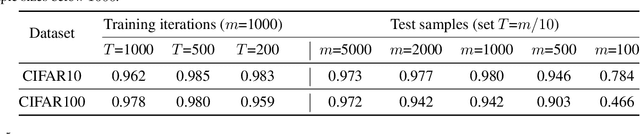
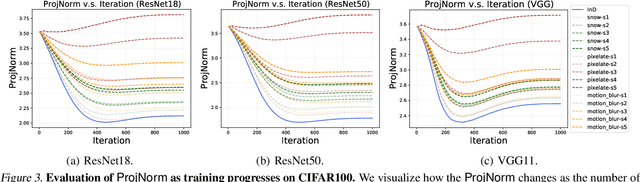
We propose a metric -- Projection Norm -- to predict a model's performance on out-of-distribution (OOD) data without access to ground truth labels. Projection Norm first uses model predictions to pseudo-label test samples and then trains a new model on the pseudo-labels. The more the new model's parameters differ from an in-distribution model, the greater the predicted OOD error. Empirically, our approach outperforms existing methods on both image and text classification tasks and across different network architectures. Theoretically, we connect our approach to a bound on the test error for overparameterized linear models. Furthermore, we find that Projection Norm is the only approach that achieves non-trivial detection performance on adversarial examples. Our code is available at https://github.com/yaodongyu/ProjNorm.

Understanding Generalization in Adversarial Training via the Bias-Variance Decomposition

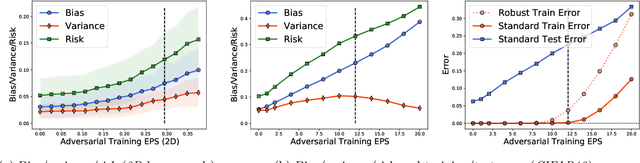
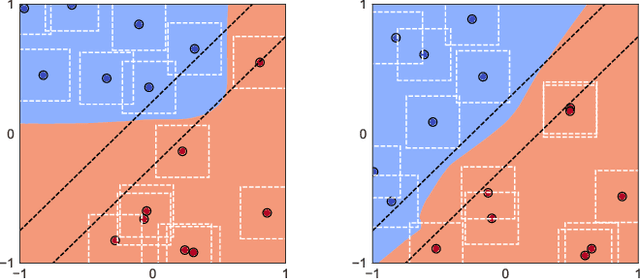
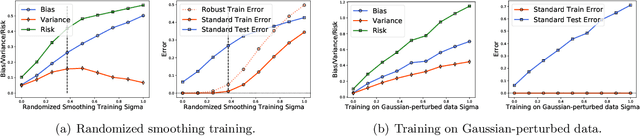
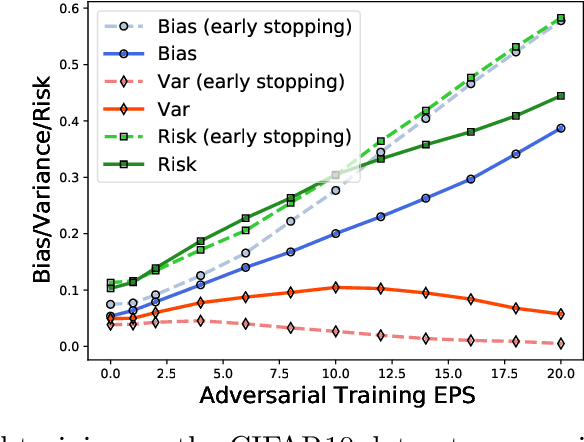
Adversarially trained models exhibit a large generalization gap: they can interpolate the training set even for large perturbation radii, but at the cost of large test error on clean samples. To investigate this gap, we decompose the test risk into its bias and variance components. We find that the bias increases monotonically with perturbation size and is the dominant term in the risk. Meanwhile, the variance is unimodal, peaking near the interpolation threshold for the training set. In contrast, we show that popular explanations for the generalization gap instead predict the variance to be monotonic, which leaves an unresolved mystery. We show that the same unimodal variance appears in a simple high-dimensional logistic regression problem, as well as for randomized smoothing. Overall, our results highlight the power of bias-variance decompositions in modern settings--by providing two measurements instead of one, they can rule out some theories and clarify others.

Exact Gap between Generalization Error and Uniform Convergence in Random Feature Models

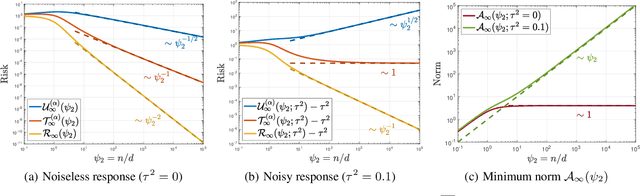
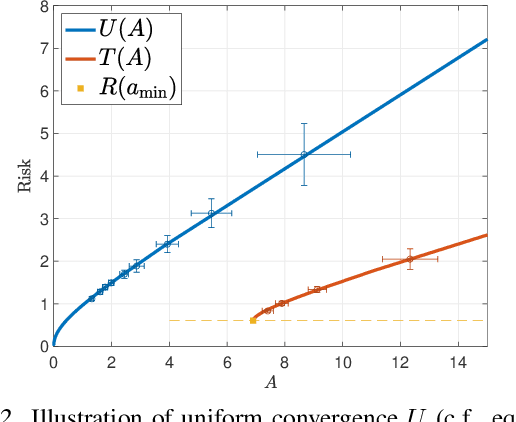
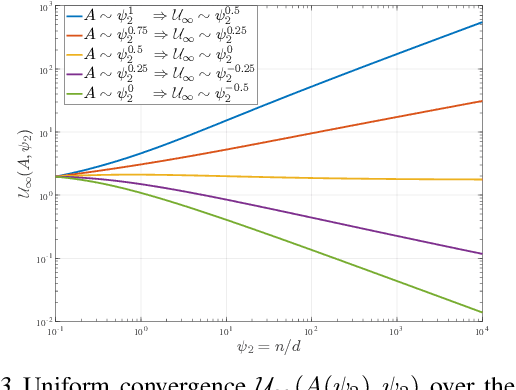
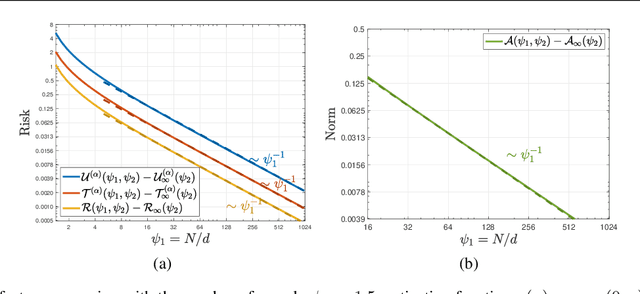
Recent work showed that there could be a large gap between the classical uniform convergence bound and the actual test error of zero-training-error predictors (interpolators) such as deep neural networks. To better understand this gap, we study the uniform convergence in the nonlinear random feature model and perform a precise theoretical analysis on how uniform convergence depends on the sample size and the number of parameters. We derive and prove analytical expressions for three quantities in this model: 1) classical uniform convergence over norm balls, 2) uniform convergence over interpolators in the norm ball (recently proposed by Zhou et al. (2020)), and 3) the risk of minimum norm interpolator. We show that, in the setting where the classical uniform convergence bound is vacuous (diverges to $\infty$), uniform convergence over the interpolators still gives a non-trivial bound of the test error of interpolating solutions. We also showcase a different setting where classical uniform convergence bound is non-vacuous, but uniform convergence over interpolators can give an improved sample complexity guarantee. Our result provides a first exact comparison between the test errors and uniform convergence bounds for interpolators beyond simple linear models.

Rethinking Bias-Variance Trade-off for Generalization of Neural Networks

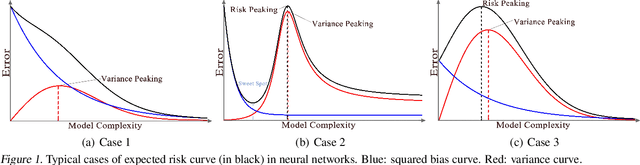
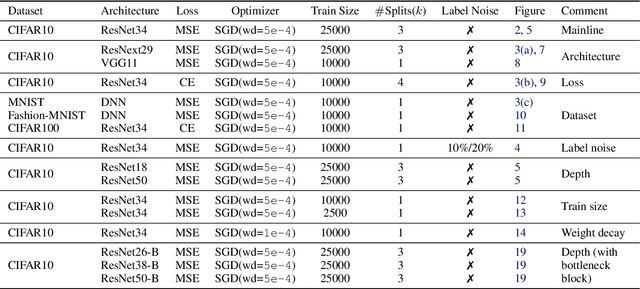
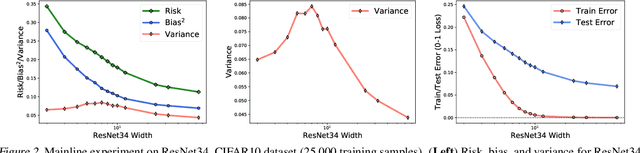
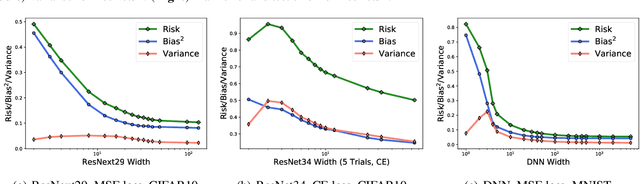
The classical bias-variance trade-off predicts that bias decreases and variance increase with model complexity, leading to a U-shaped risk curve. Recent work calls this into question for neural networks and other over-parameterized models, for which it is often observed that larger models generalize better. We provide a simple explanation for this by measuring the bias and variance of neural networks: while the bias is monotonically decreasing as in the classical theory, the variance is unimodal or bell-shaped: it increases then decreases with the width of the network. We vary the network architecture, loss function, and choice of dataset and confirm that variance unimodality occurs robustly for all models we considered. The risk curve is the sum of the bias and variance curves and displays different qualitative shapes depending on the relative scale of bias and variance, with the double descent curve observed in recent literature as a special case. We corroborate these empirical results with a theoretical analysis of two-layer linear networks with random first layer. Finally, evaluation on out-of-distribution data shows that most of the drop in accuracy comes from increased bias while variance increases by a relatively small amount. Moreover, we find that deeper models decrease bias and increase variance for both in-distribution and out-of-distribution data.

Complete Dictionary Learning via $\ell^4$-Norm Maximization over the Orthogonal Group

This paper considers the fundamental problem of learning a complete (orthogonal) dictionary from samples of sparsely generated signals. Most existing methods solve the dictionary (and sparse representations) based on heuristic algorithms, usually without theoretical guarantees for either optimality or complexity. The recent $\ell^1$-minimization based methods do provide such guarantees but the associated algorithms recover the dictionary one column at a time. In this work, we propose a new formulation that maximizes the $\ell^4$-norm over the orthogonal group, to learn the entire dictionary. We prove that under a random data model, with nearly minimum sample complexity, the global optima of the $\ell^4$ norm are very close to signed permutations of the ground truth. Inspired by this observation, we give a conceptually simple and yet effective algorithm based on "matching, stretching, and projection" (MSP). The algorithm provably converges locally at a superlinear (cubic) rate and cost per iteration is merely an SVD. In addition to strong theoretical guarantees, experiments show that the new algorithm is significantly more efficient and effective than existing methods, including KSVD and $\ell^1$-based methods. Preliminary experimental results on mixed real imagery data clearly demonstrate advantages of so learned dictionary over classic PCA bases.