Understanding Generalization in Adversarial Training via the Bias-Variance Decomposition

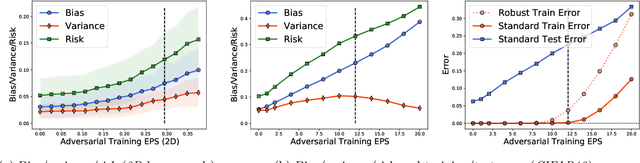
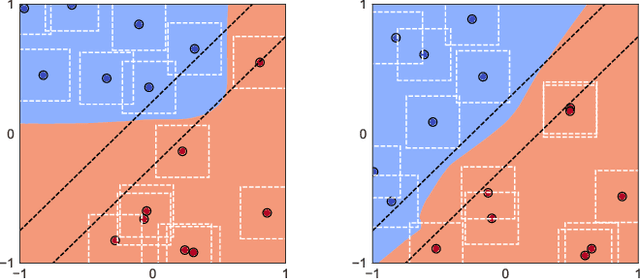
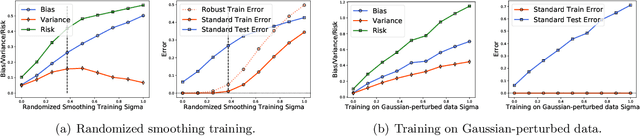
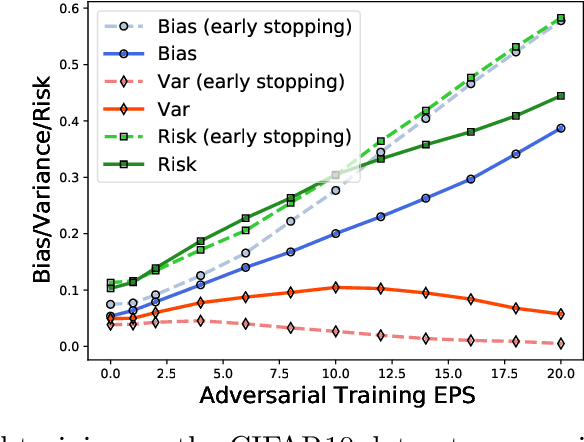
Adversarially trained models exhibit a large generalization gap: they can interpolate the training set even for large perturbation radii, but at the cost of large test error on clean samples. To investigate this gap, we decompose the test risk into its bias and variance components. We find that the bias increases monotonically with perturbation size and is the dominant term in the risk. Meanwhile, the variance is unimodal, peaking near the interpolation threshold for the training set. In contrast, we show that popular explanations for the generalization gap instead predict the variance to be monotonic, which leaves an unresolved mystery. We show that the same unimodal variance appears in a simple high-dimensional logistic regression problem, as well as for randomized smoothing. Overall, our results highlight the power of bias-variance decompositions in modern settings--by providing two measurements instead of one, they can rule out some theories and clarify others.