A Confidence Interval for the $\ell_2$ Expected Calibration Error

Recent advances in machine learning have significantly improved prediction accuracy in various applications. However, ensuring the calibration of probabilistic predictions remains a significant challenge. Despite efforts to enhance model calibration, the rigorous statistical evaluation of model calibration remains less explored. In this work, we develop confidence intervals the $\ell_2$ Expected Calibration Error (ECE). We consider top-1-to-$k$ calibration, which includes both the popular notion of confidence calibration as well as full calibration. For a debiased estimator of the ECE, we show asymptotic normality, but with different convergence rates and asymptotic variances for calibrated and miscalibrated models. We develop methods to construct asymptotically valid confidence intervals for the ECE, accounting for this behavior as well as non-negativity. Our theoretical findings are supported through extensive experiments, showing that our methods produce valid confidence intervals with shorter lengths compared to those obtained by resampling-based methods.

Watermarking Language Models with Error Correcting Codes

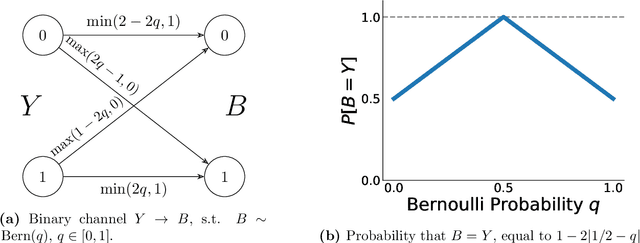
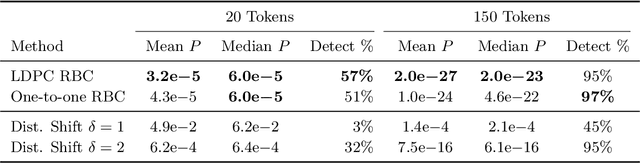
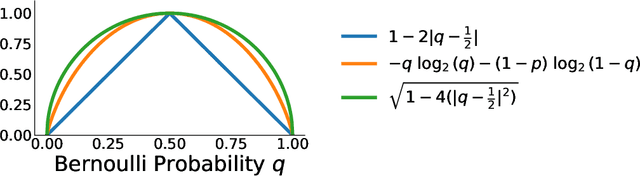
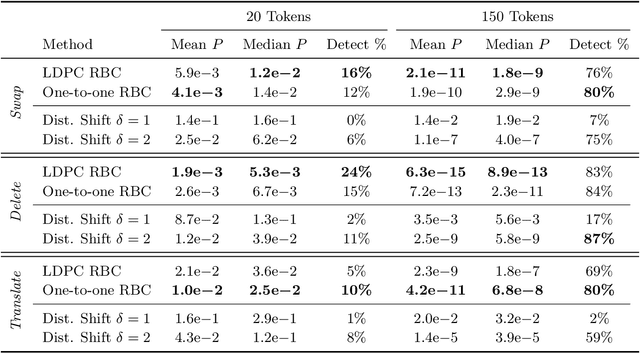
Recent progress in large language models enables the creation of realistic machine-generated content. Watermarking is a promising approach to distinguish machine-generated text from human text, embedding statistical signals in the output that are ideally undetectable to humans. We propose a watermarking framework that encodes such signals through an error correcting code. Our method, termed robust binary code (RBC) watermark, introduces no distortion compared to the original probability distribution, and no noticeable degradation in quality. We evaluate our watermark on base and instruction fine-tuned models and find our watermark is robust to edits, deletions, and translations. We provide an information-theoretic perspective on watermarking, a powerful statistical test for detection and for generating p-values, and theoretical guarantees. Our empirical findings suggest our watermark is fast, powerful, and robust, comparing favorably to the state-of-the-art.

One-Shot Safety Alignment for Large Language Models via Optimal Dualization

The growing safety concerns surrounding Large Language Models (LLMs) raise an urgent need to align them with diverse human preferences to simultaneously enhance their helpfulness and safety. A promising approach is to enforce safety constraints through Reinforcement Learning from Human Feedback (RLHF). For such constrained RLHF, common Lagrangian-based primal-dual policy optimization methods are computationally expensive and often unstable. This paper presents a dualization perspective that reduces constrained alignment to an equivalent unconstrained alignment problem. We do so by pre-optimizing a smooth and convex dual function that has a closed form. This shortcut eliminates the need for cumbersome primal-dual policy iterations, thus greatly reducing the computational burden and improving training stability. Our strategy leads to two practical algorithms in model-based and preference-based scenarios (MoCAN and PeCAN, respectively). A broad range of experiments demonstrate the effectiveness of our methods.

Uncertainty in Language Models: Assessment through Rank-Calibration

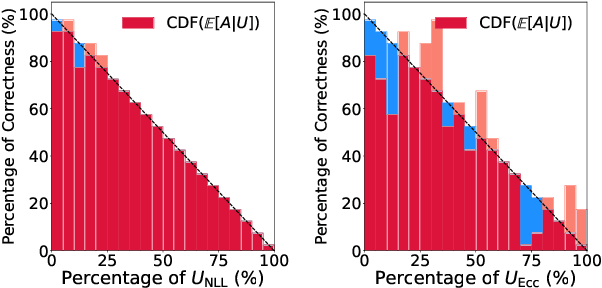
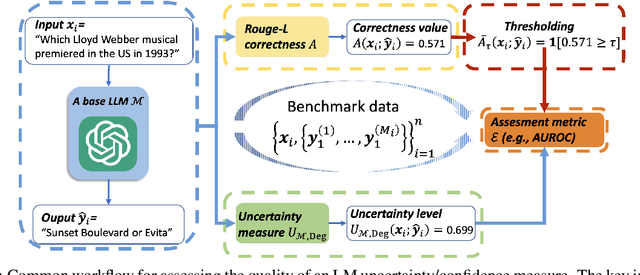
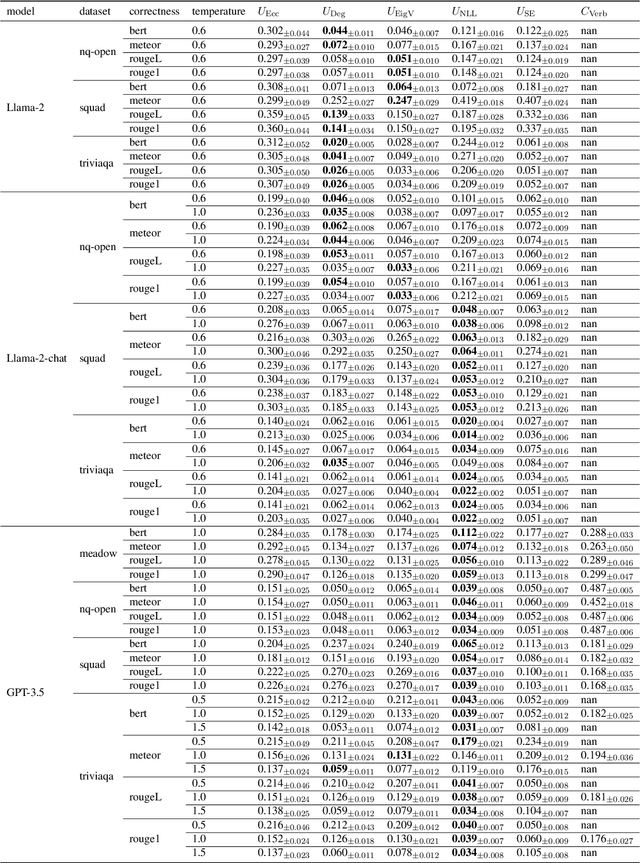
Language Models (LMs) have shown promising performance in natural language generation. However, as LMs often generate incorrect or hallucinated responses, it is crucial to correctly quantify their uncertainty in responding to given inputs. In addition to verbalized confidence elicited via prompting, many uncertainty measures ($e.g.$, semantic entropy and affinity-graph-based measures) have been proposed. However, these measures can differ greatly, and it is unclear how to compare them, partly because they take values over different ranges ($e.g.$, $[0,\infty)$ or $[0,1]$). In this work, we address this issue by developing a novel and practical framework, termed $Rank$-$Calibration$, to assess uncertainty and confidence measures for LMs. Our key tenet is that higher uncertainty (or lower confidence) should imply lower generation quality, on average. Rank-calibration quantifies deviations from this ideal relationship in a principled manner, without requiring ad hoc binary thresholding of the correctness score ($e.g.$, ROUGE or METEOR). The broad applicability and the granular interpretability of our methods are demonstrated empirically.

Inference in Randomized Least Squares and PCA via Normality of Quadratic Forms

Randomized algorithms can be used to speed up the analysis of large datasets. In this paper, we develop a unified methodology for statistical inference via randomized sketching or projections in two of the most fundamental problems in multivariate statistical analysis: least squares and PCA. The methodology applies to fixed datasets -- i.e., is data-conditional -- and the only randomness is due to the randomized algorithm. We propose statistical inference methods for a broad range of sketching distributions, such as the subsampled randomized Hadamard transform (SRHT), Sparse Sign Embeddings (SSE) and CountSketch, sketching matrices with i.i.d. entries, and uniform subsampling. To our knowledge, no comparable methods are available for SSE and for SRHT in PCA. Our novel theoretical approach rests on showing the asymptotic normality of certain quadratic forms. As a contribution of broader interest, we show central limit theorems for quadratic forms of the SRHT, relying on a novel proof via a dyadic expansion that leverages the recursive structure of the Hadamard transform. Numerical experiments using both synthetic and empirical datasets support the efficacy of our methods, and in particular suggest that sketching methods can have better computation-estimation tradeoffs than recently proposed optimal subsampling methods.

JailbreakBench: An Open Robustness Benchmark for Jailbreaking Large Language Models

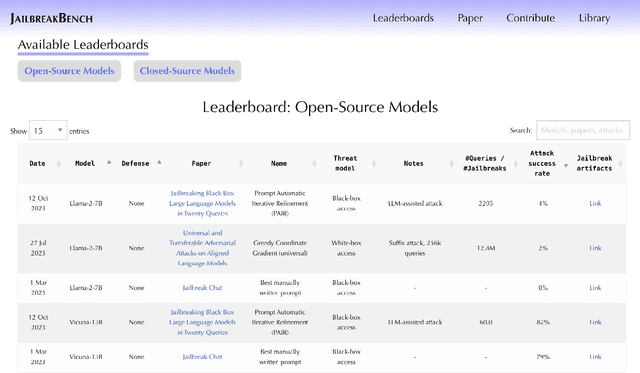
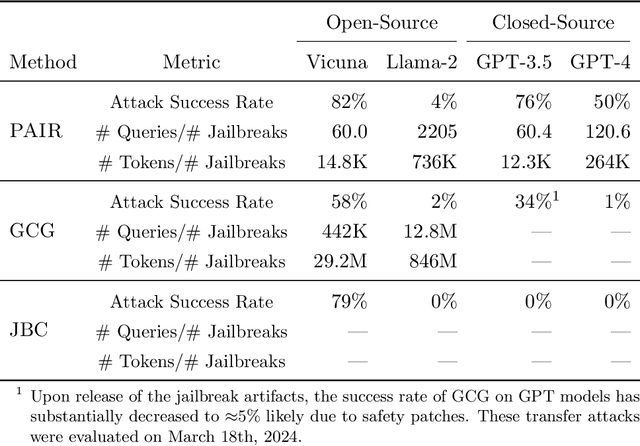
Jailbreak attacks cause large language models (LLMs) to generate harmful, unethical, or otherwise objectionable content. Evaluating these attacks presents a number of challenges, which the current collection of benchmarks and evaluation techniques do not adequately address. First, there is no clear standard of practice regarding jailbreaking evaluation. Second, existing works compute costs and success rates in incomparable ways. And third, numerous works are not reproducible, as they withhold adversarial prompts, involve closed-source code, or rely on evolving proprietary APIs. To address these challenges, we introduce JailbreakBench, an open-sourced benchmark with the following components: (1) a new jailbreaking dataset containing 100 unique behaviors, which we call JBB-Behaviors; (2) an evolving repository of state-of-the-art adversarial prompts, which we refer to as jailbreak artifacts; (3) a standardized evaluation framework that includes a clearly defined threat model, system prompts, chat templates, and scoring functions; and (4) a leaderboard that tracks the performance of attacks and defenses for various LLMs. We have carefully considered the potential ethical implications of releasing this benchmark, and believe that it will be a net positive for the community. Over time, we will expand and adapt the benchmark to reflect technical and methodological advances in the research community.

Minimax Optimal Fair Classification with Bounded Demographic Disparity

Mitigating the disparate impact of statistical machine learning methods is crucial for ensuring fairness. While extensive research aims to reduce disparity, the effect of using a \emph{finite dataset} -- as opposed to the entire population -- remains unclear. This paper explores the statistical foundations of fair binary classification with two protected groups, focusing on controlling demographic disparity, defined as the difference in acceptance rates between the groups. Although fairness may come at the cost of accuracy even with infinite data, we show that using a finite sample incurs additional costs due to the need to estimate group-specific acceptance thresholds. We study the minimax optimal classification error while constraining demographic disparity to a user-specified threshold. To quantify the impact of fairness constraints, we introduce a novel measure called \emph{fairness-aware excess risk} and derive a minimax lower bound on this measure that all classifiers must satisfy. Furthermore, we propose FairBayes-DDP+, a group-wise thresholding method with an offset that we show attains the minimax lower bound. Our lower bound proofs involve several innovations. Experiments support that FairBayes-DDP+ controls disparity at the user-specified level, while being faster and having a more favorable fairness-accuracy tradeoff than several baselines.

Bayes-Optimal Fair Classification with Linear Disparity Constraints via Pre-, In-, and Post-processing

Machine learning algorithms may have disparate impacts on protected groups. To address this, we develop methods for Bayes-optimal fair classification, aiming to minimize classification error subject to given group fairness constraints. We introduce the notion of \emph{linear disparity measures}, which are linear functions of a probabilistic classifier; and \emph{bilinear disparity measures}, which are also linear in the group-wise regression functions. We show that several popular disparity measures -- the deviations from demographic parity, equality of opportunity, and predictive equality -- are bilinear. We find the form of Bayes-optimal fair classifiers under a single linear disparity measure, by uncovering a connection with the Neyman-Pearson lemma. For bilinear disparity measures, Bayes-optimal fair classifiers become group-wise thresholding rules. Our approach can also handle multiple fairness constraints (such as equalized odds), and the common scenario when the protected attribute cannot be used at the prediction phase. Leveraging our theoretical results, we design methods that learn fair Bayes-optimal classifiers under bilinear disparity constraints. Our methods cover three popular approaches to fairness-aware classification, via pre-processing (Fair Up- and Down-Sampling), in-processing (Fair Cost-Sensitive Classification) and post-processing (a Fair Plug-In Rule). Our methods control disparity directly while achieving near-optimal fairness-accuracy tradeoffs. We show empirically that our methods compare favorably to existing algorithms.

SymmPI: Predictive Inference for Data with Group Symmetries

Quantifying the uncertainty of predictions is a core problem in modern statistics. Methods for predictive inference have been developed under a variety of assumptions, often -- for instance, in standard conformal prediction -- relying on the invariance of the distribution of the data under special groups of transformations such as permutation groups. Moreover, many existing methods for predictive inference aim to predict unobserved outcomes in sequences of feature-outcome observations. Meanwhile, there is interest in predictive inference under more general observation models (e.g., for partially observed features) and for data satisfying more general distributional symmetries (e.g., rotationally invariant or coordinate-independent observations in physics). Here we propose SymmPI, a methodology for predictive inference when data distributions have general group symmetries in arbitrary observation models. Our methods leverage the novel notion of distributional equivariant transformations, which process the data while preserving their distributional invariances. We show that SymmPI has valid coverage under distributional invariance and characterize its performance under distribution shift, recovering recent results as special cases. We apply SymmPI to predict unobserved values associated to vertices in a network, where the distribution is unchanged under relabelings that keep the network structure unchanged. In several simulations in a two-layer hierarchical model, and in an empirical data analysis example, SymmPI performs favorably compared to existing methods.

PAC Prediction Sets Under Label Shift

Prediction sets capture uncertainty by predicting sets of labels rather than individual labels, enabling downstream decisions to conservatively account for all plausible outcomes. Conformal inference algorithms construct prediction sets guaranteed to contain the true label with high probability. These guarantees fail to hold in the face of distribution shift, which is precisely when reliable uncertainty quantification can be most useful. We propose a novel algorithm for constructing prediction sets with PAC guarantees in the label shift setting. This method estimates the predicted probabilities of the classes in a target domain, as well as the confusion matrix, then propagates uncertainty in these estimates through a Gaussian elimination algorithm to compute confidence intervals for importance weights. Finally, it uses these intervals to construct prediction sets. We evaluate our approach on five datasets: the CIFAR-10, ChestX-Ray and Entity-13 image datasets, the tabular CDC Heart dataset, and the AGNews text dataset. Our algorithm satisfies the PAC guarantee while producing smaller, more informative, prediction sets compared to several baselines.