Minimax Optimal Fair Classification with Bounded Demographic Disparity

Mitigating the disparate impact of statistical machine learning methods is crucial for ensuring fairness. While extensive research aims to reduce disparity, the effect of using a \emph{finite dataset} -- as opposed to the entire population -- remains unclear. This paper explores the statistical foundations of fair binary classification with two protected groups, focusing on controlling demographic disparity, defined as the difference in acceptance rates between the groups. Although fairness may come at the cost of accuracy even with infinite data, we show that using a finite sample incurs additional costs due to the need to estimate group-specific acceptance thresholds. We study the minimax optimal classification error while constraining demographic disparity to a user-specified threshold. To quantify the impact of fairness constraints, we introduce a novel measure called \emph{fairness-aware excess risk} and derive a minimax lower bound on this measure that all classifiers must satisfy. Furthermore, we propose FairBayes-DDP+, a group-wise thresholding method with an offset that we show attains the minimax lower bound. Our lower bound proofs involve several innovations. Experiments support that FairBayes-DDP+ controls disparity at the user-specified level, while being faster and having a more favorable fairness-accuracy tradeoff than several baselines.

FairRR: Pre-Processing for Group Fairness through Randomized Response

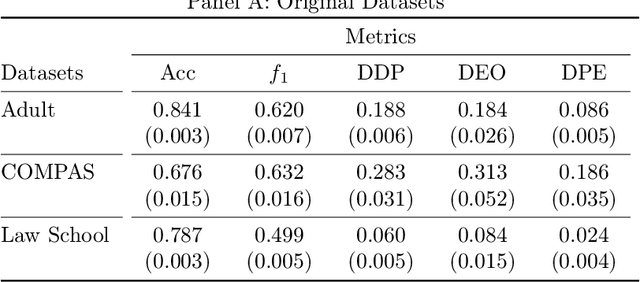
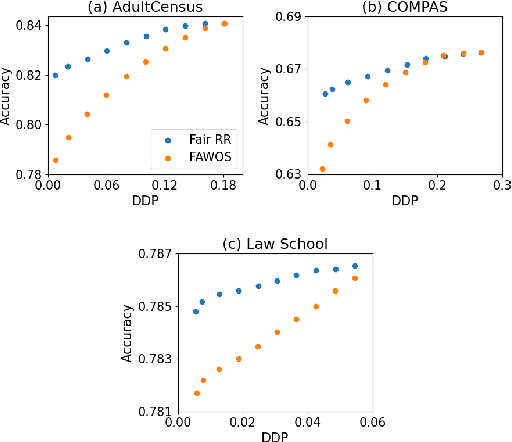
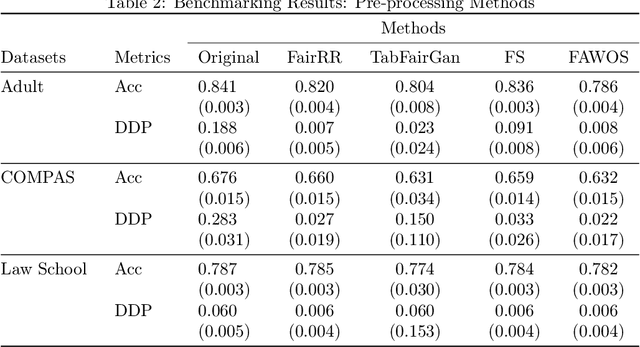
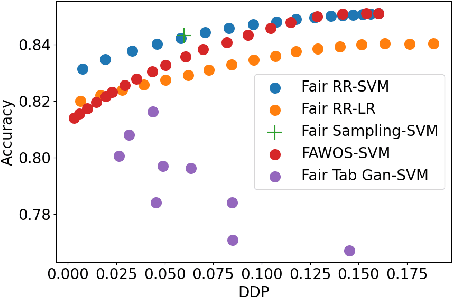
The increasing usage of machine learning models in consequential decision-making processes has spurred research into the fairness of these systems. While significant work has been done to study group fairness in the in-processing and post-processing setting, there has been little that theoretically connects these results to the pre-processing domain. This paper proposes that achieving group fairness in downstream models can be formulated as finding the optimal design matrix in which to modify a response variable in a Randomized Response framework. We show that measures of group fairness can be directly controlled for with optimal model utility, proposing a pre-processing algorithm called FairRR that yields excellent downstream model utility and fairness.

Bayes-Optimal Fair Classification with Linear Disparity Constraints via Pre-, In-, and Post-processing

Machine learning algorithms may have disparate impacts on protected groups. To address this, we develop methods for Bayes-optimal fair classification, aiming to minimize classification error subject to given group fairness constraints. We introduce the notion of \emph{linear disparity measures}, which are linear functions of a probabilistic classifier; and \emph{bilinear disparity measures}, which are also linear in the group-wise regression functions. We show that several popular disparity measures -- the deviations from demographic parity, equality of opportunity, and predictive equality -- are bilinear. We find the form of Bayes-optimal fair classifiers under a single linear disparity measure, by uncovering a connection with the Neyman-Pearson lemma. For bilinear disparity measures, Bayes-optimal fair classifiers become group-wise thresholding rules. Our approach can also handle multiple fairness constraints (such as equalized odds), and the common scenario when the protected attribute cannot be used at the prediction phase. Leveraging our theoretical results, we design methods that learn fair Bayes-optimal classifiers under bilinear disparity constraints. Our methods cover three popular approaches to fairness-aware classification, via pre-processing (Fair Up- and Down-Sampling), in-processing (Fair Cost-Sensitive Classification) and post-processing (a Fair Plug-In Rule). Our methods control disparity directly while achieving near-optimal fairness-accuracy tradeoffs. We show empirically that our methods compare favorably to existing algorithms.

Fair Bayes-Optimal Classifiers Under Predictive Parity

Increasing concerns about disparate effects of AI have motivated a great deal of work on fair machine learning. Existing works mainly focus on independence- and separation-based measures (e.g., demographic parity, equality of opportunity, equalized odds), while sufficiency-based measures such as predictive parity are much less studied. This paper considers predictive parity, which requires equalizing the probability of success given a positive prediction among different protected groups. We prove that, if the overall performances of different groups vary only moderately, all fair Bayes-optimal classifiers under predictive parity are group-wise thresholding rules. Perhaps surprisingly, this may not hold if group performance levels vary widely; in this case we find that predictive parity among protected groups may lead to within-group unfairness. We then propose an algorithm we call FairBayes-DPP, aiming to ensure predictive parity when our condition is satisfied. FairBayes-DPP is an adaptive thresholding algorithm that aims to achieve predictive parity, while also seeking to maximize test accuracy. We provide supporting experiments conducted on synthetic and empirical data.

Bayes-Optimal Classifiers under Group Fairness

Machine learning algorithms are becoming integrated into more and more high-stakes decision-making processes, such as in social welfare issues. Due to the need of mitigating the potentially disparate impacts from algorithmic predictions, many approaches have been proposed in the emerging area of fair machine learning. However, the fundamental problem of characterizing Bayes-optimal classifiers under various group fairness constraints has only been investigated in some special cases. Based on the classical Neyman-Pearson argument (Neyman and Pearson, 1933; Shao, 2003) for optimal hypothesis testing, this paper provides a unified framework for deriving Bayes-optimal classifiers under group fairness. This enables us to propose a group-based thresholding method that can directly control disparity, and more importantly, achieve an optimal fairness-accuracy tradeoff. These advantages are supported by experiments.