A Confidence Interval for the $\ell_2$ Expected Calibration Error

Recent advances in machine learning have significantly improved prediction accuracy in various applications. However, ensuring the calibration of probabilistic predictions remains a significant challenge. Despite efforts to enhance model calibration, the rigorous statistical evaluation of model calibration remains less explored. In this work, we develop confidence intervals the $\ell_2$ Expected Calibration Error (ECE). We consider top-1-to-$k$ calibration, which includes both the popular notion of confidence calibration as well as full calibration. For a debiased estimator of the ECE, we show asymptotic normality, but with different convergence rates and asymptotic variances for calibrated and miscalibrated models. We develop methods to construct asymptotically valid confidence intervals for the ECE, accounting for this behavior as well as non-negativity. Our theoretical findings are supported through extensive experiments, showing that our methods produce valid confidence intervals with shorter lengths compared to those obtained by resampling-based methods.

Sparse Neural Additive Model: Interpretable Deep Learning with Feature Selection via Group Sparsity

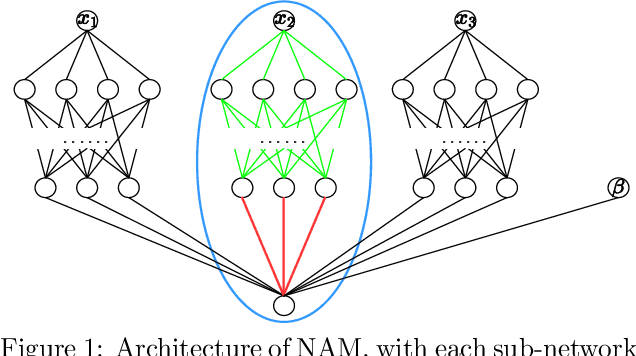
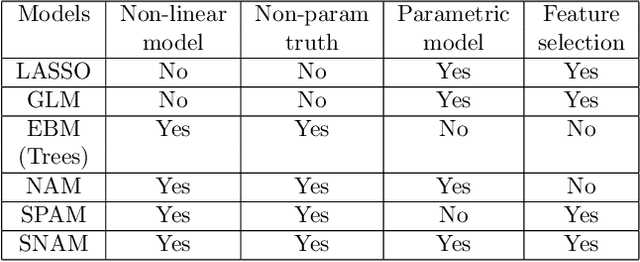
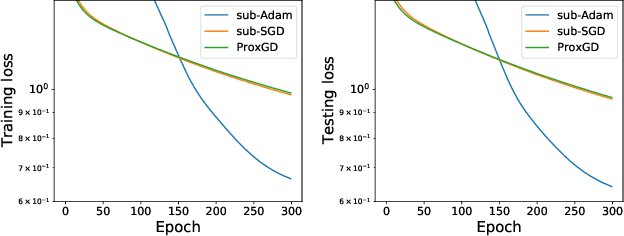
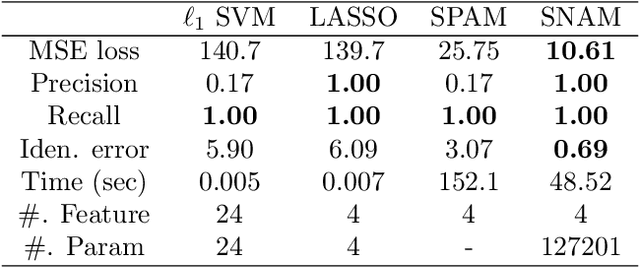
Interpretable machine learning has demonstrated impressive performance while preserving explainability. In particular, neural additive models (NAM) offer the interpretability to the black-box deep learning and achieve state-of-the-art accuracy among the large family of generalized additive models. In order to empower NAM with feature selection and improve the generalization, we propose the sparse neural additive models (SNAM) that employ the group sparsity regularization (e.g. Group LASSO), where each feature is learned by a sub-network whose trainable parameters are clustered as a group. We study the theoretical properties for SNAM with novel techniques to tackle the non-parametric truth, thus extending from classical sparse linear models such as the LASSO, which only works on the parametric truth. Specifically, we show that SNAM with subgradient and proximal gradient descents provably converges to zero training loss as $t\to\infty$, and that the estimation error of SNAM vanishes asymptotically as $n\to\infty$. We also prove that SNAM, similar to LASSO, can have exact support recovery, i.e. perfect feature selection, with appropriate regularization. Moreover, we show that the SNAM can generalize well and preserve the `identifiability', recovering each feature's effect. We validate our theories via extensive experiments and further testify to the good accuracy and efficiency of SNAM.