Automatic gradient descent with generalized Newton's method

We propose the generalized Newton's method (GeN) -- a Hessian-informed approach that applies to any optimizer such as SGD and Adam, and covers the Newton-Raphson method as a sub-case. Our method automatically and dynamically selects the learning rate that accelerates the convergence, without the intensive tuning of the learning rate scheduler. In practice, out method is easily implementable, since it only requires additional forward passes with almost zero computational overhead (in terms of training time and memory cost), if the overhead is amortized over many iterations. We present extensive experiments on language and vision tasks (e.g. GPT and ResNet) to showcase that GeN optimizers match the state-of-the-art performance, which was achieved with carefully tuned learning rate schedulers. Code to be released at \url{https://github.com/ShiyunXu/AutoGeN}.

Scalable and Efficient Training of Large Convolutional Neural Networks with Differential Privacy

Large convolutional neural networks (CNN) can be difficult to train in the differentially private (DP) regime, since the optimization algorithms require a computationally expensive operation, known as the per-sample gradient clipping. We propose an efficient and scalable implementation of this clipping on convolutional layers, termed as the mixed ghost clipping, that significantly eases the private training in terms of both time and space complexities, without affecting the accuracy. The improvement in efficiency is rigorously studied through the first complexity analysis for the mixed ghost clipping and existing DP training algorithms. Extensive experiments on vision classification tasks, with large ResNet, VGG, and Vision Transformers, demonstrate that DP training with mixed ghost clipping adds $1\sim 10\%$ memory overhead and $<2\times$ slowdown to the standard non-private training. Specifically, when training VGG19 on CIFAR10, the mixed ghost clipping is $3\times$ faster than state-of-the-art Opacus library with $18\times$ larger maximum batch size. To emphasize the significance of efficient DP training on convolutional layers, we achieve 96.7\% accuracy on CIFAR10 and 83.0\% on CIFAR100 at $\epsilon=1$ using BEiT, while the previous best results are 94.8\% and 67.4\%, respectively. We open-source a privacy engine (\url{https://github.com/JialinMao/private_CNN}) that implements DP training of CNN with a few lines of code.

Sparse Neural Additive Model: Interpretable Deep Learning with Feature Selection via Group Sparsity

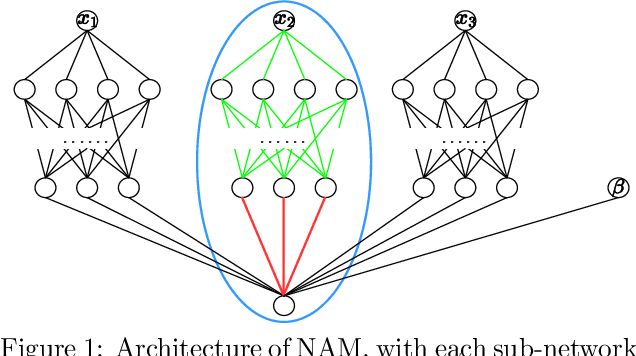
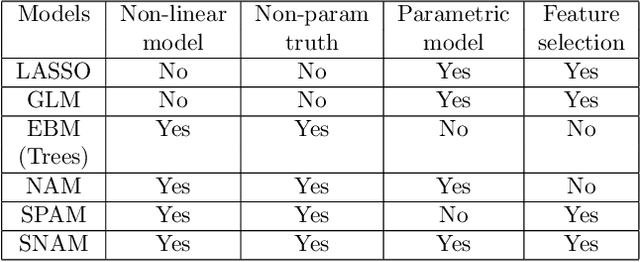
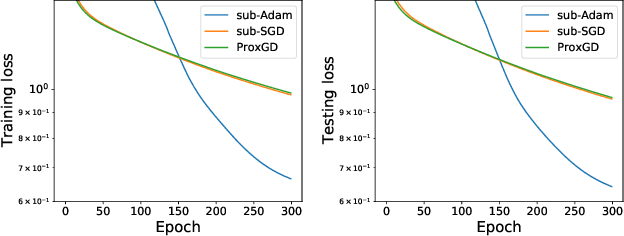
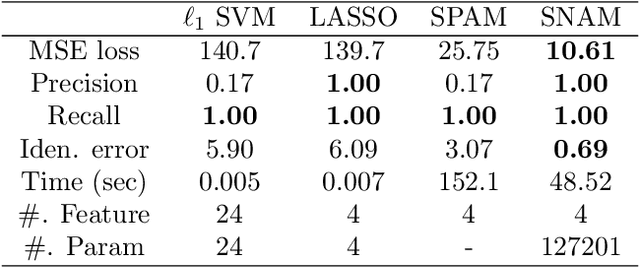
Interpretable machine learning has demonstrated impressive performance while preserving explainability. In particular, neural additive models (NAM) offer the interpretability to the black-box deep learning and achieve state-of-the-art accuracy among the large family of generalized additive models. In order to empower NAM with feature selection and improve the generalization, we propose the sparse neural additive models (SNAM) that employ the group sparsity regularization (e.g. Group LASSO), where each feature is learned by a sub-network whose trainable parameters are clustered as a group. We study the theoretical properties for SNAM with novel techniques to tackle the non-parametric truth, thus extending from classical sparse linear models such as the LASSO, which only works on the parametric truth. Specifically, we show that SNAM with subgradient and proximal gradient descents provably converges to zero training loss as $t\to\infty$, and that the estimation error of SNAM vanishes asymptotically as $n\to\infty$. We also prove that SNAM, similar to LASSO, can have exact support recovery, i.e. perfect feature selection, with appropriate regularization. Moreover, we show that the SNAM can generalize well and preserve the `identifiability', recovering each feature's effect. We validate our theories via extensive experiments and further testify to the good accuracy and efficiency of SNAM.

DebiNet: Debiasing Linear Models with Nonlinear Overparameterized Neural Networks

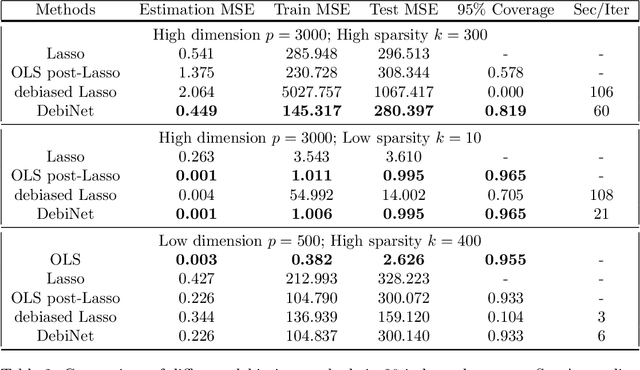
Recent years have witnessed strong empirical performance of over-parameterized neural networks on various tasks and many advances in the theory, e.g. the universal approximation and provable convergence to global minimum. In this paper, we incorporate over-parameterized neural networks into semi-parametric models to bridge the gap between inference and prediction, especially in the high dimensional linear problem. By doing so, we can exploit a wide class of networks to approximate the nuisance functions and to estimate the parameters of interest consistently. Therefore, we may offer the best of two worlds: the universal approximation ability from neural networks and the interpretability from classic ordinary linear model, leading to valid inference and accurate prediction. We show the theoretical foundations that make this possible and demonstrate with numerical experiments. Furthermore, we propose a framework, DebiNet, in which we plug-in arbitrary feature selection methods to our semi-parametric neural network and illustrate that our framework debiases the regularized estimators and performs well, in terms of the post-selection inference and the generalization error.

A Dynamical View on Optimization Algorithms of Overparameterized Neural Networks

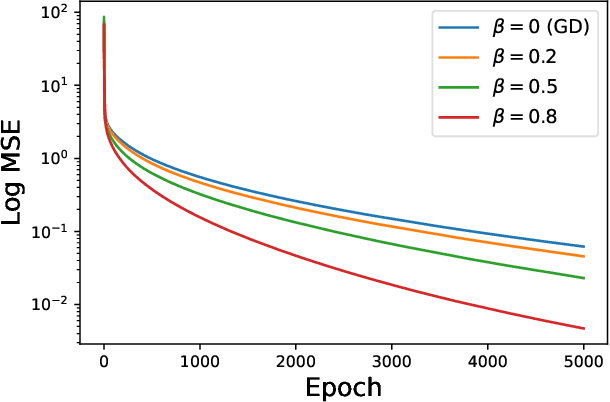
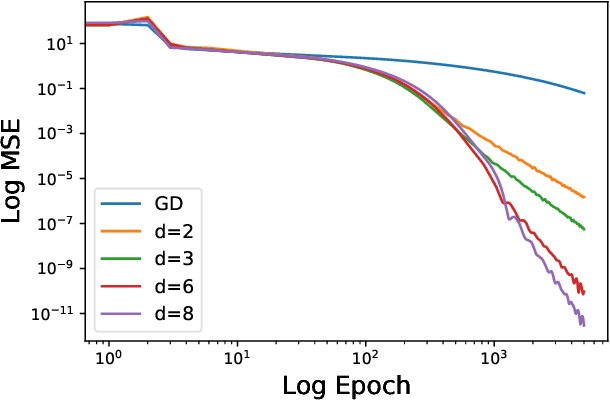
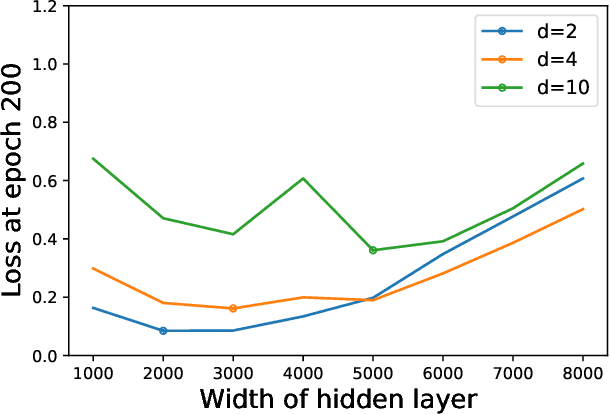
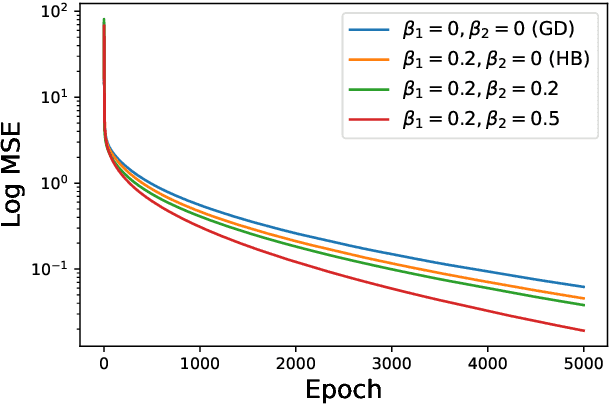
When equipped with efficient optimization algorithms, the over-parameterized neural networks have demonstrated high level of performance even though the loss function is non-convex and non-smooth. While many works have been focusing on understanding the loss dynamics by training neural networks with the gradient descent (GD), in this work, we consider a broad class of optimization algorithms that are commonly used in practice. For example, we show from a dynamical system perspective that the Heavy Ball (HB) method can converge to global minimum on mean squared error (MSE) at a linear rate (similar to GD); however, the Nesterov accelerated gradient descent (NAG) only converges to global minimum sublinearly. Our results rely on the connection between neural tangent kernel (NTK) and finite over-parameterized neural networks with ReLU activation, which leads to analyzing the limiting ordinary differential equations (ODE) for optimization algorithms. We show that, optimizing the non-convex loss over the weights corresponds to optimizing some strongly convex loss over the prediction error. As a consequence, we can leverage the classical convex optimization theory to understand the convergence behavior of neural networks. We believe our approach can also be extended to other loss functions and network architectures.