A Hessian-informed hyperparameter optimization for differential learning rate

Differential learning rate (DLR), a technique that applies different learning rates to different model parameters, has been widely used in deep learning and achieved empirical success via its various forms. For example, parameter-efficient fine-tuning (PEFT) applies zero learning rates to most parameters so as to significantly save the computational cost. At the core, DLR leverages the observation that different parameters can have different loss curvature, which is hard to characterize in general. We propose the Hessian-informed differential learning rate (Hi-DLR), an efficient approach that solves the hyperparameter optimization (HPO) of learning rates and captures the loss curvature for any model and optimizer adaptively. Given a proper grouping of parameters, we empirically demonstrate that Hi-DLR can improve the convergence by dynamically determining the learning rates during the training. Furthermore, we can quantify the influence of different parameters and freeze the less-contributing parameters, which leads to a new PEFT that automatically adapts to various tasks and models. Additionally, Hi-DLR also exhibits comparable performance on various full model training tasks.

Federated Learning with Extremely Noisy Clients via Negative Distillation

Federated learning (FL) has shown remarkable success in cooperatively training deep models, while typically struggling with noisy labels. Advanced works propose to tackle label noise by a re-weighting strategy with a strong assumption, i.e., mild label noise. However, it may be violated in many real-world FL scenarios because of highly contaminated clients, resulting in extreme noise ratios, e.g., $>$90%. To tackle extremely noisy clients, we study the robustness of the re-weighting strategy, showing a pessimistic conclusion: minimizing the weight of clients trained over noisy data outperforms re-weighting strategies. To leverage models trained on noisy clients, we propose a novel approach, called negative distillation (FedNed). FedNed first identifies noisy clients and employs rather than discards the noisy clients in a knowledge distillation manner. In particular, clients identified as noisy ones are required to train models using noisy labels and pseudo-labels obtained by global models. The model trained on noisy labels serves as a `bad teacher' in knowledge distillation, aiming to decrease the risk of providing incorrect information. Meanwhile, the model trained on pseudo-labels is involved in model aggregation if not identified as a noisy client. Consequently, through pseudo-labeling, FedNed gradually increases the trustworthiness of models trained on noisy clients, while leveraging all clients for model aggregation through negative distillation. To verify the efficacy of FedNed, we conduct extensive experiments under various settings, demonstrating that FedNed can consistently outperform baselines and achieve state-of-the-art performance. Our code is available at https://github.com/linChen99/FedNed.

MISNN: Multiple Imputation via Semi-parametric Neural Networks

Multiple imputation (MI) has been widely applied to missing value problems in biomedical, social and econometric research, in order to avoid improper inference in the downstream data analysis. In the presence of high-dimensional data, imputation models that include feature selection, especially $\ell_1$ regularized regression (such as Lasso, adaptive Lasso, and Elastic Net), are common choices to prevent the model from underdetermination. However, conducting MI with feature selection is difficult: existing methods are often computationally inefficient and poor in performance. We propose MISNN, a novel and efficient algorithm that incorporates feature selection for MI. Leveraging the approximation power of neural networks, MISNN is a general and flexible framework, compatible with any feature selection method, any neural network architecture, high/low-dimensional data and general missing patterns. Through empirical experiments, MISNN has demonstrated great advantages over state-of-the-art imputation methods (e.g. Bayesian Lasso and matrix completion), in terms of imputation accuracy, statistical consistency and computation speed.

Combating Noisy-Labeled and Imbalanced Data by Two Stage Bi-Dimensional Sample Selection

Robust learning on noisy-labeled data has been an important task in real applications, because label noise directly leads to the poor generalization of deep learning models. Existing label-noise learning methods usually assume that the ground-truth classes of the training data are balanced. However, the real-world data is often imbalanced, leading to the inconsistency between observed and intrinsic class distribution due to label noises. Distribution inconsistency makes the problem of label-noise learning more challenging because it is hard to distinguish clean samples from noisy samples on the intrinsic tail classes. In this paper, we propose a learning framework for label-noise learning with intrinsically long-tailed data. Specifically, we propose a robust sample selection method called two-stage bi-dimensional sample selection (TBSS) to better separate clean samples from noisy samples, especially for the tail classes. TBSS consists of two new separation metrics to jointly separate samples in each class. Extensive experiments on multiple noisy-labeled datasets with intrinsically long-tailed class distribution demonstrate the effectiveness of our method.

Assessing Fairness in the Presence of Missing Data

Missing data are prevalent and present daunting challenges in real data analysis. While there is a growing body of literature on fairness in analysis of fully observed data, there has been little theoretical work on investigating fairness in analysis of incomplete data. In practice, a popular analytical approach for dealing with missing data is to use only the set of complete cases, i.e., observations with all features fully observed to train a prediction algorithm. However, depending on the missing data mechanism, the distribution of complete cases and the distribution of the complete data may be substantially different. When the goal is to develop a fair algorithm in the complete data domain where there are no missing values, an algorithm that is fair in the complete case domain may show disproportionate bias towards some marginalized groups in the complete data domain. To fill this significant gap, we study the problem of estimating fairness in the complete data domain for an arbitrary model evaluated merely using complete cases. We provide upper and lower bounds on the fairness estimation error and conduct numerical experiments to assess our theoretical results. Our work provides the first known theoretical results on fairness guarantee in analysis of incomplete data.

Fairness in Missing Data Imputation

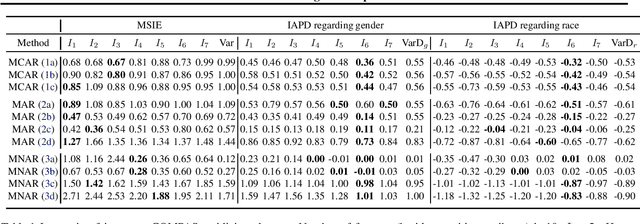
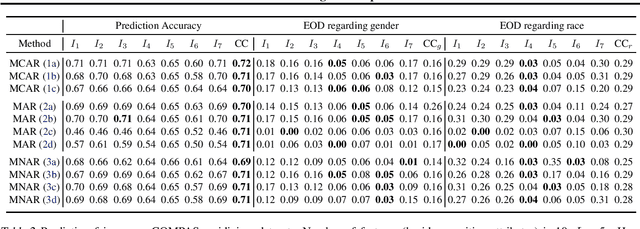
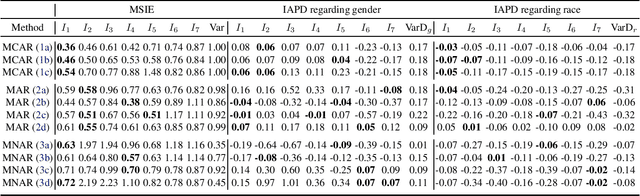
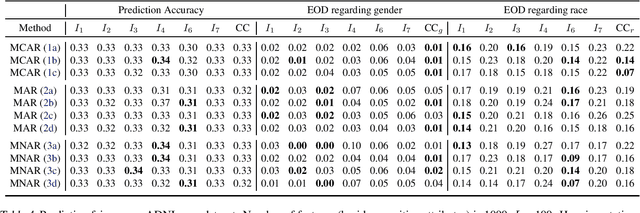
Missing data are ubiquitous in the era of big data and, if inadequately handled, are known to lead to biased findings and have deleterious impact on data-driven decision makings. To mitigate its impact, many missing value imputation methods have been developed. However, the fairness of these imputation methods across sensitive groups has not been studied. In this paper, we conduct the first known research on fairness of missing data imputation. By studying the performance of imputation methods in three commonly used datasets, we demonstrate that unfairness of missing value imputation widely exists and may be associated with multiple factors. Our results suggest that, in practice, a careful investigation of related factors can provide valuable insights on mitigating unfairness associated with missing data imputation.

An Unconstrained Layer-Peeled Perspective on Neural Collapse

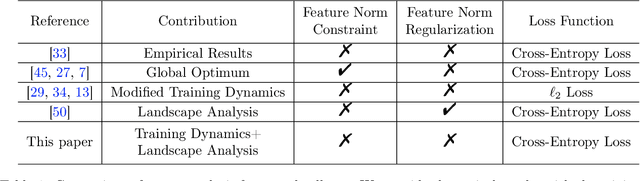
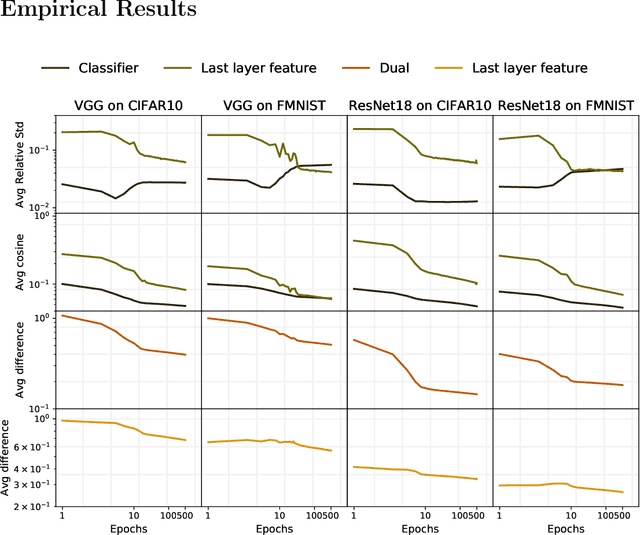
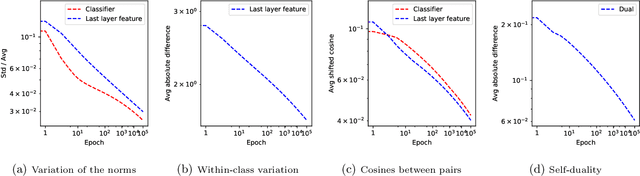
Neural collapse is a highly symmetric geometric pattern of neural networks that emerges during the terminal phase of training, with profound implications on the generalization performance and robustness of the trained networks. To understand how the last-layer features and classifiers exhibit this recently discovered implicit bias, in this paper, we introduce a surrogate model called the unconstrained layer-peeled model (ULPM). We prove that gradient flow on this model converges to critical points of a minimum-norm separation problem exhibiting neural collapse in its global minimizer. Moreover, we show that the ULPM with the cross-entropy loss has a benign global landscape for its loss function, which allows us to prove that all the critical points are strict saddle points except the global minimizers that exhibit the neural collapse phenomenon. Empirically, we show that our results also hold during the training of neural networks in real-world tasks when explicit regularization or weight decay is not used.

Efficient Designs of SLOPE Penalty Sequences in Finite Dimension

In linear regression, SLOPE is a new convex analysis method that generalizes the Lasso via the sorted L1 penalty: larger fitted coefficients are penalized more heavily. This magnitude-dependent regularization requires an input of penalty sequence $\lambda$, instead of a scalar penalty as in the Lasso case, thus making the design extremely expensive in computation. In this paper, we propose two efficient algorithms to design the possibly high-dimensional SLOPE penalty, in order to minimize the mean squared error. For Gaussian data matrices, we propose a first order Projected Gradient Descent (PGD) under the Approximate Message Passing regime. For general data matrices, we present a zero-th order Coordinate Descent (CD) to design a sub-class of SLOPE, referred to as the k-level SLOPE. Our CD allows a useful trade-off between the accuracy and the computation speed. We demonstrate the performance of SLOPE with our designs via extensive experiments on synthetic data and real-world datasets.

A general kernel boosting framework integrating pathways for predictive modeling based on genomic data

Predictive modeling based on genomic data has gained popularity in biomedical research and clinical practice by allowing researchers and clinicians to identify biomarkers and tailor treatment decisions more efficiently. Analysis incorporating pathway information can boost discovery power and better connect new findings with biological mechanisms. In this article, we propose a general framework, Pathway-based Kernel Boosting (PKB), which incorporates clinical information and prior knowledge about pathways for prediction of binary, continuous and survival outcomes. We introduce appropriate loss functions and optimization procedures for different outcome types. Our prediction algorithm incorporates pathway knowledge by constructing kernel function spaces from the pathways and use them as base learners in the boosting procedure. Through extensive simulations and case studies in drug response and cancer survival datasets, we demonstrate that PKB can substantially outperform other competing methods, better identify biological pathways related to drug response and patient survival, and provide novel insights into cancer pathogenesis and treatment response.