An Unconstrained Layer-Peeled Perspective on Neural Collapse
Paper and Code
Oct 06, 2021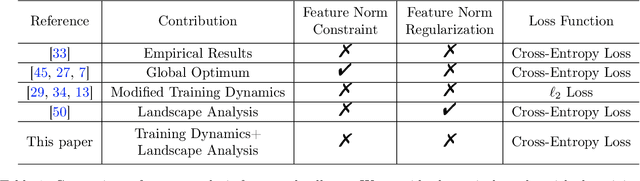
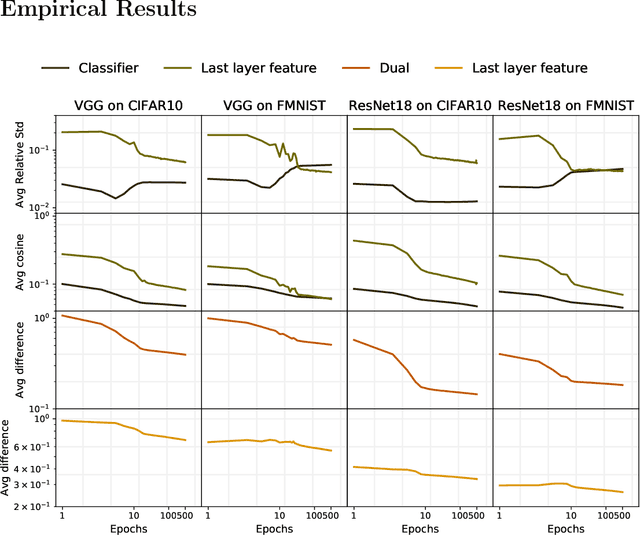
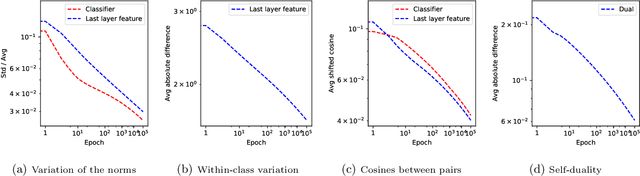
Neural collapse is a highly symmetric geometric pattern of neural networks that emerges during the terminal phase of training, with profound implications on the generalization performance and robustness of the trained networks. To understand how the last-layer features and classifiers exhibit this recently discovered implicit bias, in this paper, we introduce a surrogate model called the unconstrained layer-peeled model (ULPM). We prove that gradient flow on this model converges to critical points of a minimum-norm separation problem exhibiting neural collapse in its global minimizer. Moreover, we show that the ULPM with the cross-entropy loss has a benign global landscape for its loss function, which allows us to prove that all the critical points are strict saddle points except the global minimizers that exhibit the neural collapse phenomenon. Empirically, we show that our results also hold during the training of neural networks in real-world tasks when explicit regularization or weight decay is not used.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge