Multi-Round Human-AI Collaboration with User-Specified Requirements

As humans increasingly rely on multiround conversational AI for high stakes decisions, principled frameworks are needed to ensure such interactions reliably improve decision quality. We adopt a human centric view governed by two principles: counterfactual harm, ensuring the AI does not undermine human strengths, and complementarity, ensuring it adds value where the human is prone to err. We formalize these concepts via user defined rules, allowing users to specify exactly what harm and complementarity mean for their specific task. We then introduce an online, distribution free algorithm with finite sample guarantees that enforces the user-specified constraints over the collaboration dynamics. We evaluate our framework across two interactive settings: LLM simulated collaboration on a medical diagnostic task and a human crowdsourcing study on a pictorial reasoning task. We show that our online procedure maintains prescribed counterfactual harm and complementarity violation rates even under nonstationary interaction dynamics. Moreover, tightening or loosening these constraints produces predictable shifts in downstream human accuracy, confirming that the two principles serve as practical levers for steering multi-round collaboration toward better decision quality without the need to model or constrain human behavior.

When to Trust the Cheap Check: Weak and Strong Verification for Reasoning

Reasoning with LLMs increasingly unfolds inside a broader verification loop. Internally, systems use cheap checks, such as self-consistency or proxy rewards, which we call weak verification. Externally, users inspect outputs and steer the model through feedback until results are trustworthy, which we call strong verification. These signals differ sharply in cost and reliability: strong verification can establish trust but is resource-intensive, while weak verification is fast and scalable but noisy and imperfect. We formalize this tension through weak--strong verification policies, which decide when to accept or reject based on weak verification and when to defer to strong verification. We introduce metrics capturing incorrect acceptance, incorrect rejection, and strong-verification frequency. Over population, we show that optimal policies admit a two-threshold structure and that calibration and sharpness govern the value of weak verifiers. Building on this, we develop an online algorithm that provably controls acceptance and rejection errors without assumptions on the query stream, the language model, or the weak verifier.

Conformal Prediction Beyond the Seen: A Missing Mass Perspective for Uncertainty Quantification in Generative Models

Uncertainty quantification (UQ) is essential for safe deployment of generative AI models such as large language models (LLMs), especially in high stakes applications. Conformal prediction (CP) offers a principled uncertainty quantification framework, but classical methods focus on regression and classification, relying on geometric distances or softmax scores: tools that presuppose structured outputs. We depart from this paradigm by studying CP in a query only setting, where prediction sets must be constructed solely from finite queries to a black box generative model, introducing a new trade off between coverage, test time query budget, and informativeness. We introduce Conformal Prediction with Query Oracle (CPQ), a framework characterizing the optimal interplay between these objectives. Our finite sample algorithm is built on two core principles: one governs the optimal query policy, and the other defines the optimal mapping from queried samples to prediction sets. Remarkably, both are rooted in the classical missing mass problem in statistics. Specifically, the optimal query policy depends on the rate of decay, or the derivative, of the missing mass, for which we develop a novel estimator. Meanwhile, the optimal mapping hinges on the missing mass itself, which we estimate using Good Turing estimators. We then turn our focus to implementing our method for language models, where outputs are vast, variable, and often under specified. Fine grained experiments on three real world open ended tasks and two LLMs, show CPQ applicability to any black box LLM and highlight: (1) individual contribution of each principle to CPQ performance, and (2) CPQ ability to yield significantly more informative prediction sets than existing conformal methods for language uncertainty quantification.

Likelihood-Ratio Regularized Quantile Regression: Adapting Conformal Prediction to High-Dimensional Covariate Shifts

We consider the problem of conformal prediction under covariate shift. Given labeled data from a source domain and unlabeled data from a covariate shifted target domain, we seek to construct prediction sets with valid marginal coverage in the target domain. Most existing methods require estimating the unknown likelihood ratio function, which can be prohibitive for high-dimensional data such as images. To address this challenge, we introduce the likelihood ratio regularized quantile regression (LR-QR) algorithm, which combines the pinball loss with a novel choice of regularization in order to construct a threshold function without directly estimating the unknown likelihood ratio. We show that the LR-QR method has coverage at the desired level in the target domain, up to a small error term that we can control. Our proofs draw on a novel analysis of coverage via stability bounds from learning theory. Our experiments demonstrate that the LR-QR algorithm outperforms existing methods on high-dimensional prediction tasks, including a regression task for the Communities and Crime dataset, and an image classification task from the WILDS repository.

Decision Theoretic Foundations for Conformal Prediction: Optimal Uncertainty Quantification for Risk-Averse Agents

A fundamental question in data-driven decision making is how to quantify the uncertainty of predictions in ways that can usefully inform downstream action. This interface between prediction uncertainty and decision-making is especially important in risk-sensitive domains, such as medicine. In this paper, we develop decision-theoretic foundations that connect uncertainty quantification using prediction sets with risk-averse decision-making. Specifically, we answer three fundamental questions: (1) What is the correct notion of uncertainty quantification for risk-averse decision makers? We prove that prediction sets are optimal for decision makers who wish to optimize their value at risk. (2) What is the optimal policy that a risk averse decision maker should use to map prediction sets to actions? We show that a simple max-min decision policy is optimal for risk-averse decision makers. Finally, (3) How can we derive prediction sets that are optimal for such decision makers? We provide an exact characterization in the population regime and a distribution free finite-sample construction. Answering these questions naturally leads to an algorithm, Risk-Averse Calibration (RAC), which follows a provably optimal design for deriving action policies from predictions. RAC is designed to be both practical-capable of leveraging the quality of predictions in a black-box manner to enhance downstream utility-and safe-adhering to a user-defined risk threshold and optimizing the corresponding risk quantile of the user's downstream utility. Finally, we experimentally demonstrate the significant advantages of RAC in applications such as medical diagnosis and recommendation systems. Specifically, we show that RAC achieves a substantially improved trade-off between safety and utility, offering higher utility compared to existing methods while maintaining the safety guarantee.

Length Optimization in Conformal Prediction

Conditional validity and length efficiency are two crucial aspects of conformal prediction (CP). Achieving conditional validity ensures accurate uncertainty quantification for data subpopulations, while proper length efficiency ensures that the prediction sets remain informative and non-trivial. Despite significant efforts to address each of these issues individually, a principled framework that reconciles these two objectives has been missing in the CP literature. In this paper, we develop Conformal Prediction with Length-Optimization (CPL) - a novel framework that constructs prediction sets with (near-) optimal length while ensuring conditional validity under various classes of covariate shifts, including the key cases of marginal and group-conditional coverage. In the infinite sample regime, we provide strong duality results which indicate that CPL achieves conditional validity and length optimality. In the finite sample regime, we show that CPL constructs conditionally valid prediction sets. Our extensive empirical evaluations demonstrate the superior prediction set size performance of CPL compared to state-of-the-art methods across diverse real-world and synthetic datasets in classification, regression, and text-related settings.

Conformal Prediction with Learned Features

In this paper, we focus on the problem of conformal prediction with conditional guarantees. Prior work has shown that it is impossible to construct nontrivial prediction sets with full conditional coverage guarantees. A wealth of research has considered relaxations of full conditional guarantees, relying on some predefined uncertainty structures. Departing from this line of thinking, we propose Partition Learning Conformal Prediction (PLCP), a framework to improve conditional validity of prediction sets through learning uncertainty-guided features from the calibration data. We implement PLCP efficiently with alternating gradient descent, utilizing off-the-shelf machine learning models. We further analyze PLCP theoretically and provide conditional guarantees for infinite and finite sample sizes. Finally, our experimental results over four real-world and synthetic datasets show the superior performance of PLCP compared to state-of-the-art methods in terms of coverage and length in both classification and regression scenarios.

Beyond the Universal Law of Robustness: Sharper Laws for Random Features and Neural Tangent Kernels

Machine learning models are vulnerable to adversarial perturbations, and a thought-provoking paper by Bubeck and Sellke has analyzed this phenomenon through the lens of over-parameterization: interpolating smoothly the data requires significantly more parameters than simply memorizing it. However, this "universal" law provides only a necessary condition for robustness, and it is unable to discriminate between models. In this paper, we address these gaps by focusing on empirical risk minimization in two prototypical settings, namely, random features and the neural tangent kernel (NTK). We prove that, for random features, the model is not robust for any degree of over-parameterization, even when the necessary condition coming from the universal law of robustness is satisfied. In contrast, for even activations, the NTK model meets the universal lower bound, and it is robust as soon as the necessary condition on over-parameterization is fulfilled. This also addresses a conjecture in prior work by Bubeck, Li and Nagaraj. Our analysis decouples the effect of the kernel of the model from an "interaction matrix", which describes the interaction with the test data and captures the effect of the activation. Our theoretical results are corroborated by numerical evidence on both synthetic and standard datasets (MNIST, CIFAR-10).

Sequential Estimation under Multiple Resources: a Bandit Point of View

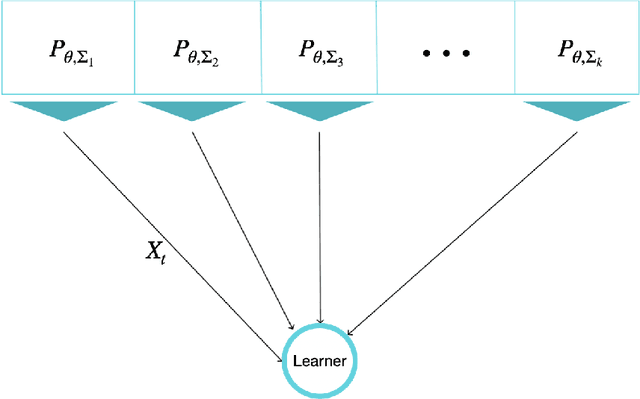
The problem of Sequential Estimation under Multiple Resources (SEMR) is defined in a federated setting. SEMR could be considered as the intersection of statistical estimation and bandit theory. In this problem, an agent is confronting with k resources to estimate a parameter $\theta$. The agent should continuously learn the quality of the resources by wisely choosing them and at the end, proposes an estimator based on the collected data. In this paper, we assume that the resources' distributions are Gaussian. The quality of the final estimator is evaluated by its mean squared error. Also, we restrict our class of estimators to unbiased estimators in order to define a meaningful notion of regret. The regret measures the performance of the agent by the variance of the final estimator in comparison to the optimal variance. We propose a lower bound to determine the fundamental limit of the setting even in the case that the distributions are not Gaussian. Also, we offer an order-optimal algorithm to achieve this lower bound.